News & Events
[알고리즘트레이딩/전략편] 09. 알고리즘 트레이딩 – 옵션의 페어트레이딩 (3)
- 2019년 1월 4일
- Posted by: 인사이트캠퍼스
- Category: 금융/AI/IT 기사

알고리즘 트레이딩 (Algorithmic Trading) – 전략 (9)
알고리즘 트레이딩 – 옵션의 페어트레이딩 (3)
“이 전략은 본 블로그의 페어 트레이딩 기초편 (1~9)의 사전지식을 요합니다.”
이전 2편의 포스트를 통해 옵션의 페어 트레이딩 전략에 대해 소개해 보았으나, 글로만 설명하는데 한계가 있어서 내용을 잘 표현하지 못하였다. 이번에는 수식을 통해 정밀하게 이 전략의 특성을 설명해 보고자 한다.
아래 그림은 행사가격이 277.5인 콜옵션 (C1)과, 행사가격이 280.0인 콜옵션 (C2)의 기초자산(S) 변화에 따른 가격 변화 그래프이다. 기초자산(S)를 289.0 인 지점으로 고정했을 때 C1=12.66 이고, C2=10.68 이다. 행사가격이 높을수록 행사될 가능성 (N[d2])이 낮아지므로 콜옵션의 가격은 낮아지고, 델타 값 (기울기)도 작아진다. S를 고정했을 때 두 옵션에 가격차 (C1 – C2)가 존재하고, 이 가격차는 행사확률에 따라 그 크기가 결정된다.
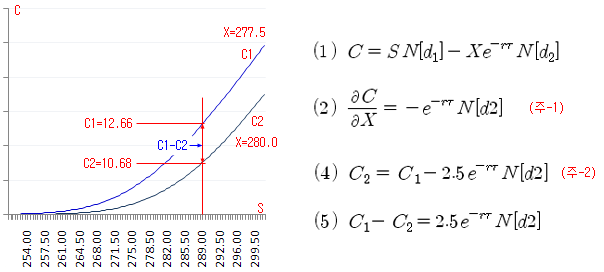
블랙-숄즈 옵션 공식을 사용하여 두 옵션의 가격차 (C1 – C2)를 계산해보자. 식 (1)은 블랙-숄즈의 옵션 공식이다. 식 (2)는 행사가격 변화에 따른 옵션가격의 민감도로, 행사가격이 1단위 변화했을 때 옵션가격의 변화량이다 (정확한 수식은 금융수학 편에서 계산할 것임. 주-1 참조). 이 민감도를 “Strike Delta” 라고 한다 (이름을 잘 몰랐었는데, 아래 덧들에 베이지안 님이 알려 주셨습니다).
민감도 Strike Delta를 이용하면 식 (4)와 같이 C2의 가격을 C1을 이용하여 표현할 수 있다. 식 (4)에서 C2의 가격은 C1의 가격에서 민감도의 2.5배 만큼 빼 준 것이 된다. 2.5배의 이유는 C1과 C2를 인접한 행사가격으로 선택했을 때, 인접한 행사가격은 2.5 포인트만큼 차이가 나기 때문이다 (280.0 – 277.5 = 2.5). 또한 Strike Delta는 1단위당으로 계산된 것이므로 2.5 포인트 당 변화는 2.5배의 Strike Delta가 될 것이다. 그렇다면 두 옵션의 가격차인 (C1 – C2)는 식 (5)와 같이 표현할 수 있다. 2.5배에 대한 상세 설명은 (주-1) 참조.
이전 포스트에서 옵션의 페어 트레이딩을 위한 스프레드는 두 옵션의 가격차 (C1 – C2)로 계산했었다. 그리고 그 스프레드가 기초자산 가격에 영향을 받아 움직이므로 페어 트레이딩이 가능하지 않았었다. 그 이유에 대한 명확한 설명이 식 (5)인 것이다. 식 (5)의 우변의 d2 항속에 S가 들어있으므로, S가 변함에 따라 (C1 – C2)가 변화는 것이고, 페어 트레이딩의 스프레드가 변하는 것이다 (스프레드가 S의 함수가 됨). 이 변화는 그래프를 보아도 설명이 된다.
안정된 스프레드를 만들려면, 식 (5)의 우변 항을 제거해야 한다. 그래야만 S에 무관한 스프레드를 만들 수 있고 시장중립전략 (Market Neutral Strategy)이 성립하게 된다. 아래에 식 (5)의 우변 항을 제거하는 2가지 방법을 소개해 본다.
1. 이론가를 이용하는 방법
이전 포스트에서 이론가를 고려한 스프레드에 대해 언급한 바 있다. 여기서 자세히 설명해 보면 아래와 같다.
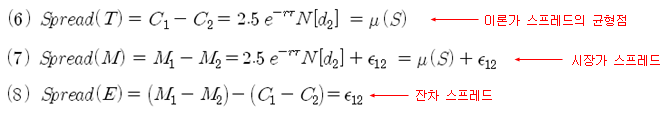
식 (6)은 식 (5)로 표현한 이론가의 가격차인, 이론가 스프레드이다. 이론가 스프레드는 u(S)로 표현하고, 이것을 페어 트레이딩의 균형점 (Long-run equilibrium)으로 해석할 수 있다. 왜냐하면 u(S)가 정상적인 가격차이므로 두 옵션의 가격차가 일시적으로 u(S)보다 크거나, 작게 벌어진다면 다시 u(S)로 회귀할 것이기 때문이다. 식 (7)은 옵션의 시장가에 대한 가격차인 시장가 스프레드이다. 시장가 스프레드도 식 (7)과 같이 균형점 u(S)와 잔차 스프레드로 나타낼 수 있다. u(S)는 기초자산 (S)의 함수이므로 S가 움직이는 방향에 따라 시장가 스프레드도 영향을 받아 같이 움직인다.
여기서 u(S)를 제거하면 식 (8)과 같이 된다. 즉, 식 (7)에서 식 (6)을 빼 주면 u(S)가 상쇄되고 잔차 스프레드만 남는다. 이것이 바로 이전 포스트에서 언급한 이론가를 고려한 스프레드이고, 기초자산의 변화에 무관한 스프레드이다. 이 스프레드의 활용에 대해서는 관심 있는 독자 분들의 도전을 기대 했었다.
2. 콜옵션 C3를 도입하는 방법
인접한 또 하나의 콜옵션인 C3를 도입하면 u(S)를 제거할 수 있다. 아래의 식 (9)는 행사가격-1 인 콜옵션 (M1)과 이보다 2.5포인트 큰 행사가격-2인 콜옵션 (M2)의 가격차이다. 식 (10)도 식 (9)와 동일한 의미로, 행사가격-2 인 콜옵션 (M2)과 2.5포인트 큰 행사가격-3인 콜옵션 (M3)의 가격차이다. 예를 들면, 행사가격-1은 277.5, 행사가격-2는 280.0, 행사가격-3은 282.5인 콜옵션이다.

식 (9)와 식 (10)에서 두 행사가격은 똑같이 2.5 포인트 차이가 나므로 u(S)도 비슷한 크기일 것이다 (완전히 동일하지는 않다). 따라서 식 (9)에서 식 (10)을 빼면 u(S)가 서로 상쇄될 것이고, 식 (11)과 같이 된다. 식 (11)을 정리하면 식 (12)가 되며, 잔차 성분만 갖는 스프레드가 될 수 있다. 식 (12)의 의미는 중간의 행사가격인 콜옵션 2계약을 매도하고, 양쪽으로 2.5포인트 차이가 나는 콜옵션을 각각 1계약씩 매수하면 u(S) 성분이 없고 잔차 성분만 갖는 포트폴리오를 구성할 수 있다는 것이다 (Butterfly Spread로 알려진 합성 전략이 된다).
식 (12)는 페어 트레이딩이라기보다는 행사가격 간 차익거래 (Strike Arbitrage)로 알려진 전략이다. 이 전략에 대해서는 이후 포스트에서 자세히 다루어 볼 예정이다.
(주-1)
1단위당 변화가 Strike Delta 이므로, 2.5 단위 (포인트) 변화 시에는 2.5를 곱해주어야 한다. 그러나 dC/dX에서 X가 미세하게 연속적으로 변해야 하므로, 곧바로 2.5를 곱해주는 것과는 약간의 차이가 난다. 여기서는 정확한 Strike Delta의 수치를 계산하는 것이 목적이 아니라, u(S)를 상쇄하는 것이 목적이므로, 간단히 2.5를 곱한 것으로 표현하였다.

