News & Events
[알고리즘트레이딩/전략편] 12. 옵션의 행사가격 차익거래 : Strike Arbitrage (1)
- 2019년 1월 4일
- Posted by: 인사이트캠퍼스
- Category: 금융/AI/IT 기사

알고리즘 트레이딩 (Algorithmic Trading) – 전략 (12)
옵션의 행사가격 차익거래 : Strike Arbitrage (1)
이번 시간에는 옵션의 행사가격별 차익거래 전략에 대해 살펴본다. 행사가격별로 옵션의 가격은 제각각이 아니라 공식처럼 정해져 있다. 행사가격이 X1인 옵션의 가치가 a 라면, 행사가격이 X2인 옵션은 a 와 밀접한 관계로 가격이 형성된다. 이것은 행사가격에 대한 옵션가격의 민감도로 설명된다 (행사가격 민감도의 자세한 내용은 금융수학/행사가 민감도 및 SPD 참조).
아래 그림은 기초자산 가격 (S)와 잔존기간 (T-t)가 일정할 때 행사가격별 콜옵션의 가격을 그린 것이다 (그리는 방법은 블랙숄즈 공식의 활용 : 엑셀계산 참조). 왼쪽 그림은 행사가격의 범위가 240.0 ~ 300.0 까지 일 때 콜옵션의 가격변화를 그린 것이다. 행사가격이 높아질수록 행사 가능성이 낮아지므로 콜옵션의 가격은 내려간다. 그림의 왼쪽 영역은 내가격 (In the money)에 있는 옵션들이고, 오른쪽 영역은 외가격 (Out of the money)에 있는 옵션들이다. 기초자산 가격 근처의 영역은 등가격 (At the money 혹은 Near the money)에 있는 옵션들이다. 그림과 같이 각 옵션들은 일정한 규칙 하에 가격이 형성되고 있다. 풋옵션의 경우는 그림의 방향만 반대이고 규칙성은 동일하다.
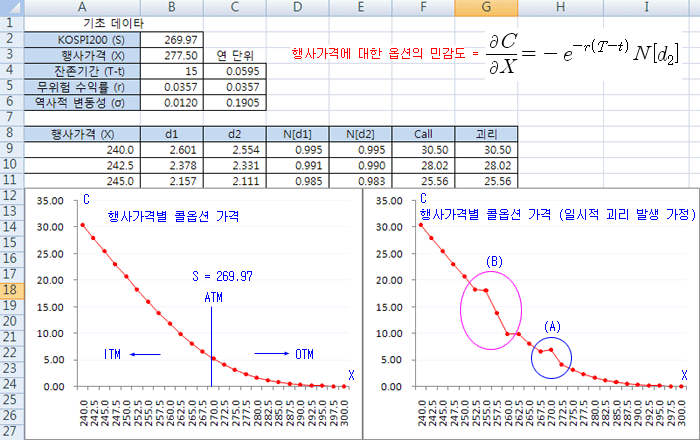
만약 특정 행사가격의 옵션이 오른쪽 그림과 같이 정상적인 궤도를 일시적으로 벗어난다면 차익거래 기회가 발생한다. 예를 들어 오른쪽 그림과 같이 순간적으로 괴리가 발생했다고 가정해 보자. 현실에서는 이렇게 눈에 띌 정도의 괴리는 발생하지 않는다. 여기서는 설명을 위해 다소 과장하여 그려 놓은 것이다. 그림을 보면 3 군데 행사가격의 옵션이 궤도를 벗어났다. (A) 영역의 가운데 옵션은 궤도보다 위에 있고, (B) 영역의 두 번째는 궤도보다 위에, 네 번째는 아래에 있다. 알고리즘 트레이딩으로 이와 같은 괴리가 포착되었다면 주변의 옵션을 이용하여 여러 가지 방법 (조합)으로 차익거래 실현을 생각해 볼 수 있다.
여러 가지 조합 중에 아래 그림의 두 가지 경우를 생각해 보자. 왼쪽의 삼각형은 (A) 영역을 확대해 본 것이다. 행사가격이 X1, X2, X3가 있을 때 X2가 궤도를 벗어난 경우이다. 포지션 계산을 위해 옵션의 가격을 그림과 같이 가정해 보자. 정상 궤도인 경우 행사가격이 X3인 옵션의 가격은 5이고, 나머지는 7.5와 10이라고 가정한다. 그러면 큰 삼각형과 작은 삼각형이 닮은꼴이므로 간단한 비례식으로 포지션을 계산할 수 있다. 실제로 X2의 옵션가격은 삼각형의 빗변보다 약간 아래에 위치하지만 (위의 그림에서 가격변화는 곡선이므로), 계산을 위해 삼각형으로 근사시켜 생각해 본 것이다.
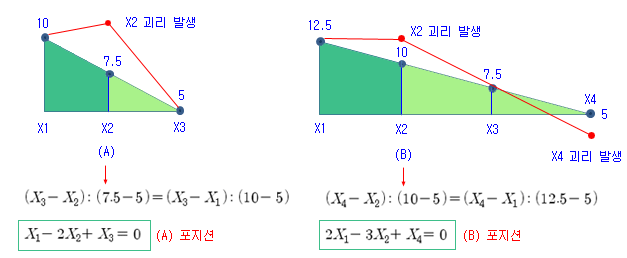
비례식을 쓰면 (A)의 경우는 X1 – 2*X2 + X3 = 0 이 나온다. 이 식이 정상 궤도의 식이다. 이 식의 의미는 행사가격이 X1인 옵션을 1계약 매수하고, X2는 2계약 매도, X3을 1계약 매수하면 정상 상태가 된다는 의미이다 (만기 시 기댓값이 0인 상태). 만약 X2가 그림과 같이 정상 궤도를 벗어난 경우, 포지션 (A)를 구축한 후에 X2가 정상으로 회귀할 때 반대로 매매하면 이론적으로는 X2의 괴리만큼 차익을 얻을 수 있다 (거래 비용을 고려하지 않은 경우)..
(B)의 경우도 동일한 방식으로 포지션을 계산해 보면, 위의 그림과 같은 식이 되고, X1을 2계약 매수, X2는 3계약 매도, X4는 1계약 매수하면 X2와 X4의 괴리만큼의 차익을 동시에 얻을 수 있다.
만약에 포지션 (A)와 (B)를 만기 시 까지 보유한다면, 좌변이 0 보다 크거나 같으면 무위험 차익거래가 되고, 좌변이 0보다 작으면 수익이 날 수도 있고, 손실이 날 수도 있는 통계적 차익거래가 된다. 이 관계를 알아보기 위해 필자가 제작한 합성옵션계산기로 손익구조를 분석해 보면 아래와 같이 된다.

위의 왼쪽 그림은 포지션 (A)의 만기 손익 (Pay-off)이고 (정확히 만기는 아니고 잔존기간이 약간 남게 그림을 그렸다), 오른쪽 그림은 포지션 (B)의 만기 손익이다. 모두 버터플라이라는 옵션의 합성전략이 된다. 두 경우 모두 좌변이 0 보다 크거나 작다면 만기 시 기초자산의 가격과는 무관하게 손실 구간이 없는 완전한 무위험 차익거래가 된다. 만약 알고리즘으로 무위험 차익거래 기회가 포착되면 반대 매매로 청산하는 것이 아니라 계속 누적해서 포지션을 진입해 놓으면 된다. 그러면 만기 시 절대수익이 보장되어 있으므로, 청산 시 발생하는 거래 비용이 절감된다. 그러나 현실에서는 무위험 차익거래 기회는 발생하기 어렵다. 단, 깊은 외가격이나 내가격에서는 자주 발생하기도 하지만 거래량이 작아 포지션 진입이 어렵다 (아직 연구 대상이다).
만약 좌변이 0 보다 작으면, 만기 시 기초자산 가격에 의해 수익구간이 되기도 하고 손실구간이 되기도 한다. 좌변이 0 에 근접한 값으로 진입하였다면 만기 시 기댓값이 커질 수 있으므로, 통계적 차익거래가 된다.
이 전략에 대해서는 통일된 매매 시나리오를 작성하기는 어렵다. 그 이유는 기회가 포착되었을 때 포지션 진입을 위한 구성이 다양하기 때문이다. 맨 위의 괴리가 발생한 그림에서 괴리가 발생한 영역인 (A)와 (B)에 대해 위에서 설명한 것과는 다른 조합으로 포지션을 구축할 수도 있다. 예를 들어 (A)와 (B)사이에 있는 옵션들로 포지션 조합을 구성할 수도 있기 때문에 최적의 진입 포지션을 찾는 시나리오가 필요할 수도 있다. 따라서 여기서는 자동매매 절차 시나리오는 없이 기회만 포착하는 로봇을 돌려서 로그 파일을 통해 현실에서 차익거래 기회가 얼마나 발생하고 있는지에 대해서만 분석해 보도록 하겠다.
자동 매매 시나리오는 독자 분들의 창의성을 기대하며, 로그 파일 분석결과는 다음 포스트에서 살펴보도록 한다.

