[금융수학] 11. 금융공학 – 마팅게일 (Martingale)

금융 수학 (11)

금융공학 – 마팅게일 (Martingale)

이전 포스트에서는 위험중립확률을 통한 게임의 공정성에 대해 알아보았다. 게임 혹은 금융에서 공정성이라고 하는 것은 대단히 중요한 개념이다. 금융시장이 불공정해진다면 시장 참여자들이 줄어들 것이고, 시장은 존재하기 어렵게 된다. 시장은 다수의 참여자에 의해 스스로 공정성을 유지하는 힘을 가지고 있다. 시장의 공정성에 대해서는 위험중립확률 (Risk Neutral Probability), 효율적시장가설 (EMH : Effective Market Hypothesis) 등으로 설명할 수 있지만, 더 구체적인 표현으로는 금융공학의 마팅게일 (Martingale) 이라는 개념이 사용된다.

마팅게일은 금융자산의 가격이나, 시장의 공정성에 관한 구체적 표현으로, 어느 참여자도 불만을 갖지 않는 상태를 의미한다. 바둑에서 정석이란 상대방을 이기기 위한 전략이 아니라, 흑, 백 간에 서로 불만이 없고, 균형을 이룬 상태를 말한다. 흑이나 백 중에 어느 한 쪽에만 유리한 전략이라면 정석으로 채택될 수 없을 것이다 (이런 전략이 있을 수도 없다). 금융시장에도 정석이 존재한다면 아마도 마팅게일이 가장 유력할 것으로 생각된다.

재무관리에서는 차익거래 조건하에서 금융자산의 공정한 가격을 산출한다. 마찬가지 개념으로 금융공학에서는 마팅게일 조건하에서 금융자산의 공정가격을 산출한다. 따라서 마팅게일은 금융공학에서 대단히 중요한 위치를 차지하고 있다.

효율적시장가설이나 마팅게일을 확률적 시각에서만 보면, 절대로 초과수익을 낼 수 없다는 다소 비관적인 의미로 해석될 수도 있다. 그러나 시장에는 분명히 수익을 내는 투자자가 있고, 손실을 보는 투자자가 있다. 이 들을 모두 통틀어 보았을 때 공정한 상태가 된다는 의미일 것이다. 큰 위험을 지불한 투자자는 큰 수익을 기대할 수 있고, 반면에 큰 손실을 볼 수도 있다. 시간이나 노력을 많이 지불한 투자자는 조금 더 그 대가를 기대할 수도 있다. 확실한 것은, 남들은 모르고 나만 아는 전략으로 큰 수익을 올릴 수 있다는 기대는 큰 착각이고 탐욕이라는 것이다. 그 이유는 바로 마팅게일에 위배되기 때문이다.

마팅게일에 대해 너무 크게 포장한 것 같은데 (필자가 너무 중요하게 생각하는 개념이기 때문), 이제는 좀 작지만 구체적으로 접근해 보도록 하자. 아래 그림은 이전 포스트에서 살펴본 그림이다. 이것이 위험중립확률로 만들어진 과정이라면, 이 게임은 공정한 게임이 될 것이고, 1기의 (1회 시행) 기댓값은 이전 기의 원금과 같아질 것이다.

이전 포스트에서 계산한데로 아래 그림은 승률이 1/3인 위험중립확률을 가진다. 게임을 1회 시행했을 때의 기댓값은 8로 원금인 8과 동일하다. 이것을 수식으로 표현하면 식 (1)과 같이 된다. 식 (2)는 식 (1)을 조건부 확률로 표시한 것이고, 그 의미는 0-기에 원금이 8인 것을 알고 있는 상태에서 (F0), 1-기의 (S1) 기댓값은 8이라는 것이다. 식 (4)는 2-기의 값이 32일 때 (F2=32), 4-기의 기댓값은 32라는 것을 의미한다. 즉 4-기의 기댓값은 F2의 값과 같아진다 (실제 기댓값을 계산해 보면 32가 나온다).

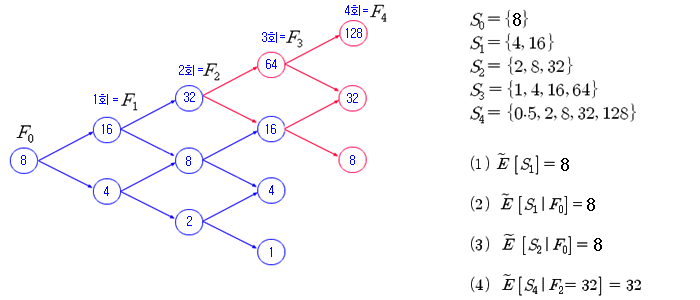
위의 관계를 일반적으로 나타내면 아래와 같이 표현할 수 있다. 식 (5)의 물결무늬는 위험중립확률이 사용되었음을 의미한다. k-기의 값을 알고 있을 때 (Fk), l-기의 기댓값은, k-기의 값과 같다는 의미이다. 식 (6)은 실제 확률을 사용한 표현이다 (물결무늬가 없음). 이것이 바로 마팅게일의 수학적 표현이다.

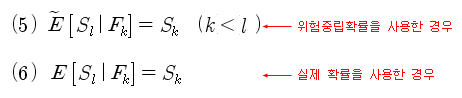
공정한 게임이라면 식 (5)나 (6)이 항상 성립한다. 반대로 어떤 게임이나 확률과정이 식 (5)나 (6)의 성질을 만족한다면 그 게임은 공정하다고 판단할 수 있다. 즉 어떤 확률과정에 대해 마팅게일의 성질을 만족하는지 확인해 보면, 그 확률과정이 공정한 것인지 아닌지 확인해 볼 수 있다.

아래의 그림은 랜덤 워크 (Random Walk) 과정이다. 랜덤 워크 과정은 공정한 확률과정일까? 이 과정에 투자한다면 기대수익률은 얼마가 될까? 이러한 질문에 대한 답은, 이 과정의 마팅게일 성질을 확인해 보면 알 수 있다. 식 (7)은 식 (6)의 좌변을 표시한 것이고, 이 식을 아래와 같이 변형해 보면 5번째 식인 Mk가 된다. Mk는 식 (6)의 우변이므로, 이 과정은 마팅게일이라는 것을 알 수 있다, 식 (8). 즉 랜덤 워크는 공정한 확률과정이며, 기대수익률은 0 이라는 것을 알 수 있다.

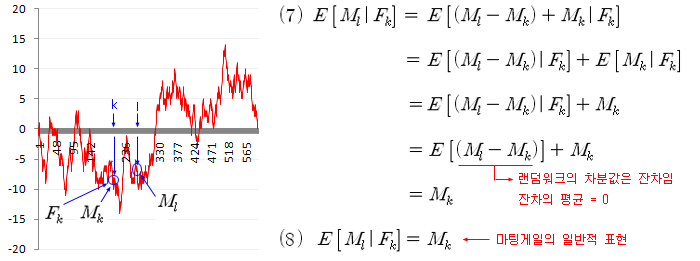
위의 식에서, 첫 번째 식은 Mk를 한 번씩 더하고 뺀 것이고, 두 번째 ~ 네 번째 식은 조건부 확률의 일반적인 성질이다. 두 번째 식에서 E[Mk | Fk] 는 k-번째로 이미 알려져 있는 값이므로 기댓값은 Mk가 된다. 네 번째 식에서 Ml – Mk는 랜덤 워크의 특성으로 0 이 된다.

위와 동일한 방법으로 계산해 보면, 기하 브라운 운동이나 위너 과정도 모두 마팅게일의 성질을 만족한다. 주가 모형도 위너 과정에 기초하고 있으므로 마팅게일의 성질을 만족한다. 그러면 주가도 마팅게일 과정이고 공정한 확률 과정이라 할 수 있다.

마팅게일 과정은 기댓값이 초기값 (투자금)과 같다. 만약 기댓값이 투자금보다 크다면 투자자에게 유리한 과정이 되고, 이러한 과정을 서브 마팅게일 (Sub Martingale)이라 한다. 반대로 기댓값이 투자금보다 작으면 투자자에게 불리한 과정이 되고, 슈퍼 마팅게일 (Super Martingale)이라 한다.

주식시장은 마팅게일 인가?

좁게 보면, 주식시장은 거래 수수료와 거래 세금이 존재하므로 기댓값이 투자금보다 작은 슈퍼 마팅게일로 볼 수도 있다. 그러나 넓게 보면 거래 수수료를 받는 증권사는 거래를 위한 시설투자비용, 유지보수비용, 운용비용 등을 지출해야 하므로 일반 투자자와 대등한 입장일 것이다. 또한, 거래 세금을 징수하는 정부는 경제 상황에 따라 금융정책이나 재정정책 등을 통해 주가 부양정책 같은 것을 쓸 때 지출이 발생하므로 마찬가지 상황일 것이다 (물론, 규모의 차이가 발생할 수는 있다). 따라서 금융공학적으로 보면 주식시장은 역시 마팅게일 (Martingale)이 아닌가 생각해 본다.

[출처]11. 금융공학 – 마팅게일 (Martingale)|작성자아마퀀트