[금융수학] 13. 금융수학 – 블랙숄즈 옵션공식의 미분 방법

금융 수학 (13)

금융수학 – 블랙숄즈 옵션공식의 미분 방법

옵션의 전략 개발을 위해 수리적 모형을 만들거나, Greeks에 대한 식을 만들 때 등 블랙숄즈 공식을 미분해야할 경우가 많이 있다. Greeks의 경우에는 일반 옵션 투자자들도 기본적으로 많이 알고 있는 사항이다. 공식 자체는 잘 모를 수 있으나 그 의미와 활용에 대해서는 전문가 수준으로 많이 알고 있다. 여기서는 이러한 공식을 직접 유도해 보기위해 필요한 사전지식을 익혀 보고자 한다.

예를 들어 기초자산 가격 변화나, 시간 변화에 대해 콜옵션 가격이 어떻게 변화하는지 알아보려면 콜옵션 공식을 기초자산 가격이나 시간에 대해 미분해서 그 값이 어떻게 변하는지 확인해 보아야한다. 이러한 계산을 자유자재로 하기위해서는 블랙숄즈 공식을 자유자재로 미분할 수 있어야 한다.

블랙숄즈 공식은 그 형태가 누적확률분포 형태, 적분형태 등으로 표현되어 있어, 그 형태가 다소 복잡해 보인다. 복잡한 식을 사전지식 없이 미분하려고 시도해 보면 첫 스텝부터 막히는 경우를 경험하게 된다. 여기서 다루는 기본지식을 알고 나면 비교적 쉽게 미분이 풀려나간다.

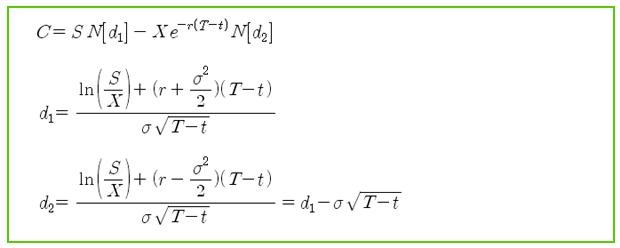
위의 식은 블랙숄즈 공식이다. 위의 식에 대해 기본적으로 필요한 몇 가지를 미리 미분해 놓도록 한다.

1. N[d1]의 미분 방법

N[d1]은 표준정규분포인 누적확률밀도함수의 표현으로 식 (1)로 정의된 표현이다. 식 (1)은 적분형태를 취하므로, 이를 d1에 대해 미분하면 적분과 상쇄되어 간단히 식 (2)와 같이 된다. 간단히 N'[d1]으로 표기 한다.

2. d1 의 미분 방법

d1은 식 (3)으로 정의된 식이므로, 이를 시간 t로 미분하면 식 (5)와 같이 된다. 또한, d1을 기초자산인 S로 미분하면 식 (6)이 되고, 변동성인 시그마로 미분하면 식 (8)이 된다. 미적분학의 기본이론을 사용하여 단순히 미분만 하면 된다. d2에 대한 미분은 d1의 미분 식을 이용하면 쉽게 표시할 수 있다.

3. N[d1], N[d2]의 다양한 미분 방법

위의 기본식을 이용하면, N[d1], N[d2]의 다양한 미분을 쉽게 할 수 있다. 예를 들어 N[d1]을 S에 대해 미분하려면 식 (9)와 같이 Chain rule을 써서 쉽게 미분할 수 있다. N[d2]의 경우도 d1의 미분을 이용하면 식 (10) ~ (11)과 같이 쉽게 미분할 수 있다.

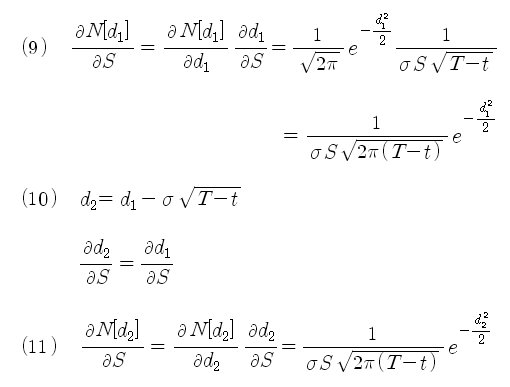
식 (9)와 식 (11)은 이미 옵션의 페어 트레이딩 전략(4) 편에서 이미 활용한 적이 있다. 위의 기본식 들은 옵션의 전략을 만들거나, Greeks 등의 공식을 만들 때 매우 유용하게 사용된다.

이번 포스트는 다소 지루한 면이 있으나, Greeks 계산이나, 향후 알고리즘 트레이딩의 전략을 개발할 때 아주 빈번히 참조될 중요한 포스트 중에 하나이다.

[출처]13. 금융수학 – 블랙숄즈 옵션공식의 미분 방법|작성자아마퀀트