[금융수학] 14. 금융수학 – 옵션의 델타 공식 유도과정 (Greeks : Delta)

금융 수학 (14)

금융수학 – 옵션의 델타 공식 유도과정 (Greeks : Delta)

옵션의 델타 (Delta)는 기초자산(S)의 가격변화에 대한 옵션가격의 변화량을 말한다. 옵션 가격의 민감도라고도 한다. 다시 말하면 기초자산 가격이 1 만큼 증가하였을 때 옵션의 가격은 얼마나 변화하는가를 나타내는 척도이다.

아래 그림은 블랙숄즈 공식의 활용편에서 계산해본 콜옵션의 가격변화 그래프이다. 옵션의 델타는 그림과 같이 옵션가격 그래프의 기울기로 해석된다. 기초자산 가격이 S1=273일 때의 기울기보다, S2=288일 때의 기울기가 더 크다. 이것은 기초자산 가격이 상승할수록 콜옵션의 가격은 더 급하게 상승한다는 의미이다. 기초자산 가격이 충분히 커지면 옵션의 가격은 직선에 가까워지므로 기울기는 어느 정도 일정해 진다. 오른쪽 그림은 기초자산 가격(S) 대 델타의 그래프이다. S가 증가할수록 델타가 점점 증가하다가 S가 충분히 커지면 델타는 점차 일정해지는 S-자 곡선을 보이고 있다.

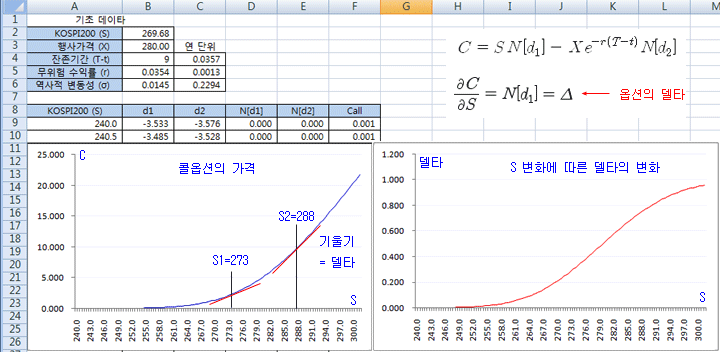
옵션의 델타는 옵션투자에서 가장 중요한 의미를 가지는 요소일 것이다. 델타는 블랙 숄즈 옵션공식을 만들 때부터 이미 기초자산의 헤지 비율로 사용되었다. 따라서 델타는 헤지와 많은 관련이 있다 (델타 헤지). 위의 그림에서 델타값이 N[d1]이고, N[d1]은 항상 0~1 사이의 값이므로 델타는 기초자산 가격의 증가보다는 항상 작게 된다. 예를 들어 기초자산이 1 증가하였을 때 델타가 0.4라면, 기초자산이 100원 오르면, 옵션은 40원 오른다는 의미이다. 그러므로 기초자산과 옵션으로 구성된 포트폴리오가 있다면 옵션의 헤지비율은 항상 1보다 크게 된다 (옵션의 투자비율이 더 높아야 한다).

콜옵션의 델타는 기초자산이 증가하면 같이 증가하므로 양 (+)의 값을 가지고, 풋옵션의 델타는 반대 방향이므로 음 (-)의 값을 가진다.

이제 델타의 공식을 직접 유도해 보기로 하자. 블랙숄즈 옵션공식의 미분 방법을 다룬 포스트에서 기본적인 부분을 미리 미분해 놓았기 때문에 이를 이용하면 어렵지 않게 델타 공식을 유도할 수 있다. 델타를 구하려면 블랙 숄즈 공식을 S로 편미분해야 하는데, 각 항의 d1, d2 가 모두 S에 대한 함수이므로 이를 모두 고려해서 편미분해 주어야 한다.

* 옵션 델타의 유도과정

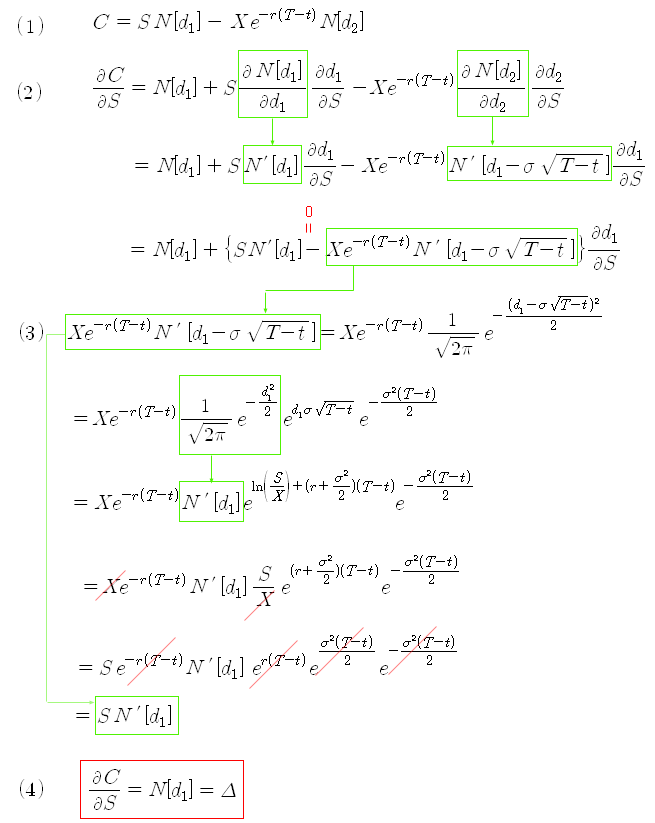
풋옵션의 델타는 풋-콜 페리티 식으로부터 아래와 같이 구하면 된다.

[출처]14. 금융수학 – 옵션의 델타 공식 유도과정 (Greeks : Delta)|작성자아마퀀트