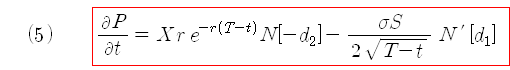News & Events
[금융수학] 15. 옵션의 시간가치 엑셀계산 및 세타 공식 유도과정 (Greeks : Theta)
금융 수학 (15)
옵션의 시간가치 엑셀계산 및 세타 공식 유도과정 (Greeks : Theta)
옵션의 세타 (Theta)는 시간의 변화 (잔존기간)에 따른 옵션가격의 변화량으로, 시간이 1단위 증가했을 때 경과했을 때 옵션의 가격은 얼마나 변화하는가를 나타내는 척도이다. 이 변화량을 시간가치라 하고 시간이 증가할수록 시간가치가 감소하기 때문에 옵션의 가치도 감소한다.
아래 그림은 블랙숄즈 공식의 활용 (엑셀계산)편에서 계산해본 콜옵션의 가격변화 그래프에 시간가치 (세타) 계산을 추가한 것이다. 왼쪽 그래프에서 기초자산 (S)의 가격이 같을 때, 잔존기간이 15일 남은 콜옵션의 가치가 잔존기간이 2일 남은 콜옵션의 가치보다 더 크다. 이것은 S가 동일하여도 잔존기간이 많이 남을수록 시간가치가 커지기 때문이디. 잔존기간이 많이 남았다는 것은 앞으로 얼마든지 행사될 가능성이 있으므로 시간에 대한 가치가 발생한다. 잔존기간이 조금밖에 남지 않았다면 행사될 가능성이 줄어들기 때문에 시간가치도 줄어들 수밖에 없다.
오른쪽 그림은 잔존기간은 고정된 상태에서 기초자산 가격이 변할 때 세타의 변화를 그린 것이다. 옵션의 세타는 시간에 따라 감소하기 때문에 세타는 음 (-)의 값을 가진다. S가 증가할수록 시간가치 감소량이 커지다가 행사가격 부근에서 최대가 되고, 그 이후로는 다시 감소폭이 작아진다 (등가격 : ATM에서 시간가치 감소폭이 최대가 된다).
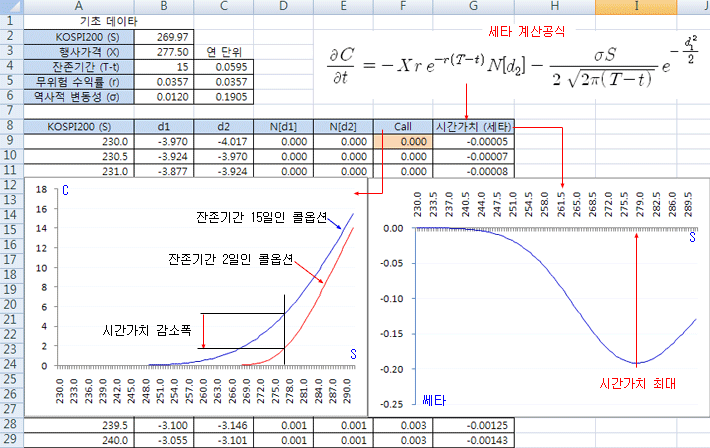
위 그림에 세타를 계산하는 공식을 표시하였다. 델타에 비해 다소 복잡한 형태를 보인다. 시간가치는 옵션이 행사될 가능성과 관계가 있으므로, 공식에 행사확률인 N[d2]가 관계되어 있다. 이 식으로 계산한 결과는 연단위의 시간가치이므로 (잔존기간 등 모든 변수를 연단위로 계산하였으므로) 일일 단위의 시간가치를 구할 때는 252로 나누어 주어야 한다 (연단위를 365로 계산하였으면 365로 나누어 준다).
엑셀에서 각 셀의 계산식은 아래와 같다.
* 잔존기간 : 셀(C4) = B4 / 252
d1 : 셀(B9) = (LN(A9/$B$3)+($C$5+($C$6^2)/2)*$C$4)/($C$6*SQRT($C$4))
d2 : 셀(C9) = B9-$C$6*SQRT($C$4)
N[d1] : 셀(D9) = NORMSDIST(B9)
N[d2] : 셀(E9) = NORMSDIST(C9)
Call 가격 : 셀(F9) = A9*D9-$B$3*EXP(-$C$5*$C$4)*E9
세타 : 셀(G9) = (-$B$3*$C$5*EXP(-$C$5*$C$4)*E9
-($C$6*A9/(2*SQRT(2*3.1416*$C$4)))*EXP(-(B9^2)/2)) / 252
일일 단위의 세타가 0.12라면 기초자산 가격의 변화가 없을 때 옵션의 가치는 하루에 0.12만큼 감소한다는 의미이다. 옵션 거래단위의 1 Tick이 0.01 포인트이므로 시간가치는 12 Tick에 해당한다. 즉, 옵션을 매수한 상태에서 기초자산 가격의 변화가 전혀 없어도 옵션의 가격은 12 Tick 만큼 하락하여 손실을 보게 된다. 이것이 시간가치의 감소 효과이다. 반대로 옵션을 매도한 상태라면 12 Tick 만큼의 이익을 보게 된다. 따라서 옵션을 매수하여 1일간 보유한다는 것은 기초자산의 일일 가격변동성이 최소한 12 Tick 이상이 될 것으로 기대한다는 의미인 것이다 (매도의 경우는 반대이다).
만약 시간가치가 관련된 전략을 알고리즘 트레이딩으로 구현할 때에는 일일 중 시간가치를 연속적으로 감소시켜 주어야 한다. 1일 시간가치가 0.12라는 의미는 24시간 동안 감소한다는 것은 아닐 것이다. 1일 중 옵션의 거래시간은 6시간이므로 6시간 만에 0.12가 감소하는 것으로 보아야 타당하다. 즉 시간당 2 Tick의 시간가치 감소가 일어난다. 만약 거래개시 시각인 09:00 현재 당일의 시간가치가 0.12로 예상되었다면, 10:00 현재에는 이미 2 Tick이 감소되어 오늘 남은 시간가치 하락폭은 0.10 이 된다. 알고리즘 트레이딩에서는 이를 실시간으로 감소시켜 주어야 정확한 계산이 될 것이다. 큰 차이가 아닐 수도 있지만 알고리즘 트레이딩은 1 ~ 2 Tick을 가지고 경쟁하는 경우가 많으므로 이 효과를 고려해 주어야 한다. 글로 표현하기가 어려워 필자가 만든 프로그램의 일부 코드를 아래에 첨부해 보았다 (주석 참조).
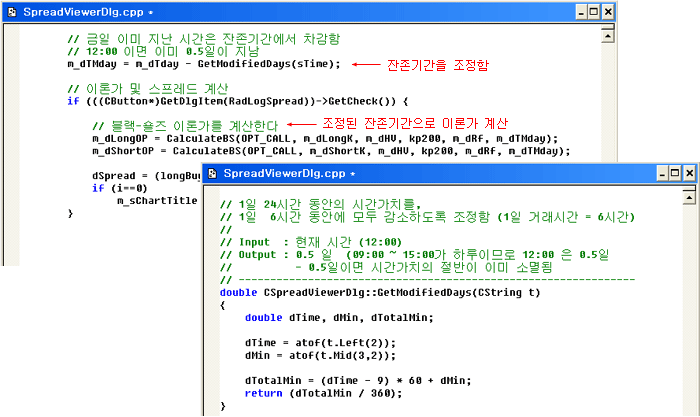
이제 세타의 공식을 직접 유도해 보기로 하자. 델타공식 유도와 마찬가지로 블랙숄즈 옵션공식의 미분 방법을 다룬 포스트에서 기본적인 부분을 미리 미분해 놓았기 때문에 이를 이용하면 어렵지 않게 공식을 유도할 수 있다. 세타는 시간에 따른 옵션가격의 변화량이므로 블랙 숄즈 공식의 각 항을 시간 (t)에 대해 편미분해 준다.
* 옵션 세타의 유도과정
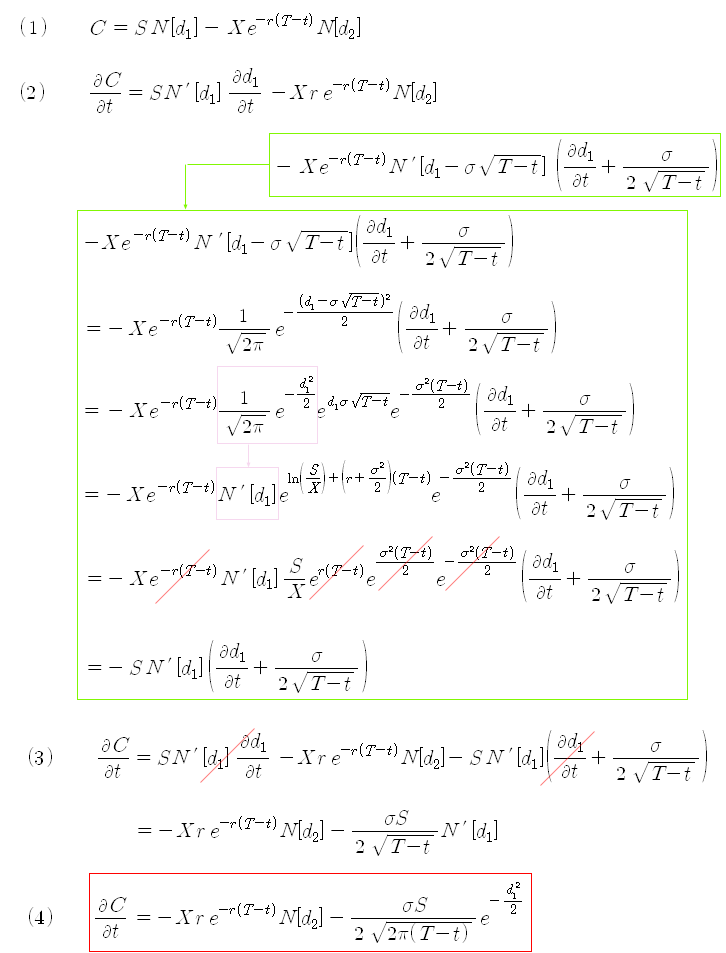
풋옵션의 세타도 풋-콜 페리티를 이용하여 계산하면 아래와 같이 된다.
