News & Events
[금융수학] 17. 옵션의 베가 엑셀계산 및 공식 유도과정 (Greeks : Vega)
금융 수학 (17)
옵션의 베가 엑셀계산 및 공식 유도과정 (Greeks : Vega)
옵션의 베가 (Vega)는 기초자산의 변동성 변화에 따른 옵션가격의 변화량으로, 옵션가격을 변동성으로 편미분한 값이다. 즉 기초자산의 변동성이 1% 변할 때 옵션의 가격은 얼마큼 변하는가를 나타낸다. 기초자산의 변동성이 증가하면 옵션이 행사될 기대가 높아지므로 옵션의 가격은 상승하게 된다.
아래 그림은 엑셀에서, 기초자산의 가격이 240.0 ~ 300.0 까지 변할 때, 베가값을 계산한 것이고, 세타와 관련이 많으므로 세타도 같이 계산해 보았다. 기초자산 가격이 상승하면 베가도 상승하다가, 기초자산 가격이 행사가격을 지나면서 다시 감소하고 있다. 따라서 베가는 옵션의 행사가격 (ATM) 지점에서 최대가 된다. 세타의 변화도 방향만 반대일 뿐 성질은 동일하다. 기초자산 가격이 상승하면 세타는 음 (-)의 방향으로 증가하다가, ATM에서 최대 (음의 방향으로)가 되고, 이후로 다시 감소하고 있다.
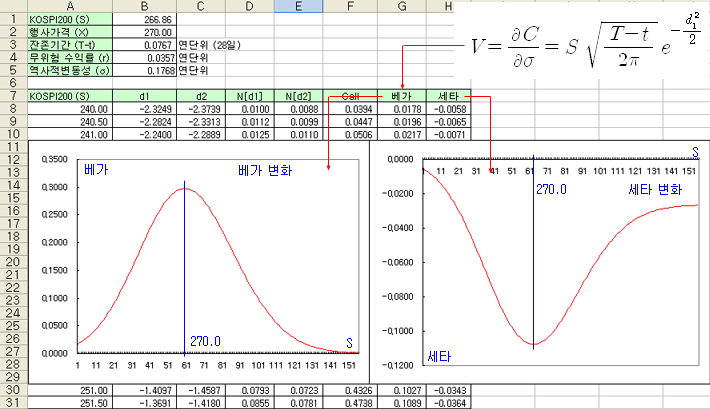
ATM에서 베가가 최대가 되고, ATM이 기초자산의 변동성에 가장 민감한 지점이 된다. 기초자산의 변동성이 증가할 것으로 예상되는 경우, ATM의 옵션을 매수하면 베가가 최대이므로, 수익도 최대가 될 것이다. 반면에 ATM에서는 세타도 최대이므로, ATM의 옵션을 매수하면 가장 큰 시간가치를 지불해야 한다. 따라서 ATM의 옵션을 매수한다는 것은 가장 큰 시간가치를 대가로 지불하고, 가장 큰 변동성 이익을 취하겠다는 의미가 된다. 예상대로 변동성이 증가한다면 수익은 최대가 되고, 예측이 빗나간다면 손실도 최대가 되는 것이다. 마찬가지로 ITM이나, OTM에서는 작은 시간가치를 지불하고, 작은 변동성 수익을 취한다는 의미도 된다.
옵션의 매수자 입장에서는 베가는 크고, 세타는 작은 행사가격이 유리한데, 이런 지점이 존재할까? 그렇지 않다. 매수자는 베가대 세타 비율 (베가/세타)이 큰 값을 원하겠지만, 위의 그래프를 보면 베가가 커지면 세타도 같이 커지므로 (절대값으로 비교) 베가대 세타의 비율은 항상 일정하게 유지 된다. 따라서 어는 행사가격이라도 큰 베가를 얻으려면 큰 세타를 지불해야하고, 작은 세타를 지불하려면 베가도 작게 얻을 수밖에 없게 된다.
현재 KOSPI200 지수는 265.27 이고 행사가격이 267.50인 콜옵션의 현재가는 3.60 이다. 베가는 0.2750이고, 세타는 -0.1086이다. KOSPI200이 1% 상승하여 270.18이 되면, 콜옵션의 가격은 3.60 + 0.2750 = 3.875가 된다. 그러면 기초자산이 1% 상승하면 콜옵션은 7% 상승하는 것이 된다 (레버리지 효과). 이것이 베가의 의미이다. 세타는 하루 동안 0.1086을 시간가치로 지불해야 한다. 이것을 %로 환산해 보면 약 3%가 된다 (0.1086 / 3.60).
엑셀에서 각 셀의 계산식은 아래와 같다.
* d1 : 셀(B8) = (LN(A8/$B$2)+($B$+($B$5^2)/2)*$B$3)/($B$5*SQRT($B$3))
d2 : 셀(C8) = B8-$B$5*SQRT($B$3)
N[d1] : 셀(D8) = NORMSDIST(B8)
N[d2] : 셀(E8) = NORMSDIST(C8)
Call 가격 : 셀(F8) = A8*D8-$B$2*EXP(-$B$4*$B$3)*E8
베가 : 셀(G8) = (EXP(-(B8^2)/2)/($B$5*A8*SQRT(2*3.1416*$B$3))) / 100
세타 : 셀(H8) = (-$B$2*$B$4*EXP(-$B$4*$B$3)*E8-$B$5*A8*EXP(-(B8^2)/2) /
(2*SQRT(2*3.1416*$B$3))) / 365
* 변동성의 단위가 %이므로, 베가의 결과값을 100으로 나누어 주어야한다.
* 세타의 결과값은 연간 단위이므로, 365로 나누어서 일단위로 환산해 준 것이다.
* 나머지 셀은 “블랙숄즈 공식의 활용 – 엑셀 연습” 참조
* 옵션 베가의 유도과정 (블랙숄즈 옵션 공식의 미분방법 참조)
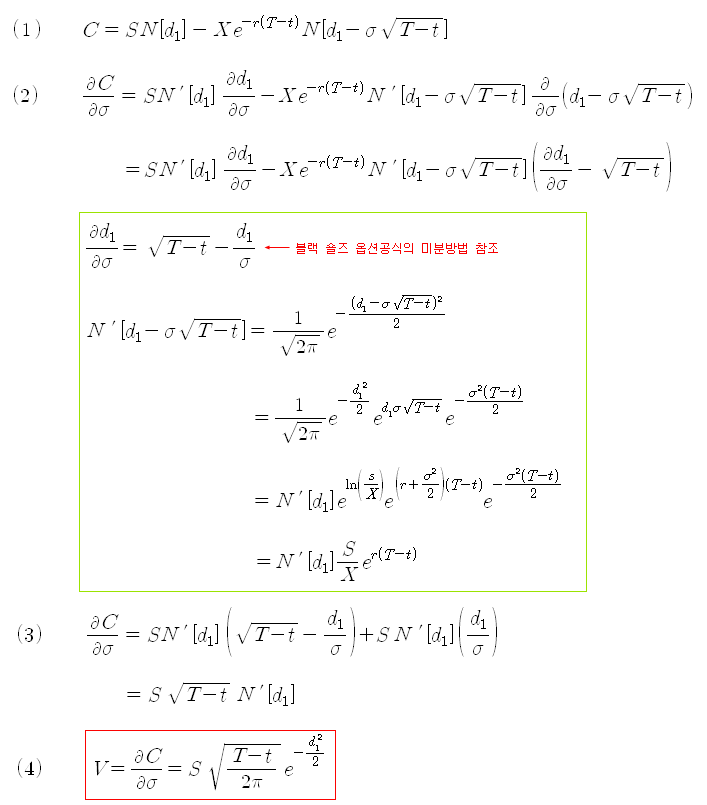
풋옵션의 베가는 풋-콜 페리티를 이용하면 콜옵션의 베가와 동일함을 알 수 있다.
