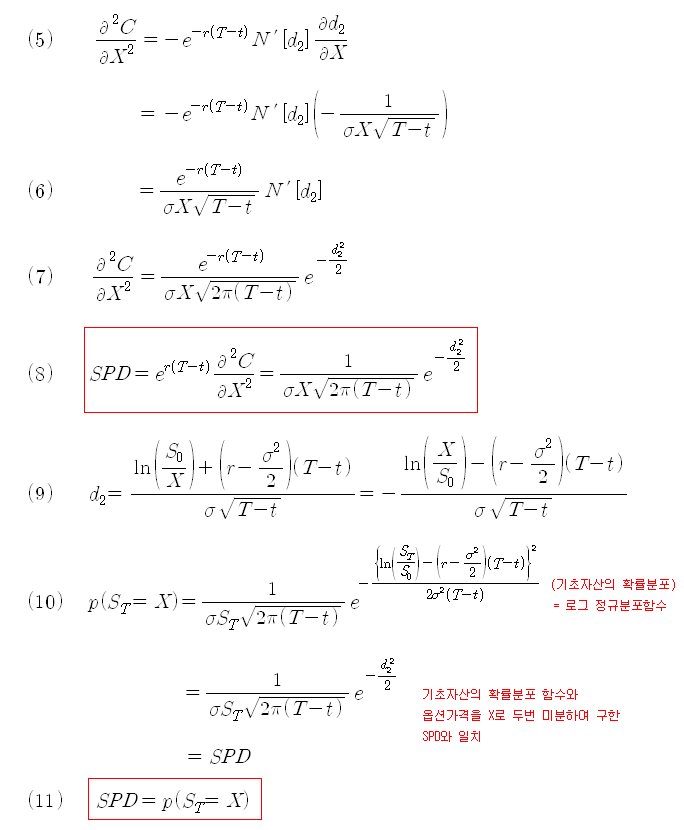News & Events
[금융수학] 18. 옵션의 행사가 민감도 및 SPD 공식유도 (Greeks : 행사가 민감도)
금융 수학 (18)
옵션의 행사가 민감도 및 SPD 공식유도 (Greeks : 행사가 민감도)
행사가 민감도는 행사가격 변화에 따른 옵션가격의 변화량으로, 옵션가격을 행사가격으로 편미분한 값이다. 행사가격이 1 단위 변할 때 옵션의 가격은 얼마큼 변하는가를 나타낸다. 행사가격이 증가할수록 옵션이 행사될 가능성이 낮아지므로 옵션가격은 하락하게 된다.
아래 그림은 엑셀에서, 콜옵션의 행사가격이 220.0 ~ 300.0 까지 변할 때, 행사가격별 콜옵션의 가격과 행사가 민감도를 계산한 것이다. 왼쪽 그림은 행사가격이 높아질수록 콜옵션의 가격이 낮아지는 모습을 보여주고 있다. 이것은 행사가격이 높아질수록 행사가능성이 작아지기 때문이다. 오른쪽 그림은 행사가격이 높아질수록 옵션의 가격이 하락하는 폭을 나타낸다. 행사가격이 상승할수록 옵션의 가격이 하락하므로 행사가 민감도는 음수 (-)의 값을 가진다. 행사가격이 낮을 때는 하락폭이 크고, 행사가격이 높아질수록 하락폭이 점점 감소하고 있는 모습이다. 또한, ATM 부근에서 하락폭이 급속히 감소한다.
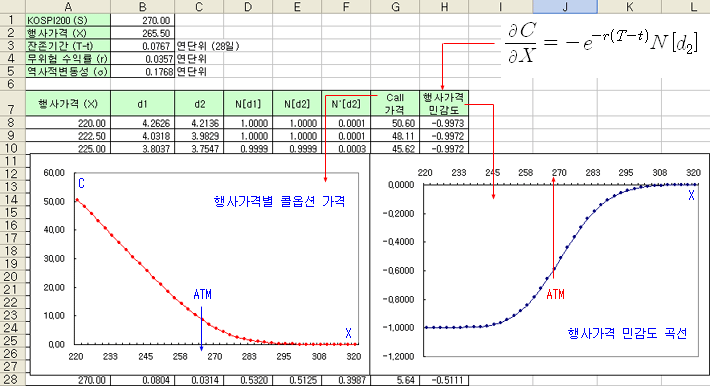
행사가 별 콜옵션의 가격은 주변 행사가의 옵션가격과 행사가 민감도만큼 차이가 나므로 일정한 궤도를 형성한다. 만약 특정 행사가의 옵션가격이 이 궤도를 벗어나면 차익거래가 발생하게 된다. 따라서 차익거래로 인해 옵션의 시장가도 이 궤도를 유지하게 된다.
행사가 민감도를 행사가격으로 한번 더 미분하면, 행사가 민감도의 기울기가 되고, 행사가격별 옵션의 가격하락 속도를 의미한다. 이 지표는 확률밀도함수가 (로그정규분포) 되고, 만기 시 기대 손익을 추정하는 함수로 사용될 수 있다 (아래 증명 참조). 이 함수를 State Price Density (SPD)라 한다. 옵션의 현재가는 만기 시 기대할 수 있는 기대손익을 현재시점으로 할인한 값과 일치해야 한다. 만기 시 기대손익을 구할 때는 (만기손익 * 확률함수)의 적분값으로 계산하는데, SPD를 확률함수로 적용할 수 있다는 의미이다.
아래 그림은 SPD를 계산하는 공식을 이용하여 SPD 분포를 그린 것이다. 현재 기초자산의 가격 부근에서 확률값이 최대가 되고, 양 옆으로 갈수록 로그정규분포의 형태로 확률이 감소한다. 이 함수는 만기 시 기대되는 기초자산의 분포로 해석될 수 있다.
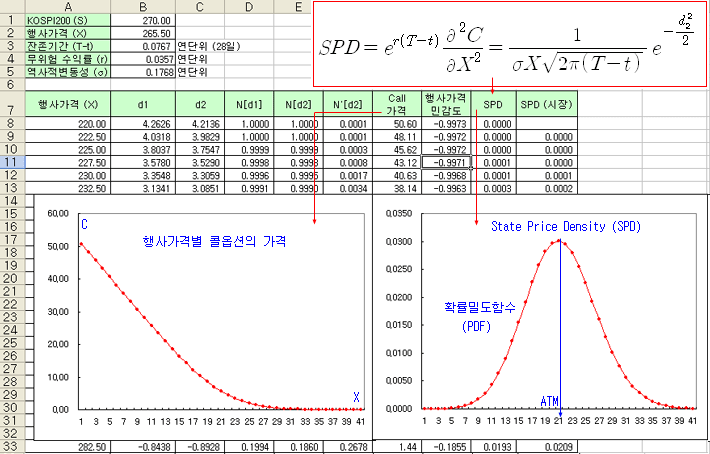
PD 분포를 이용하면 통계적차익거래를 고려해 볼 수 있다. 위 그림의 SPD는 블랙숄즈 모형으로 계산한 이론적 SPD 이고, 시장가로 추정한 SPD와 비교해 볼 수 있다. 만약 시장이 정상 상태라면 이론 SPD와 시장 SPD의 분포가 잘 일치할 것이나, 시장이 정상적인 상태가 아니라면 시장 SPD 분포가 왜곡되어 나타날 것이다. 시장 SPD 분포가 한 쪽으로 기울어지는 왜도 (Skewness) 현상이 나타날 수도 있고, 가운데가 뾰족하게 올라가거나 내려가는 첨도 (Kurtosis) 현상이 나타날 수도 있다. 만약 시장 SPD가 오른쪽으로 치우친 형태가 된다면, 시장의 심리는 오른쪽에 위치한 행사가격의 옵션이 행사될 가능성에 더 크다고 보는 것이다. 즉, 향후 기초자산의 주가가 상승할 것으로 기대하는 심리가 작용하는 것으로 해석한다. 이 성질을 이용하면 옵션의 왜도/첨도 차익거래 (Skewness and Kurtosis Strategy)를 고려해 볼 수 있다 (옵션의 통계적 차익거래 전략 참조).
엑셀에서 각 셀의 계산식은 아래와 같다.
* d1 : 셀(B8) = (LN(A8/$B$2)+($B$+($B$5^2)/2)*$B$3)/($B$5*SQRT($B$3))
d2 : 셀(C8) = B8-$B$5*SQRT($B$3)
N[d1] : 셀(D8) = NORMSDIST(B8)
N[d2] : 셀(E8) = NORMSDIST(C8)
N'[d2] : 셀(F8) = EXP(-(C8^2)/2)/SQRT(2*3.1416)
Call 가격 : 셀(G8) = A8*D8-$B$2*EXP(-$B$4*$B$3)*E8
행사가격 민감도 : 셀(H8) = -EXP(-$B$4*$B$3)*E8
SPD : 셀(I8) = F8/($B$5*A8*SQRT($B$3))
* 나머지 셀은 블랙숄즈 공식의 활용 – 엑셀 연습 참조
* 행사가 민감도의 유도과정 (블랙숄즈 옵션 공식의 미분방법 참조)
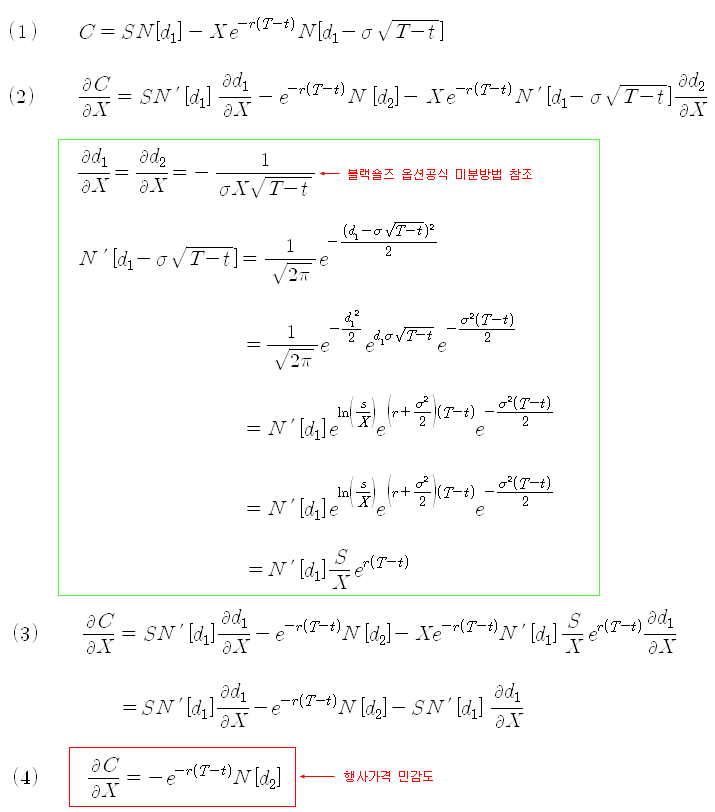
아래 식은 행사가격 민감도인 식 (4)를 X에 대해 한번 더 미분한 것이다. 미분한 결과는 식 (7)과 같이 되고, 여기에 exp{r(T-t)}를 곱해주어 SPD로 정의하면, 이 식이 바로 만기 시 기초자산의 가격이 X가 될 확률, p(ST = X), 과 정확히 일치한다. 즉 옵션 가격을 행사가격으로 2번 미분한 값을 만기 시 기초자산의 확률분포함수로 (로그 정규분포 함수임) 사용할 수 있다는 것을 의미한다.
