[금융수학] 20. 옵션과 민감도 간의 상호 관계

금융 수학 (20)

옵션과 민감도 간의 상호 관계

옵션과 민감도들의 관계를 이용하면, 민감도의 움직임에 따라 옵션의 가격을 표현할 수 있고, 합성 옵션으로 구성된 포트폴리오의 특성을 쉽게 파악해볼 수 있다. 그동안 살펴본 옵션의 민감도들을 정리해 보면 식 (1) ~ 식 (4)와 같다. (1)은 델타, (2)는 세타, (3)은 감마 그리고 (4)는 베가를 의미한다.

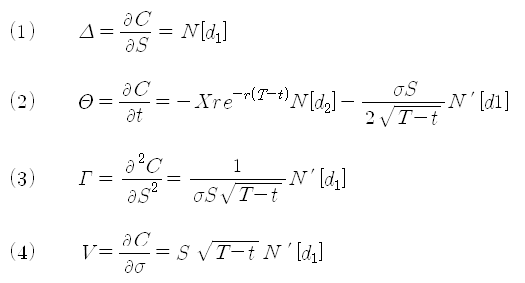
위의 식을 이용하여 다시 옵션의 가격을 표시해 보면 아래와 같이 된다. 식 (5)는 블랙숄즈의 콜옵션 가격이다. 이 식에 위의 값들을 대입하여 정리해 보면 식 (6)과 식 (7)을 얻을 수 있다. 각 민감도의 움직임으로 옵션의 가격을 표시한 것이다. 사실 식 (6)은 이미 블랙숄즈가 공식을 유도할 때 만든 편미분 방정식과 일치한다 (편미분 방정식 만들기 식 9 참조). 블랙과 숄즈는 이 편미분방정식을 풀어서 옵션 가격을 구한 것이고, 우리는 다시 옵션 가격을 미분하여 편미분방정식 꼴로 만들어 본 것이다.

이제 각 민감도에 대해 그 의미가 파악되었으므로 식 (6)이나 (7)을 사용하면 합성 옵션의 움직임을 파악하는데 도움이 많이 된다. 옵션만으로 구성된 포트폴리오를 만들면, 포트폴리오의 가치는 포트폴리오의 민감도에 따라 식 (8)로 표현할 수 있다. 또한, 각 민감도는 포트폴리오를 구성한 옵션의 선형조합으로 표현할 수 있다 (민감도의 가법성이 성립함).

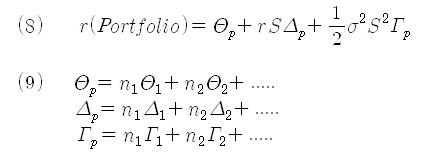
이제 식 (8)을 활용하는 방법에 대해 예를 통해 알아보자. 두 개의 옵션을 이용하여 식 (8)에서 포트폴리오의 델타가 0 이 되는 포지션을 만들어 보자. 델타가 0 이 되는 포지션을 델타-중립 포지션이라 한다 (Delta Neutral Position). 두 개의 옵션으로 델타 중립 포지션을 만들면, 옵션 상호간 델타 헤지 기능으로 서로의 델타를 상쇄하므로 포트폴리오의 델타는 0 이 되고, 기초자산 가격이 약간 변해도 포트폴리오의 프리미엄은 크게 변화가 없다.

델타 중립 포지션에서 합성 델타가 0 이므로, 식 (10), (11)과 같이 쓸 수 있고, 식 (11)은 델타 헤지 비율이 된다. 두 옵션의 매입/매도 비율을 식 (11)로 하면 포트폴리오의 델타를 0 으로 만들 수 있다. 물론, 이 상태에서 기초자산의 가격이 변하면 헤지 비율도 달라지기 때문에 합성 델타도 변하게 되지만, 기초자산의 가격이 미세하게 변한다면 합성 델타도 0 근처에서 크게 바뀌지 않는다는 것을 전제로 한다. 기초자산의 가격이 변해도 합성 델타가 0 이 되도록 유지하려면 동적 헤지 (Dynamic Hedge)를 해야 하지만, 이건 현실적으로 가능하지 않다. 실전에서는 기초자산이 크게 변화 했을 때 한 번씩 헤지 비율을 조정해 주기도 한다. 합성 감마식에 식 (11)을 대입하면 포트폴리오의 감마는 식 (12)와 같이 된다.

식 (8)에서 합성 델타에 0 을 대입 하면, 식 (13)과 (14)를 얻을 수 있다. 식 (13)은 기초자산 가격이 미세하게 변할 때 포트폴리오의 크기가 일정하다고 보면, 세타가 커질 때 감마도 반대 방향으로 커져야 하고, 반대로 세타가 작아지면 감마도 반대 방향으로 작아져야 한다는 것을 의미한다.

식 (14)도 마찬가지로 세타가 변할 때 베가도 반대 방향으로 같이 변해야 한다. 변화 속도를 알아보기 위해 식 (14)를 S로 다시 미분해 보면, 식 (15)와 같이 되고, 포트폴리오의 변화는 없으므로 식 (15)는 0 이 된다. 따라서 세타와 베가의 변화 속도도 일정하게 변화한다는 것을 알 수 있다 (변화 속도의 기울기는 서로 다르다).

실제 데이터를 이용하여 포트폴리오의 델타를 확인해 보자. 아래 테이블은 2012.4.27 현재 두 옵션의 실제 데이터이다 (S=263.11 임). 행사가격이 265.0인 콜옵션과 행사가격이 260.0인 풋옵션을 이용하여 델타 중립 포지션을 만들어 보자.

우선 두 옵션을 동시에 매입하거나, 동시에 매도하는 포지션을 생각해 본다. 이 포지션은 Straddle 매수나 매도 전략으로 알려져 있고, 실전에서는 양매수, 양매도 전략이라고도 부른다. 델타 중립이 되려면 두 옵션의 델타가 다르기 때문에 헤지 비율을 맞추어 주어야 한다. 식 (11)로 헤지 비율을 계산하면 풋옵션의 비율은 1.299이다. 이는 풋옵션의 델타가 (절대값) 콜옵션의 델타보다 작기 때문에 조금 더 비중을 두어야 한다는 의미가 된다. 그러면 +C+P 나, -C-P 포트폴리오의 합성 민감도도 위의 테이블과 같이 계산되고, 이것이 포트폴리오의 민감도가 된다. 포트폴리오의 델타가 0 임을 알 수 있다.

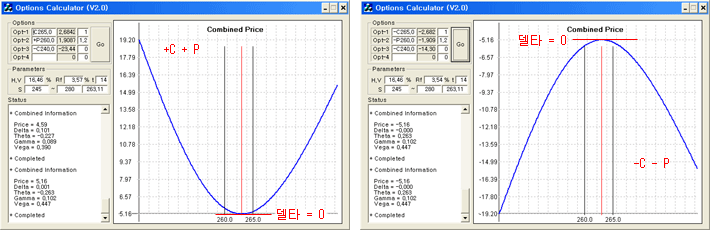
델타 중립 포지션의 손익 구조를 보면 위의 그림과 같다. 현재의 기초자산 가격 위치에서 합성 손익 그래프의 기울기가 0 이다. 즉, 기초자산이 미세하게 변화할 때 포트폴리오 가치의 변화가 거의 없게 된다.

위의 왼쪽 그림은 양매수의 경우로 시간가치인 세타를 지불하고, 베가나 감마의 이익을 기대하는 전략이다. 기초자산의 변동성이 커져서 위나 아래 방향으로 크게 움직이면 수익이 나는 모형이다. 그러나 시간가치는 크게 지불하여야 한다. 델타 중립 포지션에서 세타값은 최대가 되기 때문이다.

오른쪽 그림은 양매도의 경우로 베가나 감마의 위험을 감수하고, 시간가치인 세타를 취하려는 전략이다. 이는 기초자산의 변동성이 적을 것으로 예상될 때, 자연적으로 감소하는 시간가치인 세타를 취하려는 전략이다. 예상이 적중하면 이 위치에서 세타가 최대가 되므로 수익이 높아진다.

위의 두 전략 중 어느 것이 더 유리할까? 정상 시장이라면 당연히 똑같아야 한다. 즉, 두 전략의 기댓값은 동일해야 한다. E[ +Rc + hRp ] = E[ -Rc – hRp ] 이다 (h는 헤지 비율, Rc는 콜옵션의 수익률, Rp는 폿옵션의 수익률). 그러면 E[Rc] + hE[Rp] = -E[Rc] – hE[Rp] 이므로 E[Rc+hRp] = 0이 된다. 따라서 이 전략의 수익률 기댓값은 0 이 된다. 이것은 세타의 가치와 교환할 감마나 베가의 가치가 동일하다는 것을 의미한다.

델타 중립 포지션은 합성 수익 구조상 델타 = 0 이 될 수 있는 정점이 존재하는 경우에 모두 가능하다. 예를 들어 Strangle, Butterfly 등의 전략에서도 얼마든지 델타 중립 포지션을 구축할 수 있다.

이와 같이 식 (8)과 (9)를 이용하면, 감마-중립, 베가-중립, 세타-중립 등의 포지션에 대한 특성도 파악해 볼 수 있다.이상으로 옵션의 민감도의 관계를 통해 각 민감도의 움직임을 통해 합성 포지션의 특성을 파악하는 방법에 대해 살펴보았다.

[출처]20. 옵션과 민감도 간의 상호 관계|작성자아마퀀트