News & Events
[금융수학] 24. 변동성 지수 (Volatility Index : VIX)
- 2019년 1월 7일
- Posted by: 인사이트캠퍼스
- Category: 금융/AI/IT 기사

금융 수학 (24)
변동성 지수 (Volatility Index : VIX)
이전 포스트에서는 내재변동성 (Implied Volatility)이 행사가격별로 각각 다르게 측정되는 현상에 대해 살펴보았다. 이제는 여러 개로 측정되는 내재변동성 중에 어느 것을 적절한 변동성으로 인정해야할지를 고민해야 한다. 이 문제를 해결하기 위해서는 여러 개의 변동성을 적절히 조합하여 변동성을 대표할 수 있는 하나의 지수를 만들어야 한다. 이것이 바로 변동성 지수 (Volatility Index : VIX) 이다.
VIX는 1993년 Robert Whaley가 고안하여, CBOE (시카고 옵션 거래소)에서 채택된 것으로 향후 30일간의 변동성 지수로 환산하여 활용되고 있다. VIX는 미국의 S&P500 지수를 기준으로 발표되고 있으며, 우리나라에서는 KOSPI200 지수를 대상으로 V-KOSPI 지수로 발표되고 있다. 미국의 경우 2004년도에는 VIX를 활용한 선물거래가 개시되었으며, 2006년도에는 옵션거래도 시작되었다. 주가지수가 상승할 때는 VIX가 하락하다가, 주가지수가 하락할 때는 VIX가 상승하므로 VIX를 공포지수 (Fear Index)라고 부르기도 한다.
1987년 이후 변동성 미소 (Volatility Smile) 현상이 뚜렷해 졌고, 시장에서는 변동성을 대단히 중요한 의사결정의 요소로 보기 시작했다. 오히려 오랫동안 중요시되어 왔던 가격 (Price) 보다도 더 중요한 요소로 인식하게 되었다. 또한 가격에 대한 위험 헤지 수단은 많은 반면, 변동성 위험에 대한 적절한 헤지 수단이 없으므로, 변동성 자체를 하나의 상품으로 만들어서 거래하기 시작했다. 대표적인 것으로는, 아직 국내에는 도입되지 않았지만 (장외파생 거래는 있음), Variance Swap, Volatility Swap 같은 거래가 있다 (미국, 유럽, 일본, 홍콩 등.). 이러한 변동성 거래를 위해서는 현재의 변동성을 명확히 규정할 필요가 있으므로, VIX와 같은 변동성 지수가 탄생하게 되었다.
CBOE에서 발표한 변동성 지수의 산출 공식은 아래와 같다. 전 행사가격 중, OTM/ATM의 Put 가격과, Call 가격을 전부 조합하여 대표 내재변동성을 산출한 것이다. 각각의 의미는 아래와 같다.

T : 잔존만기를 나타내며 분 단위로 산출한다 (현재부터 만기까지의 분수)
델타K : 행사가격간의 차이 (우리나라는 2.5 임)
Ki : 행사가격
R : 무위험 수익률
Q(K) : 행사가격이 K인 OTM/ATM의 풋옵션 가격과 콜옵션 가격
F : Call 과 Put으로 산출된 합성선물가격. Call과 Put은 가격이 가장 유사한 것을 선택함.
K0 : F 보다 낮은 첫 번째 행사가격
각각의 의미를 정확히 이해하기 위해서는 실제 계산을 해 볼 필요가 있으므로, 다음 포스트에서 엑셀로 실제 계산을 해 보기로 한다. 여기서는 일단 VIX 산출 공식의 의미를 이해하도록 한다.
아래 그림은 행사가격별로 콜옵션의 가격과 풋옵션의 가격을 그린 그래프이다. 두 그래프가 만나는 지점의 C와 P를 이용하여 합성선물의 가격 (F)을 산출하면 그림에서 교차 지점의 위치가 F가 된다. VIX는 바로 아래 그림의 두 그래프가 교차하는 지점 아래의 면적으로 이해한다. C와 P가 교차되는 지점보다 위에 있는 C의 가격과 P의 가격 (ITM 부분)은 VIX 산출에서 제외한다.
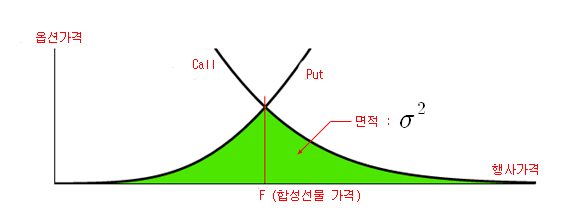
그림의 면적이 왜 변동성이 되는지를 이해하려면, 앞서 언급했던 변동성 거래 상품인 Variance Swap에 대해 이해할 필요가 있다. Variance Swap 거래란, 현재의 변동성과 미래 시점에서 실제 측정한 기초자산의 변동성을 서로 교환하는 거래이다. Variance Swap의 매수자는 현재의 내재변동성이 너무 낮다고 판단한 투자자이고, 향후 실제 변동성이 증가하면 수익을 내게 된다. 매도자는 이와 반대이다. Variance Swap은 옵션 등에 투자한 상태에서 향후 변동성이 증가할 위험을 헤지하는 수단으로 사용될 수도 있고, 실제 변동성에 투자할 목적으로 사용될 수도 있다.
위의 관계를 수식으로 표시하면 식 (1)과 같이 된다. Variance Swap의 매수자와 매도자는 미래 시점에 두 변동성의 차액으로 정산하게 된다. 이 상품도 마팅게일이 되려면 (즉, 차익거래가 발생하지 않으려면), 현재의 변동성이 미래의 실제변동성의 기댓값과 동일해야 하므로, 식 (2)와 같이 표현할 수 있다. 식 (3)에서 주가의 기하브라운운동의 모형에 변동성을 일정한 것으로 가정하지 않고, 확률변수로 놓고, 이 변동성의 기댓값을 계산하면 식 (4)와 같이 된다. 식 (3)에서 (4)로 전개되는 과정은 다소 복잡하므로 나중에 별도의 포스트에서 다루기로 한다.

위의 식 (4)가 바로 위에 있는 그림의 면적을 표현하고 있다. 따라서 그림의 면적이 현재의 변동성을 의미한다고 볼 수 있다. 여기서 식 (4)의 이산적 표현 (Discrete Version)을 VIX의 산출 공식으로 정의하였다. 위 공식의 두 번째 항은 VIX 계산값의 정확성을 높이기 위해 추가된 부분이다 (Correction term). C와 P가 그림의 교차되는 지점에서 정확히 만나지 않는 경우에는 위 그림의 초록색 면적 이외에 작은 삼각형의 면적이 추가되는데, 이 작은 삼각형의 면적을 빼 준 것이 바로 보정을 위한 부분이 된다. C와 P가 교차되는 지점에서 만나면 C-P=0 이 되므로 F = K0 가 되어 보정항은 0 이 된다 (자세한 것은 이후 포스트의 공식 유도 과정에서 살펴보도록 하겠다). 이렇게 계산된 VIX는 여러 옵션으로부터 추출한 현재의 내재변동성을 대표한 대표 내재변동성이 된다.
실제로 발표되는 VIX 값은 이 계산값을 보정하여 향후 30일 간의 변동성으로 표시한다. 향후 30일 간의 변동성으로 환산하기 위해서는 근월물 옵션의 가격으로부터 산출한 변동성과, 차월물 옵션으로부터 산출한 변동성을 기간의 가중평균으로 계산한다. 이 관계식은 아래와 같으며, 향후 30일 간의 변동성을 연간단위로 표시한 식이 된다.
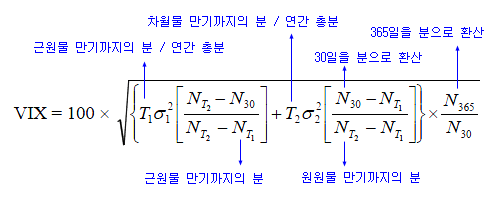
VIX를 실제 트레이딩에 이용해 보려면, 발표되는 30일 간의 VIX를 이용할 경우도 있지만, 위에서 계산한 대표 내재변동성을 그대로 이용할 수도 있다. 알고리즘 트레이딩에서 매매신호 검출 등에 VIX를 실시간으로 이용하려면 맨 위에 식으로 직접 계산하여 사용할 수도 있다.
Reference : http://www.cboe.com/micro/vix/vixwhite.pdf

