[금융수학] 26. 로그 계약 (The Log Contract)

금융 수학 (26)

로그 계약 (The Log Contract)

이번 시간에는 변동성 (Volatility)과 관련된 아주 흥미로운 식을 도출해 본다. 주가의 수익률에는 일반적인 수익률과 로그 수익률이 있다. 주식을 매수하면 일반적인 수익률에 따라 손익이 결정된다. 그러나 금융공학에서는 많은 이점 때문에 로그 수익률을 사용하며, 일반적인 수익률과는 약간의 차이가 발생한다.

만약, 로그 주가가 거래되는 시장이 있다고 가정해 보자. 그리고 투자자가 일반 주가를 매수하여 일반 수익률을 매수하고, 로그 주가를 매도하여 로그 수익률을 매도한 상황을 가정해 보자. 그러면 손익은 Pay off = 일반 수익률 – 로그 수익률을 따를 것이다.

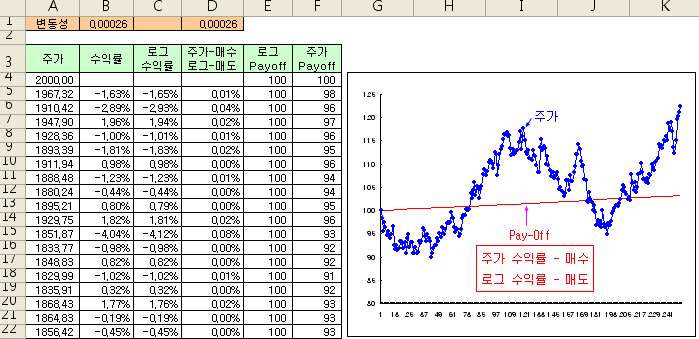
이 상황을 가정하여 위의 그림을 그려 보았다. 열(A)에 1년간의 주가 변화가 있을 때, 열(B)와 열(C)에 일반 수익률과 로그 수익률을 계산하고, 일반 수익률을 100원 어치 매수하고, 로그 수익률을 100원 어치 매도한 상황을 가정해 보자. 이때 손익의 변화는 열(E)에 계산되어 있다.

* 셀(B5) = (A5 – A4)/A4,    셀(C5) = ln(A5/A4),    셀(D5) = B5 – C5

셀(E5) = E4 * (1 + D5),   셀(F5) = F4 * (1 + B5)

일반적인 경우와 같이 주가를 100원 어치 매수했을 때 손익의 변화는, 열(F), 주가의 변화와 같고, 그림에서 파란색 그래프와 같이 움직인다. 그러나 주가 수익률을 매수하고, 로그 수익률을 매도한 손익은, 열(E), 빨간색 그래프와 같이 움직인다. 여기서 특이한 사항은 빨간색 그래프는 항상 직선으로 나타난다는 점이다. 그럼 빨간색 그래프가 의미하는 것은 무엇이고, 왜 항상 직선으로 나타나는가? 이것이 변동성과 관련하여 아주 흥미로운 사실이고, 바로 변동성을 매수하거나 매도하는 효과가 된다.

이 원리로 변동성을 직접 거래하는 아이디어로, 1994년 영국의 Anthony Neuberger 교수는 “The Log Contract” 이라는 논문을 발표하였다. 비록 이 거래가 거래소에서 채택되지는 않았지만, 변동성과 관련된 파생상품 계산에 이 아이디어가 아주 많이 쓰이고 있다.

이제 두 수익률의 차이와 변동성과는 어떤 관계가 있는지 수식으로 살펴보자. 식(1)은 브라운운동의 주가 모형이고, Drift인 u는 일정하고, 변동성인 시그마는 시간(t)과 주가(S)에 따라 변하는 것으로 설정 한다. 블랙-숄즈에서는 변동성을 일정하게 놓고 사용하였으나, 여기서는 변동성이 계속 달라지는 실제적인 상황으로 설정한다.

식(2)는 변동성이 일정하지 않은 경우의 식(1) 방정식의 해의 모습이다. 식(2)의 양변에 로그를 씌우면 식(3)이 되고, 양변을 미분하면 식(4)와 식(5)가 된다.

식(5)의 dW 항을 식(1)을 이용하여 대체하면, 식(6)과 식(7)을 얻을 수 있고, 식(7)의 양변을 다시 적분하면 식 (8)이 된다. 식(8)에서 우변의 두 번째 적분항은 분산 (변동성)의 총합을 의미하므로, 분산의 평균을 계산하려면, 기간수 (T)로 나누어 주면 된다. 즉, 분산의 평균은 식(9)로 표시할 수 있다. 예를 들어 일일 변동성을 252일간 합한 후 (0 ~ T), 다시 252 (T)로 나누어 주면 식(9)는 일일 평균 변동성이 되고, 이것이 실제 변동성이 된다. (식-7 부터는 표기를 간단히 하기위해 S에 첨자를 생략하였다.)

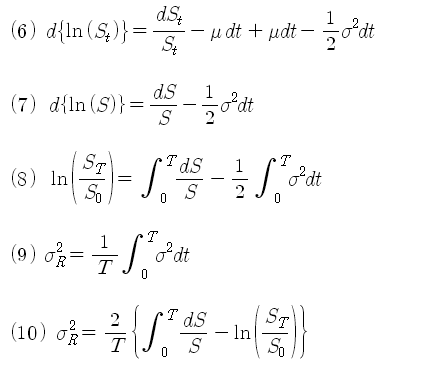
식(8)에 식(9)를 대입하고, 실제 변동성에 대해 정리하면 식(10)을 얻을 수 있다. 식 (10)을 이산모형으로 근사시켜 보면 식(11)과 같이 쓸 수 있고, 식(12)는 h-시점의 Pay Off가 된다. 식(11)의 우변이 바로 일반 수익률과 로그 수익률의 차이이고, 이 차이를 매일매일 일일정산 (Marking-to-Market)하고 있는 모습이다. 그런데 이 결과가 바로 좌변의 실제 변동성과 일치한다. 즉, 일반 수익률을 매수하고, 로그 수익률을 매도한 것은 바로 변동성을 매수한 것과 동일하다. 이러한 개념을 통해, 추상적인 변동성을 직접 거래가 가능한 하나의 Asset으로 취급할 수 있으며, Pricing 까지도 가능하게 되는 것이다.

식(11)을 확인하기 위해 다시 맨 위의 엑셀 파일로 돌아가 보자. 셀(B1)은 주가 수익률의 분산으로 실제 변동성을 의미한다. 셀(D1)은 식(11)의 우변을 계산한 결과이다. 두 셀의 값이 잘 일치한다. 식(11)의 우변이 실제 변동성을 의미한다는 것을 확인해 본 것이다.

* 셀(B1) = VAR(B5:B254)

셀(D1) = 2 * SUM(D5:D254) / 250

맨 위의 그래프를 다시 해석해 보자. 빨간색 그래프가 직선으로 나타나는 것은 바로 변동성을 매수한 경우 손익 구조가 직선이 된다는 것을 의미한다. 또한, 변동성이 증가하면 직선의 기울기가 커지고, 변동성이 작아지면 기울기가 작아진다. 즉, 위의 포트폴리오는 변동성을 매수한 것과 동일하므로, 변동성이 커질수록 수익이 증가한다는 것을 의미한다.

이번 시간에는 로그 수익률과 변동성에 대한 흥미로운 내용을 다루어 보았다. 이 내용을 다룬 이유는 이전 포스트의 VIX 공식 산출 과정을 자세히 다루기 위해 필요한 사전 지식으로, 다음 포스트에서 다룰 Variance Swap에서 식(12)를 사용하기 때문이다.

[출처]26. 로그 계약 (The Log Contract)|작성자아마퀀트