[금융수학] 27. VKOSPI 계산의 질문에 대한 답변

금융 수학 (27)

VKOSPI 계산의 질문에 대한 답변

어는 분이 실시간 VKOSPI 계산 과정에서 발견된 특이사항에 대한 질문을 주셨습니다. 질문 내용이 너무 중요한 것 같아 포스트를 통해 답변을 공유합니다.

질문내용 :

1. VKOSPI 계산 공식에서 K0 를 선택하는 데 문제가 발생함.

2. (C – P) 의 절대값이 최소가 되는 K 를 선정하여 F를 계산하였음.

3. 해당 K 에서 C > P 인 경우와, C < P 인 경우에 K0 의 선택에 따라 VKOSPI의 결과가 크게 달라짐.

4. 이 블로그의 내용대로 F 보다 작고 F 에 가장 인접한 K0 를 선택하면 C > P인 경우에는 별 문제가 없지만,

갑자기 C < P 가 되면 VKOSPI 계산값이 크게 달라지는 현상이 발생함.

답변 :

이 블로그에서는 CBOE의 자료를 참조하여 VKOSPI를 계산하였다. 위의 문제를 해결하기위해 KRX에서 배포한 VKOSPI 자료를 찾아보았더니 아래와 같이 설명되어 있었다.

* KRX  자료 : K0 ~ 선도지수 (F)와 같거나 높은 행사가격 중 당해 선도지수와 가장 가까운 행사가격

* CBOE 자료 : K0 ~ First strike below the forward index level, F

두 자료를 비교해 보면 KRX 자료에는 “높은 행사가격 중” 으로 되어 있고, CBOE 자료에는 “below” 라고 되어 있다. 어떤 게 맞을까? (애매하네요.) 정확한 해답을 찾기 위해서는 VIX 공식을 세부적으로 분석해 볼 필요가 있다. 해답은 바로 보정을 위해 추가된 부분에 있었다.

정답 : C > P 인 경우에는 F 바로 아래에 있는 K를 선택함.

       C < P 인 경우에는 F 바로 위에 있는 K를 선택함.

설명 :

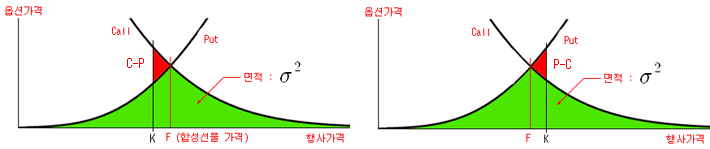
VKOSPI (VIX)의 계산 결과는 위 그림의 초록색 부분의 면적이다 (공식의 각 항에서 K 제곱으로 나누어 준 부분이 있으므로, 정확히 면적을 의미하는 것은 아니지만, 면적으로 이해하기로 한다). 그러나 C와 P가 두 곡선이 교차하는 지점에 정확하게 위치하지 않으면, 위 그림과 같이 빨간색 면적이 추가되므로 이 부분을 빼 주어야 한다 (이산 모형의 경우). 각 경우의 빨간색 면적은 삼각형으로 간주하여 아래와 같이 근사적으로 구할 수 있다. 두 경우의 결과는 동일하다. (C-P)는 풋-콜페리티를 이용하면 (F-K)exp(-rT)로 쓸 수 있다.

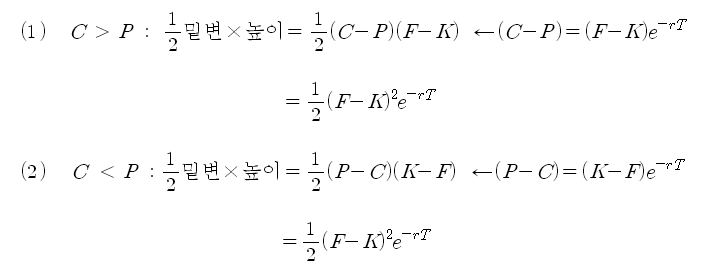
VIX의 원래 공식에서 위의 삼각형 면적을 빼 주면 아래와 같이 된다.

위의 결과와 같이 VIX 공식에서 두 번째 항인 보정항 (Correction Term)은 바로 위의 빨간색 부분의 면적을 빼준 것을 의미한다. 만약 C와 P가 두 곡선의 교차점에 정확히 위치하면 C – P = 0 이 되고, F = K 가 되므로, 보정항은 0 이 된다. 이제 보정항의 의미를 정확히 알았으므로 K0 를 선택하는 기준이 명확해 졌다.

* K0 선택 기준 : C > P 인 경우에는 F 바로 아래에 있는 K를 선택함.

C < P 인 경우에는 F 바로 위에 있는 K를 선택함.

그런데, 이렇게 결론을 내리면 한 가지 의문이 또 생긴다. 위의 기준대로라면 그냥 C – P 의 절대값이 최소인 K 를 선택하는 것과 동일해 진다. C가 큰지 P가 큰지를 따질 필요가 없어진다. 이에 대한 해답을 얻기 위해 아래의 그림을 생각해 본다.

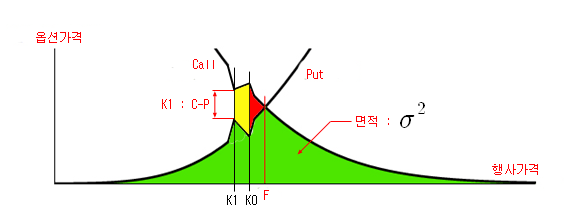
맨 위의 그림은 C와 P의 가격이 정상적인 경우이며, 정상적인 경우에는 C – P 의 절대값이 최소인 K를 K0로 선택하면 될 것이다. 그러나 C나 P의 시장 가격이 순간 왜곡되어 그림과 같은 현상이 발생한다면 상황은 달라질 것이다 (그림은 설명을 위해 왜곡을 심하게 그림). C – P 의 절대값이 가장 작은 행사가격은 K1 이 될 것이고, K1 을 기준으로 F를 계산하게 될 것이다. 그러면, (처음 ~ K1) 까지는 Put의 가격으로 계산하고, (K1 ~ 끝) 까지는 Call의 가격으로 계산할 것이다. 그럼 총 면적은 초록색 + 빨간색 + 노란색이 된다. 정확한 보정을 위해서는 빨간색과 노란색의 면적을 모두 빼 주어야 한다. 그런데 이 모든 경우를 다 고려하여 수식을 만들기는 쉽지 않을 것 같다.

위 그림에서 어떤 형태인지는 잘 모르겠지만 일정 부분의 면적을 더 빼 주어야하는 것은 확실한 것 같고, C와 P의 가격이 정상적인 경우보다는 조금 더 많은 면적을 빼 주어야 할 것 같다. 그런데 K0 > K1 이므로, 보정항에 K1을 넣는 것 보다 K0를 넣는 것이 조금 더 많이 빠진다. 그러므로 K1을 선택하는 것 보다는 K0를 선택하는 것이 오차가 줄어들 것이다. 아마도 이런 이유로 문서에서는 “F에 인접한” 행사가격으로 정의한 것으로 보인다.

이런 논리로 생각해 보면 그런대로 잘 이해가 된다. 최종 결론으로, 위에서 내린 K0의 선택 기준은 타당한 것 같고, 추가적으로는 그림과 같이 가격이 왜곡된 경우에는 미세하게나마 VKOSPI 값이 크게 측정될 수 있다는 사실을 염두에 두면 될 것 같다 (의사 결정시 참고사항).

좋은 질문을 주신 분께 감사드립니다.

[출처]27. VKOSPI 계산의 질문에 대한 답변|작성자아마퀀트