[금융수학] 28. 일반화된 Payoff 함수

금융 수학 (28)

일반화된 Payoff 함수

지난 시간에는 로그 계약 (The Log Contract)의 개념을 통해 변동성을 거래할 수 있다는 개념과, 그 손익관계 (Pay Off)에 대해 살펴보았었다. 이번 시간에는 옵션으로 로그 계약을 복제할 수 있도록 연결 고리를 만들어 주는 Pay Off 함수에 대해 알아본다.

아래 식은 일반화된 (Generalized) Pay Off의 관계식이다. 좌변을 임의의 포트폴리오에 대한 Pay Off라 할 때, 우변과 같이 분해하여 (Decomposition) 표현할 수 있다. 이 식은 일반적인 함수의 Taylor 급수로 이해할 수 있다. 이 식이 바로 옵션으로 로그 계약을 복제할 수 있는 수단을 제공해 준다.

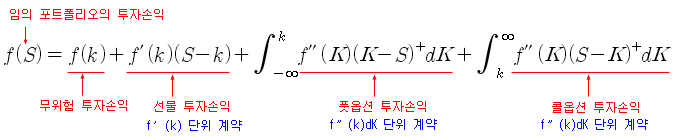
위의 식에서 (K – S)+ 의 의미는 K > S 이면 (K – S)가 되고, K < S 이면 0 이 되는 표현이다. S 는 기초자산, k 는 임의의 가격, 그리고 K 는 행사가격이라고 생각해 본다. 그러면 좌변의 f(S)는 기초자산 S에 대한 함수로 S의 변화에 따라 손익이 결정되는 함수로 생각할 수 있다. 우변의 첫 번째 항은 임의의 가격에 대한 손익으로 채권과 같은 무위험투자 손익으로 생각할 수 있고, 두 번째 항은 인수도 가격 (Delivery Price)이 k인 선물을 f'(k) 단위만큼 계약한 경우의 손익으로 생각할 수 있다. 세 번째 항은 행사가격이 K인 풋옵션을 f”(K)dK 단위만큼 계약한 경우의 손익이고, 네 번째 항은 행사가격이 K인 콜옵션을 f”(K)dK 만큼 계약한 경우의 손익으로 생각할 수 있다. 즉, 이 식은 채권 + 선물 + 옵션을 이용하면 어떠한 포트폴리오도 복제할 수 있음을 시사하고 있다. 이것은 대단히 중요한 의미를 가지는 식으로, 가격결정 이론에 널리 이용되고 있다. VIX (VKOSPI) 공식도 이 식을 바탕으로 로그 계약을 복제하여 만들어 낼 수 있다.

다음 시간에는 위의 식과 이전 포스트의 로그 계약의 Pay Off 식을 이용하여 VIX (VKOSPI) 공식을 완성해 보기로 하고, 여기서는 위의 식이 나온 과정만 간단히 살펴보도록 하겠다.

위의 식은 단순히 Taylor 급수를 이용하여 만들어 볼 수 있다. 아래 식(1)은 일반적으로 성립하는 식이다. 여기에 부분적분을 이용한 식 (3)을 대입해 보면 식 (4)를 얻을 수 있다.

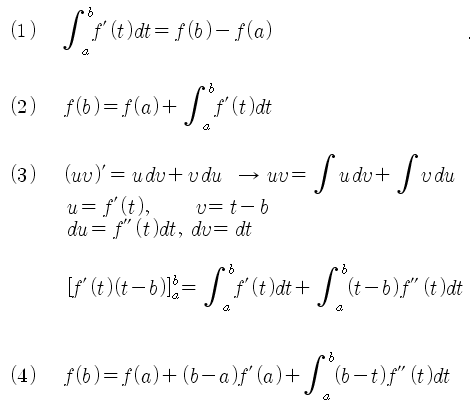
식 (4)는 Taylor 급수식의 일반적인 표현이다. 여기서 b 에는 S를 대입하고, a 에는 k, 그리고 t 에는 K를 대입하면 식 (5)와 같이 표현할 수 있다. 식 (5)의 적분항을 두 부분으로 나누어 쓰면 식 (6)이 된다. 식 (6)은 S > K 인 경우와 S < K 인 경우로 나누어 표시한 것이다. S > K 인 경우는 (S – K)+ = (S – K), (K – S)+ = 0 이고, S < K 인 경우는 (S – K)+ = 0, (K – S)+ = (K – S) 가 되어 식 (5)와 같아진다. S가 기초자산의 가격으로 생각하면 0보다 크고 무한히 커질 수 있으므로 식(7)과 같이 표현할 수 있고, S 가 (-)의 값을 가질수 있는 일반 변수라면 식 (8)로 표현할 수 있다.

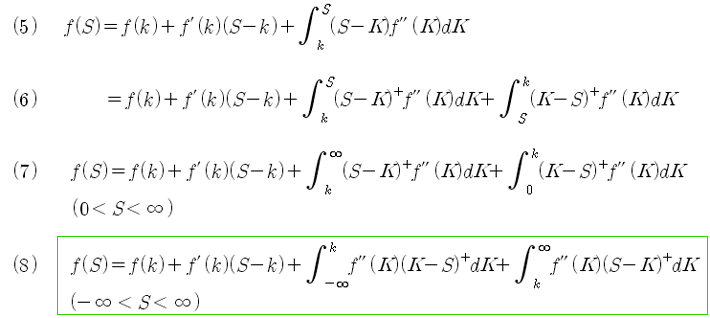
식 (8)이 바로 일반화된 Pay Off 함수이다.

[출처]28. 일반화된 Payoff 함수|작성자아마퀀트