News & Events
[금융수학] 3. 블랙 숄즈 옵션공식 유도 (2) – 편미분방정식 풀기 (PDE 1/3)
금융 수학 (3)
블랙-숄즈 옵션공식 유도(2) -편미분방정식 풀기 (PDE 1/3)
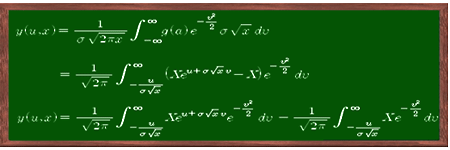
이전 포스트에서 만든 블랙 숄즈 편미분 방정식은 아래의 1) 식과 같다. 이제부터 3회에 걸쳐 이 편미분 방정식을 고전적 방법인 PDE (Partial Differential Equation) 방식으로 풀어서 방정식의 해인 f(t, S)를 구해 본다. 이 해가 바로 콜 옵션의 가격을 결정하는 그 유명한 블랙 숄즈의 옵션가격결정 공식이 된다. 여기서 부터는 금융 지식과는 상관없이 단순히 수학적으로 풀어나가기만 하면 된다.
식 1)에 대한 경계 조건은 식 2)와 같이 된다. 옵션의 만기(T) 가치는, 만기 시의 주가(S)와 행사가격(X)에 따라 결정된다. 만기 시 주가(S)가 행사가격(X) 보다 크면 이 옵션의 행사 가치는 (ST – X)가 되고, S가 X보다 작으면 이 옵션은 행사되지 못하므로 가치가 소멸된다.
편미분 방정식의 풀이 과정
식 1)과 식 2)를 간단히 하기 위해 아래와 같이 변수를 치환한다. x = T – t 는 잔존 기간을 의미하고, 만기 시점에서는 T = t 이므로 T – t = 0 이 된다. 그러면 식 2)의 경계 조건은 식 4)와 같이 된다.
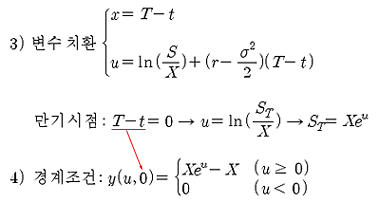
여기서 식 1)의 해의 모양을 아래와 같이 표현해 보자.
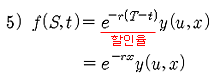
위 식은 잔존 기간이 x일 남은 옵션의 가치를 y(u, x)라 할 때, 이 옵션의 현재가치 f(S, t)는 y(u, x)를 현재 가치로 표현한 식이므로, f(S, t)는 이와 같은 형태가 될 것이라는 가정은 타당하다.
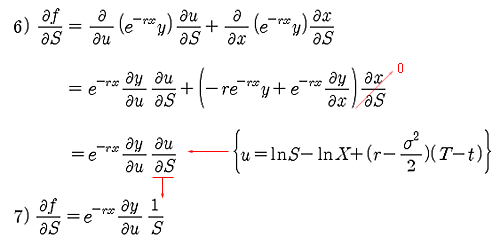
식 5)로 표현한 해 f(S,t)를 S에 대해 편미분을 해 보면, 식 6)과 같이 된다. 식 6)의 마지막 식에서는 식 3)에서 치환한 변수인 u를 S에 대해 편미분 하면 1/S 가 되어 식 7)을 얻을 수 있다. 동일한 방식으로, f(S, t)를 t에 대해 편미분을 하고, S에 대해 2번 편미분 하면 아래와 같이 된다.
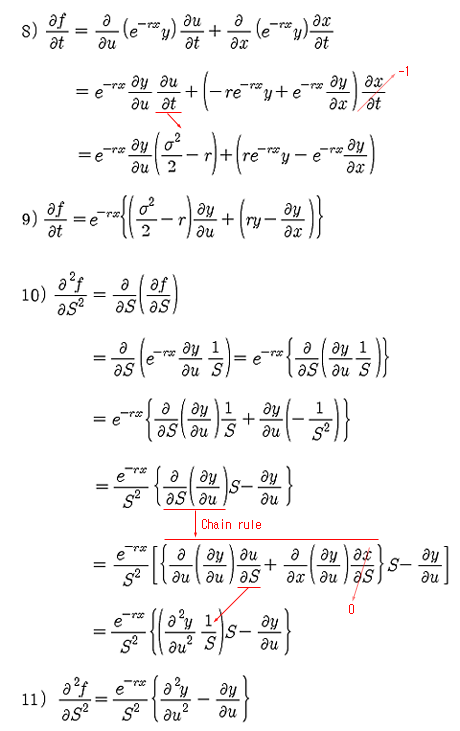
식 10)의 5 번째 식은 다변수 함수의 Chain rule을 적용시킨 것이다. f가 S와 t의 함수이고, S와 t는 각각 u와 x의 함수이므로 4 번째 식에 Chain rule을 적용시켜 5 번째 식을 만들 수 있다. 여기 까지가 식 1)의 우변의 3개 항을 각각 계산한 것이다. 이 3개 항은 각각 식 7), 9), 11) 과 같고, 이 3 식을 다시 식 1)에 대입하면 아래와 같다.
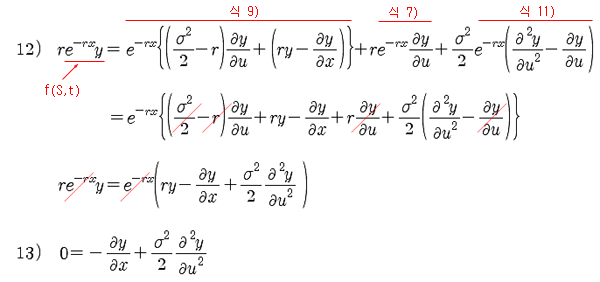
식 13)을 최종 정리해 보면 아래와 같다.
여기 까지가 변수 치환을 통해 1)식을 간단히 만든 과정이다. (놀랍게도) 식 14)는 물리학에서 다루는 열이 전달되는 열 확산 방정식이다. 어느 지점에 열원이 있고 시간에 따라 열이 전달되는 과정을 표현한 방정식이다. y를 일정 시간 후의 어느 지점의 온도라고 하고, 시그마^2 은 열이 흐르는 물질의 특성을 나타내는 상수라 하고, x를 시간 (t)이라 하고, u를 열이 흐르는 공간 축이라고 보면 완전히 동일한 식이 된다. 즉, 이 방정식은 이미 물리학자들이 해 (y의 함수식)를 구해놓은 상태이므로, 옵션의 가격을 결정하는 공식도 구할 수 있다는 뜻이 된다.
다음 포스트에서는 이 방정식의 해인 y의 함수를 구해 보도록 한다.
참고자료 : 블랙 숄즈의 편미분 방정식 (1999. Ishimura Sadao & Sonolsu)
수리물리학 (Boas/강주상)
