News & Events
[금융수학] 4. 블랙 숄즈 옵션공식 유도 (3)-편미분 방정식 풀기 (PDE 2/3)
금융 수학 (4)
블랙 숄즈 옵션공식 유도 (3)-편미분 방정식 풀기 (PDE 2/3)
이전 포스트에서 변수 치환을 통해 블랙 숄즈 편미분 방정식을 간단히 만들어서 아래의 식 1)과 같이 표현 하였다. 이번 시간에는 식 1)의 편미분 방정식을 풀어서 그 해인 y(u, x)를 구해 보도록 하겠다. y(u, x)만 구하면 최종 해인 f(S, t)를 구할 수 있다.
이 방정식은 이전 포스트에서도 언급하였지만 물리학의 열 확산 방정식이다. 이 방정식을 풀기 위해 수리물리학의 열 확산 방정식의 풀이를 참조하였다. y(u, x)를 온도 함수라 할 때 이 함수를 공간 부분 F(u)과 시간 부분 T(x)으로 분리하여 식 2)와 같이 쓸 수 있다. F(u)는 열이 전달되는 공간에 대한 함수이고, T(x)는 시간에 대한 함수이다. 즉, T(x) 시간 후에 F(u) 지점의 온도는 얼마나 되는가 하는 문제가 되고, 우리의 문제로는 잔존기간이 T(x) 남은 옵션 F(u)의 가격은 얼마가 되는가로 이해하면 된다. (여기서 T는 만기를 의미하는 것이 아니라 시간의 함수를 의미한다).
식 2)을 각각 u와 x에 대해 편미분하고, 그 결과를 식 1)에 다시 대입하면 식 3)을 얻을 수 있다. 여기서 k는 분리 상수 (Separation constant)이고 음수의 형태를 취한 이유는 조금 뒤에 설명하겠다. 분리 상수 k를 이용하면 식 3)을 아래와 같이 식 4)와 식 6) 으로 각각 나누어 쓸 수 있다.
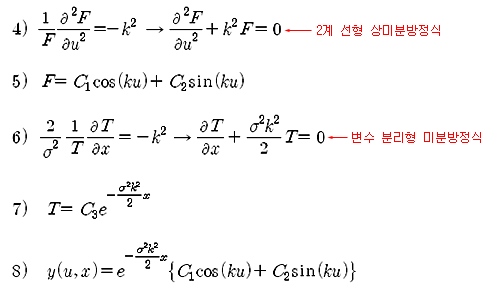
식 4)는 2계 선형 상미분 방정식으로 해는 식 5)와 같이 되고, 식 6)은 변수 분리형 미분 방정식 이므로 해는 식 7)과 같이 된다. 만약 분리 상수를 양수로 놓았다면 식 7)에서 잔존 기간 x가 증가할수록 T는 무한히 증가하여 원하는 결과를 얻을 수 없다. 열 확산 방정식의 경우는 시간이 지남에 따라 온도가 무한히 상승하는 식을 피하고자 분리 상수는 음수로 놓았다. 이런 이유로 식 3)에서 분리 상수를 음수로 놓은 것이다. 식 5)와 7)의 F 와 T 를 식 2)에 대입하면 y(u,x)의 표현식인 식 8)을 얻을 수 있다. 여기서 구한 y(u,x) 보다 더 일반적인 해는 식 9)와 같이 식 8)의 선형 조합으로 표현된다 (중합의 원리).
따라서 이 방정식의 일반해는 k가 연속인 경우 식 9)와 같이 쓸 수 있고, 적분상수 C1, C2를 구하기 위해 식 10)과 같이 경계 조건을 이용한다. 여기서 C1, C2는 Fourier 적분 전개 계수가 되므로 식 11)과 같이 쓸 수 있다 (공업수학 Fourier 급수 참조). C1, C2를 식 10)에 대입하면, 일반해는 식 12)와 같이 쓸 수 있다
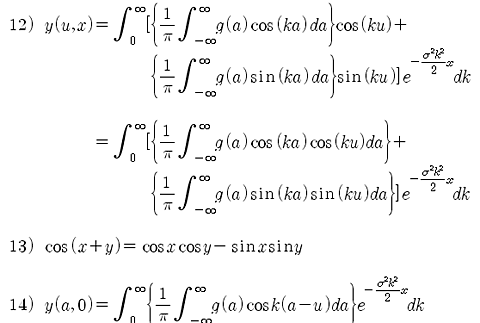
식 12)를 정리하고, 식 13)의 성질을 이용하면 식 14)가 된다. 여기서 적분 순서를 변경하면 식 15)가 된다.
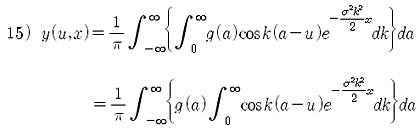
여기서 참고로 일반 미적분학을 참조하여 식 16)의 성질을 이용할 수 있다. 식 16)을 식 15)에 대입할 수 있는 형태로 변환하기위해 식 16)부터 식 20) 까지의 과정을 거친다.
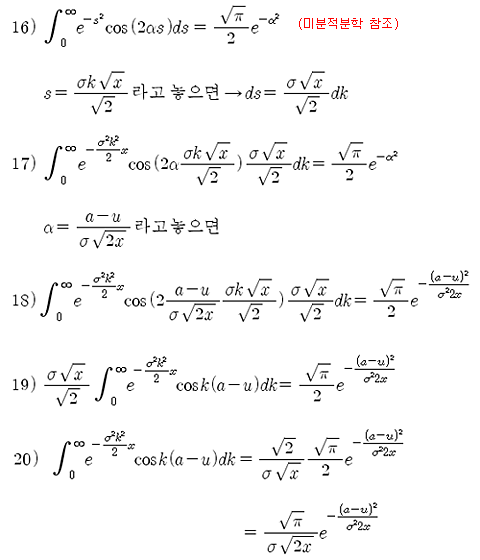
식 20)의 결과를 식 15)에 대입하면 최종적으로 식 22)를 얻을 수 있다. 식 22)는 우리가 얻고자 하는 y(u, x) 함수의 형태를 취하고 있다.
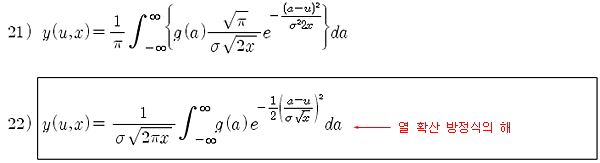
여기서 g(a) 는 만기 시점의 y(u, 0) 이므로, 거의 해에 가까운 모습을 하고 있다. 이제 조금만 더 가면 우리가 원하는 해를 얻을 수 있을 것 같다. 다음 포스트에서 블랙 숄즈 옵션 공식을 완성해 보기로 한다.
참고자료 : 블랙 숄즈의 편미분 방정식 (1999. Ishimura Sadao & Sonolsu)
수리물리학 (Boas)
공업수학 (Kreyszig)
