[금융수학] 6. 블랙 숄즈 공식의 활용 – 엑셀 연습

금융 수학 (6)

블랙 숄즈 공식의 활용 – 엑셀 연습

이전 4 편의 포스트를 통해 유도한 블랙 숄즈의 옵션가격결정 공식을 활용하는 방법에 대해 알아보자. 엑셀을 통해 금일 (2012년 3월 20일) 콜옵션의 이론가를 직접 계산해 본다. 아래 그림의 좌측 화면은 HTS에서 보여주는 행사가격 280에 대한 콜옵션의 기본 정보이다. 기초자산인 KOSPI200의 금일 현재가는 269.68이고, 만기까지의 잔존 기간은 18 거래일이며, 역사적변동성 (HV)은 22.94% 이다. 이 정보를 이용하여 잔존기간이 18 거래일 남은 콜옵션의 이론가격을 직접 계산해 보자.

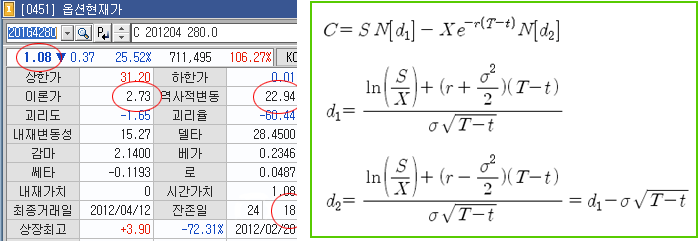
역사적 변동성 (HV 혹은 시그마)은 KOSPI200의 일일 변동성 (일일 수익률의 표준편차)을 연간 변동성으로 환산한 값이다. 역사적 변동성의 계산은 일정 기간 동안 (HTS에서는 보통 90일 간으로 함)의 KOSPI200 수익률을 계산한 다음, 수익률의 표준편차를 구해서 sqrt(252)를 곱해주면 된다. 252는 연간 주식 거래일 수를 의미하고, sqrt (루트)는 연간 변동성으로 환산하기위해 곱해 준다 (이 부분은 향후 Random Walk 부분에서 자세히 언급하도록 하겠다).

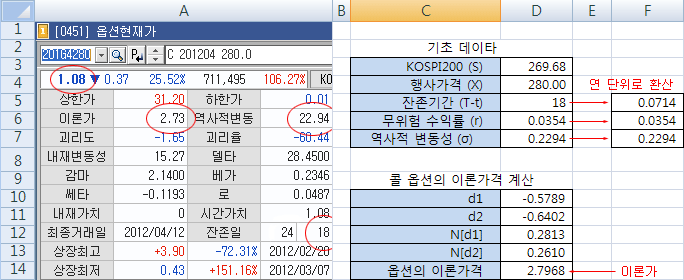
위 그림의 오른쪽 화면은 엑셀에서 이론가를 직접 계산한 결과이다. 기초 데이터 중 잔존기간, 무위험 수익률, 역사적 변동성은 연간 단위로 환산하여 공식에 대입한다. 1년 중 주식 거래일 수는 보통 252일로 하기 때문에, 비율에 맞추어 연간으로 환산한다. 무위험 수익률은 CD 금리 (3.54%)를 적용하였다. 이론가격 계산은 아래와 같이 블랙 숄즈의 옵션 공식에 그대로 대입하면 된다.

* 잔존기간 (연 단위), 셀(F5) = 셀(D5) / 252

무위험 수익률, 셀(F6) = 0.0354 (이미 연간 단위임)

역사적 변동성, 셀(F7) = 0.2294 (이미 연간 단위임)

* 콜옵션의 이론가격 계산

d1 계산 : 셀(D10) = (LN(D3/D4)+(F6+(F7^2)/2)*F5)/(F7*SQRT(F5))

d2 계산 : 셀(D11) = D10-F7*SQRT(F5)

N[d1] 계산 : 셀(D12) = NORMSDIST(D10)

N[d2] 계산 : 셀(D13) = NORMSDIST(D11)

이론가 계산 : 셀(D14) = D3*D12-D4*EXP(-F6*F5)*D13

계산 결과 행사가격 280의 콜옵션의 가격은 2.7968로, HTS 상의 2.73과 근접하게 나왔다. 약간 차이가 나는 부분은 오차 정도로 이해할 수 있다. 예를 들어 잔존 기간을 정확히 18일로 계산할 것인가, 금일은 이미 반이 지났으므로 17.5일로 적용할 것인가 하는 등의 문제로 약간의 차이가 날 수 있다.

이번에는 KOSPI200의 가격과, 잔존 기간을 변화시켜 가면서 콜옵션의 가격을 계산해 보자. 콜옵션의 가격은 S와, t의 함수, C(S,t), 이므로 두 변수의 변화에 따라 콜옵션 가격이 달라지므로, 그 특성을 그래프로 확인해볼 수 있다.

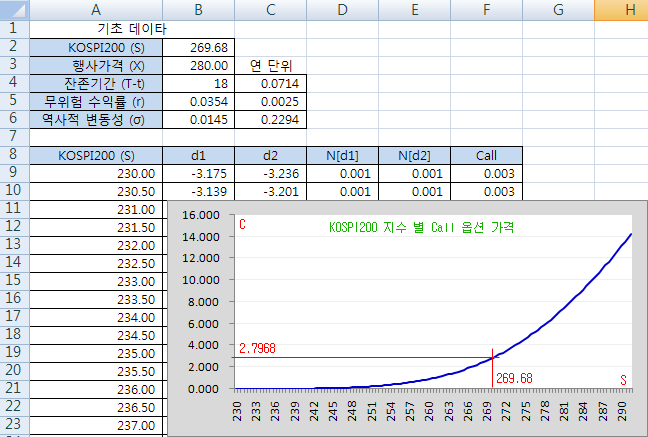
아래 그림은 잔존 기간을 18일로 고정하고, KOSPI200 가격 (S)을 230.00부터 0.5씩 증가시켜 가면서 계산한 콜옵션의 가격 그래프이다. S=269.68일 때의 이론가는 2.7968 이다. S가 250 까지는 거의 0에 가깝다가, S가 대략 270 부근부터는 급격히 상승하고 있다. 이것은 콜옵션이 지니는 볼록성 때문이며 S에 따라 기울기가 달라진다. 이 기울기는 나중에 자세히 언급하겠지만 옵션의 델타를 의미한다.

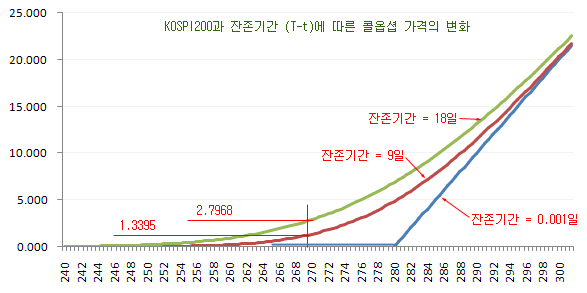
아래 그림은 위의 계산에서 잔존 기간을 18일, 9일, 0.001일로 바꾸어 가면서 그린 그래프이다. 동일 S값에 대해 잔존 기간이 많이 남은 콜옵션의 가격이 더 높은 것을 알 수 있다. S가 269.68일 때 잔존 기간이 18일 남은 콜옵션의 가격은 2.7968이고, 9일 남은 콜옵션의 가격은 1.3395이다. 기초자산의 가격이 변하지 않아도 잔존 기간이 짧아지면 옵션의 가격이 작아지는 것이다. 이것은 시간가치의 하락을 의미하며, 시간가치를 나타내는 세타값에 대해서도 나중에 자세히 언급하도록 하겠다.

알고리즘 트레이딩에서는 옵션의 이론가, 델타, 세타 값들을 빈번히 계산하게 된다. 특히 장중에 KOSPI200 지수는 물론이지만, 잔존 기간도 연속적으로 감소하기 때문에 이를 고려하여 델타나 세타 등을 계속 업데이트해 주어야 한다. 특히, 옵션의 양매도 전략 같은 곳에서는 세타 값이 대단히 중요하기 때문에 시간이 경과함에 따라 계속 재계산을 해 주어야 한다 (HTS에서 잔존 기간을 연속적으로 감소시키면서 재계산 해 주는지는 확인하지 못했습니다). 이 때 위의 계산법을 활용하면 도움이 많이 될 것이다 (델타, 세타는 나중에 자세히 언급하도록 하겠습니다).

[출처]6. 블랙 숄즈 공식의 활용 – 엑셀 연습|작성자아마퀀트