News & Events
금융 수학 (8)
코스피지수의 몬테카를로 시뮬레이션 (엑셀 계산)
[update 2016.11.24] 아래 수식은 주가모형의 시뮬레이션과 ELS 상품의 이해 (3) 에 동영상으로 설명되어 있습니다.
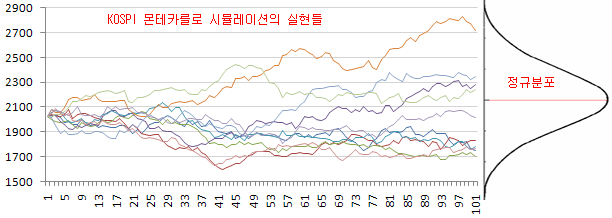
이전 포스트에서 기하 브라운 운동으로 만든 주가 모형을 이용하면, 미래 주가에 대한 시뮬레이션을 해볼 수 있다. 주가 모형에 대한 확률분포를 이용하여 몬테카를로 시뮬레이션이라는 기법을 적용해 보면 아래 그림과 같이 시뮬레이션을 해볼 수 있다. 아래 그림은 2012년 3월 23일 현재부터 100일 후의 KOSPI 지수를 10회 시뮬레이션 해본 결과이다. 현재의 변동성 (역사적 변동성 : HV), 연간 KOSPI 지수의 평균 수익률 등의 확률요소를 이용하여 100일 후의 주가를 예측해 보는 것이다. 시행 횟수가 많아지면 100일 후 주가의 분포는 정규분포를 나타낼 것이고, 정규분포 상에서 신뢰구간을 정하면, 주가의 폭 (밴드)을 예측해 볼 수 있다.
몬테카를로 시뮬레이션 기법을 적용하기 위해, 주가의 모형을 분석해 보자. 아래 식은 이전 포스트에서 설명한 주가의 수리적 모델이다. 식 4) 까지가 평균 수익률을 계산한 것이고, 식 5) 는 수익률에 대한 정규분포 특성을 나타낸 것이다. 주가의 로그 수익률 분포는 평균과 분산이 식 5)와 같이 되는 정규분포로 나타나고, 주가는 로그 정규분포 (Log Normal Distribution)로 나타난다. 식 3)에서 주가의 로그 수익률은 평균에서부터 표준편차의 위너 과정 (W)배 만큼 떨어진 지점으로 표현할 수 있고, 그림으로 그려보면 아래 그림과 같이 표현할 수 있다. 위너 과정 (W)에 따라 주가의 로그 수익률이 확률적으로 나타나는 것이다.
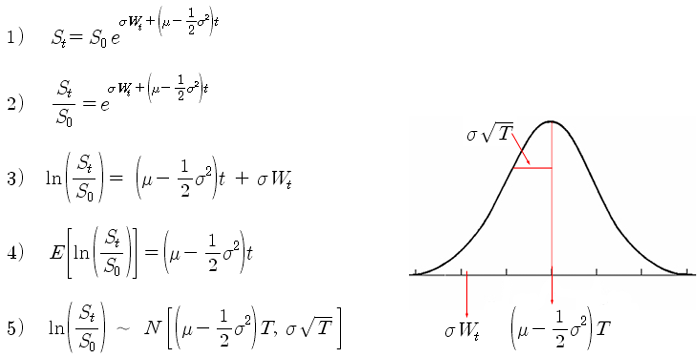
위의 식을 이용하면 엑셀에서 간단히 시뮬레이션을 해볼 수 있다. 주가의 연간 평균 수익률 (Drift 혹은 성장률)을 10%로 가정하고, 최근의 연간 변동성 (HV : 역사적변동성)은 금일 HTS에 표시된 20.59%를 기준으로 계산해 보았다. 일일 데이터로 100일간 시뮬레이션 할 것이므로, 수익률과 변동성은 모두 일일을 기준으로 단위를 조정한다 (단위를 맞추는 것이 대단히 중요하다). 각 셀의 계산식은 아래와 같다.
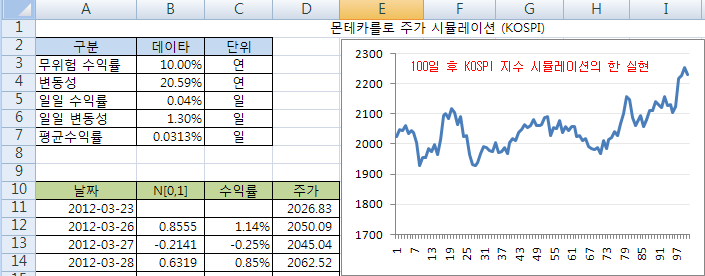
* 셀(B5) = 셀(B3) / 252
셀(B6) = 셀(B4) / sqrt(252) <– 일일 변동성으로 변환할 때 루트(t)를 이용
셀(B7) = 식 4)로 표현된 평균 수익률 (정규분포의 중심) = B5 – 0.5 * B6^2
~ 일일 단위이므로, t = 1
셀(B12) ~ 셀(B111) = NORMSINV(RAND())
~ 확률 0 ~ 1을 랜덤값으로 가질 때 표준 정규분포의 x축의 값이 나옴
~ ex: 확률이 0.5 지점이면 중심값이므로, NORMSINV(0.5) = 0
확률이 0.975 이면 2 시그마 지점이므로, NORMSINV(0.975) = 2
셀(C12) = 식 3)으로 표현된 로그 수익률 = $B$7 + $B$6 * B12
셀(C13) = $B$7 + $B$6 * B13
.
.
셀(D11) = 2026.83 <– 2012년 3월 23일 코스피 종가
셀(D12) = D(11) * EXP(C12)
셀(D13) = D(12) * EXP(C13)
.
.
각 셀을 위와 같이 계산하고, 열(D)인 예측 주가를 그래프로 그리면 위의 그래프가 된다. F9 키를 눌러 RAND() 값을 재계산하면 그래프의 모양이 계속 바뀌면서 시뮬레이션이 된다. 이 그래프는 한 실험에 대한 실현 (Realization)이므로, 여러 개의 실현을 만들어서 그래프를 겹쳐 그려보면 맨 위의 그래프가 나온다.
여기까지 한 개의 실험에 대한 실현값을 구해 보았다. 실제로 의미 있는 시뮬레이션이 되려면 실험의 횟수를 증가 시켜야 한다. 아래의 실험은 위의 실험을 4,000번 수행하여, 100일 후의 종가만 계산한 후 종가에 대한 히스토그램을 그린 것이다 (히스토그램 그리는 방법 참조).
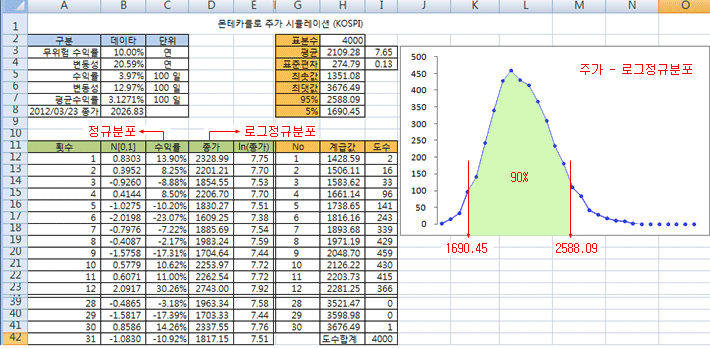
* 셀(B5) = 100 * B3/252 <– 100일간 Drift
셀(B6) = sqrt(100) * B4 / SQRT(252) <– 100일간 변동성
셀(B7) = B5 – 0.5 * B6^2 <– 식 4) 평균 수익률
셀(B12) = NORMSINV(RAND())
셀(C12) = $B$7 + $B$6 * B11 <– 100일간 로그 수익률 (예측치)
셀(D12) = $B$8 * exp(C12) <– 100일후 예상 주가 (연속 복리)
셀(D13) = $B$8 * exp(C13)
셀(E12) = ln(D12)
셀(E13) = ln(D13)
각 셀을 위와 같이 계산한 후 열(D)의 100일 후 종가에 대해 히스토그램을 그리면 우측의 그림과 같이 된다. 수익률 분포는 정규분포이지만, 주가의 분포는 로그정규분포의 모양으로 왼쪽으로 약간 기울어진 것을 볼 수 있다. 평균은 2,109.28 으로 B8*exp(B7)로 구한 평균값인 2,091.21과 비슷한 결과가 나왔다. 이 분포에서 신뢰구간을 90%로 하면, 100일 후 코스피 종가는 1,690 ~ 2,588 사이에 분포할 확률이 90%가 된다고 할 수 있다.
* 셀(G3) : 100일 후 종가의 평균 = AVERAGE(D12:D4011)
셀(G4) : 100일 후 종가의 표준편차 = STDEV(D12:D4011)
셀(I3) : 100일 후 로그 종가의 평균 = AVERAGE(E12:E4011)
셀(I4) : 100일 후 로그 종가의 표준편차 = STDEV(E12:E4011)
셀(G7) : 로그정규분포의 95% 지점 = LOGINV(0.95, I3, I4) = 2,588.09
셀(G8) : 로그정규분포의 5% 지점 = LOGINV(0.05, I3, I4) = 1,690.45
몬테카를로 시뮬레이션에 의한 100일 후 코스피 지수의 평균값은 2,091이고, 예측 범위는 1,690 ~ 2,588로 나왔다 (90% 신뢰구간). 현재의 코스피 지수는 2,027인데, 연간 코스피의 성장률을 10%로 대입하였기 때문에 100일 후 코스피가 2,091부근에서 나온 것은 당연한 결과이다. 그리고 평균을 중심으로 한 밴드는 역사적변동성 (HV) 20.59%의 영향을 받게 된다. 따라서 예측 결과는 두 값 모두에 의해 영향을 받게 된다. 만약 코스피 성장률과 연간 변동성을 보다 정확하게 예측할 수 있다면, 시뮬레이션 결과도 더 정확해 질 것이다.
코스피의 연간 성장률은 경제동향과 밀접한 관련이 있으므로, 거시경제적 측면의 분석이 필요할 것이다. 또한, 변동성은 역사적 변동성 (HV) 대신에 옵션의 시장가격을 통해 얻은 내재변동성 (IV : Implied Volatility)을 이용하거나, 시계열분석 기법으로 예측된 변동성을 이용할 수도 있다.
예를 들어 역사적 변동성 (HV)대신 내재변동성 (IV)를 이용해 보자. 내재변동성은 옵션시장에서 참가자들에 의해 형성된 옵션의 가격을 통해 측정해 본 기초자산 (KOSPI200)의 변동성이다. 금일 HTS 상에는 IV = 15.00%로 기록되어 있다. 이 값을 사용하면 100일 후 코스피 지수의 평균값은 2,093 이고, 예측 범위는 1,780 ~ 2,406 이 나왔다. 평균은 성장률 (Drift)에만 영향을 받으므로 변화가 없고, 예측 범위는 변동성의 영향을 받아 폭이 약간 좁아졌다.
여기서는 기본적인 데이터를 사용해서 원리만 살펴본 것이므로 예측 밴드의 폭이 상당히 넓게 나온 편이다. 가끔 증권사에서 발표하는 예측 지수의 범위도 이러한 원리로 계산되었을 것이다.


