[페어 트레이딩/고급편] 10. 진입선의 최적화 알고리즘

페어트레이딩 (Pairs Trading) – 고급(10)

진입선의 최적화 알고리즘 (Profit Profile)   

페어트레이딩을 하다 보면 어느 지점에서 진입하는 것이 좋을지 매번 생각하게 된다. 기계적인 트레이딩을 위해서는 기준점을 설정하는 것도 좋은 방법인데, 어느 지점을 기준으로 삼아야 할지 항상 고민이 된다.

비율 스프레드로 페어트레이딩을 설명해 놓은 책들에서는 스프레드의 2*표준편차 지점을 진입선으로 사용하곤 한다. 이것은 스프레드의 분포가 표준 정규분포임을 가정하여 95%의 확률 범위를 벗어난 지점을 이상 현상으로 판단하여 진입선으로 활용하고 있는 것이다. 페어트레이딩의 대상으로 선정된 페어라면 스프레드의 분포는 대충 정규분포에 가까우므로, 이것도 괜찮은 방법이긴 하다. 그러나 페어마다 스프레드의 특성이 조금씩은 다르기 때문에, 모든 스프레드에 일률적으로 2*표준편차를 적용하는 것이 타당한지는 생각해 볼 문제이다.

여기서는 스프레드의 모양과 진입선의 위치가 수익률에 어떤 영향을 주는지를 따져보고, 최적의 진입선을 선정하는 방법에 대해 알아보도록 한다.

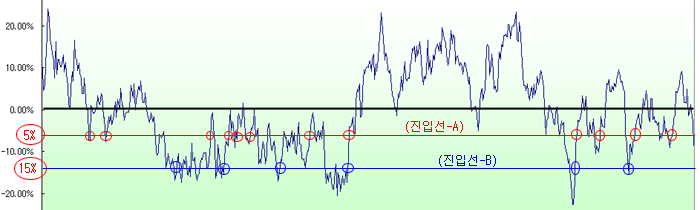
위의 그림은 일반적인 형태의 스프레드 차트이다. 진입선에서 진입하고, 균형점에서 청산하는 것을 가정하고, (진입선-A)와 (진입선-B)를 비교해 보자. (A)는 균형점으로 회귀할 경우의 기대 수익률이 5%인 지점이고, (B)는 15%인 지점이다. (A)에서 진입하면 기대 수익률은 작지만 진입횟수가 늘어난다. 반면에 (B)는 진입횟수는 적지만 기대 수익률은 늘어난다.  (A)의 총 기대 수익률은 기대 횟수 * 기대 수익률 = 12 * 5% = 60% 가 되고, (B)는 6 * 15% = 90% 가 된다. 위의 그림은 2.5년 동안의 스프레드이므로, 연간으로 환산하면 (A) = 24%, (B) = 36% 가 된다. 그러면 이 형태의 스프레드는 (진입선-B)가 더 유리하다는 것을 알 수 있다. 물론 이것은 과거의 결과적인 상황이고 앞으로도 그러리라는 보장은 없다. 다만 과거 사실을 통한 참고 자료인 것이다.

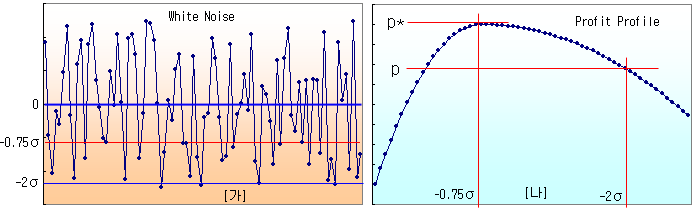
위 그림의 [가]는 White noise의 정상 시계열이다. White noise를 스프레드로 생각하고 진입선을 아래로 이동해 가면서 기대 수익률을 계산해 보면 (진입선 = 0, -0.1σ, -0.2σ … ), 수익률 (Profit)과 진입선 (표준편차)사이의 관계는 그림 [나]와 같이 된다 (Profit Profile). 어느 지점까지는 수익률이 증가하다가, 어떤 지점을 지나가면 수익률이 감소하고 있다. 즉, 수익률이 최대가 되는 지점이 존재한다는 것이다. White noise의 경우 최적점은 표준편차의 0.75배 되는 지점으로 알려져 있다.

이 원리를 이용하면 페어트레이딩의 최적 진입선을 구해 볼 수 있다. 수학적으로 계산하는 것이 아니라 컴퓨터 알고리즘으로 찾아 볼 수 있다. 진입선을 균형점에서부터 아래로 0.1%씩 (더 작게 해도 된다) 줄여 나가면서 총 기대 수익률을 계산해 본다. 이때 총 기대 수익률이 최대가 되는 지점을 찾으면 이 지점이 최적 진입선이 된다.

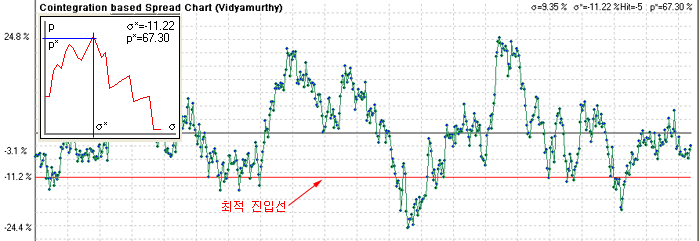
아래는 알고리즘으로 찾아본 최적 진입선의 예이다. 첫 번째 예는 한화케미칼과 케이피케미칼의 스프레드 차트이다. 최적 진입선은 -11.2% 이고, 총 기대 수익률은 연간 27% (67.30% / 2.5) 였다. Profit Profile 차트를 보면 진입선이 -11.2% 보다 작거나 크면 수익률이 감소하는 것을 알 수 있다.

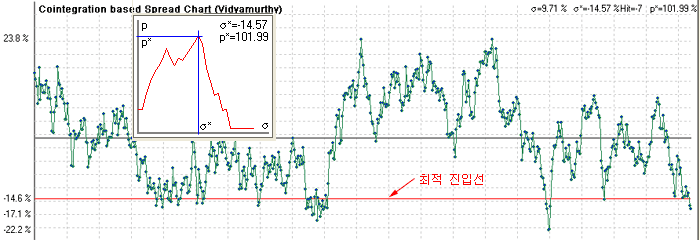
아래는 현대모비스와 한라공조의 스프레드 차트이다. 최적 진입선은 -14.6% 지점이고, 수익률은 연간 35% 였다. 진입선이 -14.6% 보다 작거나 크면 수익률이 감소하고 있다.

이 결과는 과거의 고정된 상황으로부터 얻어진 것이다. 사실, 시간이 지남에 따라 분석 기간의 데이터가 달라지기 때문에 스프레드와 균형점에는 미세한 변화가 생긴다. 이런 점까지 고려한다면 위의 결과도 당연히 달라지게 될 것이다. 여기서는 단순히 고정된 상황에서의 진입선과 수익률 간의 관계를 살펴본 것이다.

위의 논리로 구한 최적 진입선을 얼마나 신뢰할 것이냐 하는 문제는, 투자자의 투자성향과 관계가 있다. 단기 투자자의 경우에는 진입선 보다 위에서도 진입할 수 있고, 조금만 올라도 청산할 수가 있다. 장기 투자자라면 진입선 보다 아래에서 진입하여 충분히 기다렸다가 균형점보다 위에서 청산할 수도 있다. 전자의 경우는 빈번한 거래 비용을 지불해야 할 것이고, 후자의 경우에는 시간 비용을 지불해야 할 것이다. 따라서 최적 진입선은 모두 투자자에게 적합한 것은 아니며, 참고 자료인 보조 지표로 활용될 수 있다.

[출처]10. 진입선의 최적화 알고리즘|작성자아마퀀트