News & Events
[페어 트레이딩/고급편] 13. Cointegration 계수와 균형점의 관계
- 2019년 1월 7일
- Posted by: 인사이트캠퍼스
- Category: 금융/AI/IT 기사

페어트레이딩 (Pairs Trading) – 고급(13)
Cointegration 계수와 균형점의 관계
페어트레이딩에서는 스프레드의 균형점 (Long-run equilibrium)으로 스프레드의 전체 평균값을 이용한다. 스프레드가 위, 아래로 움직이면서 평균점으로 회귀하는 성질이 있기 때문에 평균값을 균형점으로 본다. 또한 페어트레이딩에서는 서로 떨어져 있던 두 주가가 어디서든 만나기만 하면 차익이 발생하는데, 주가가 만나는 지점과 균형점과는 어떤 관계가 있는지 의문이 든다. 직관적으로는 두 주가가 균형점에서 만날 것으로 예상되는데 실제로는 어떤지 확인해보자. 결론은 두 주가가 반드시 균형점에서 만나는 것이 아니라, Cointegration 계수 (CC)에 따라 만나는 지점이 달라진다는 것이다.
두 주가가 만나는 지점을 확인하기 위해 아래 수식을 이용한다. 식 1)은 (고급편) 5. 스프레드와 수익률에서 언급한 스프레드와 수익률의 관계식이다. 이 식을 변형하여 균형점인 S2 = 0 인 지점에서의 CC와 수익률, 그리고 스프레드의 관계를 구해보면 식 3)과 같이 된다.

현재 균형 상태에서 S1 만큼 떨어져 있는 두 주가 A와 B를 생각해 보자. A가 저평가 상태에 있고, B가 고평가 상태에 있다고 가정한다. 그럼 A를 매수하고, B를 CC배 만큼 매도하는 상황이 된다. 여기서 두 주가가 만나는 지점에 대해 살펴보려고 한다. 두 주가를 한 공간에 같이 그릴 때 시작점을 일치시킬 것인지, 다른 어떤 곳을 일치시킬지 여부에 따라 떨어져 있는 정도가 다르므로, 주가의 위치를 실제 그림으로 표현할 수는 없다 (현재 S1 만큼 떨어져 있고, 누가 고평가인지, 저평가인지라는 사실만 알 뿐이다). 따라서 두 주가의 위치는 추상적인 개념으로 이해해야 한다. 변동성을 표준화한 정규화 가격지수 (Normalized Price)를 이용하는 것이 보통이다. (기초편) 3. 정규화 가격지수 참조.
1. 균형점에서 만나는 경우
스프레드가 S1 만큼 떨어져 있는 두 주가 A와 B가 균형점에서 만나는 경우는 아래 그림과 같이 세 가지가 있다. 첫 번째 경우는 B는 하락하고, A는 상승하는 경우이다. B는 매도 포지션 이므로 A,B 모두 수익이 발생한 경우이다. 두 번째 경우는 B가 상승하여 손실이 발생하고, A는 상승하여 이익이 발생한 경우이다. 세 번째 경우는 B가 하락하여 이익이 발생하고, A는 하락하여 손실이 발생한 경우이다. 세 경우 모두 |S1| 만큼 차익이 발생한다.
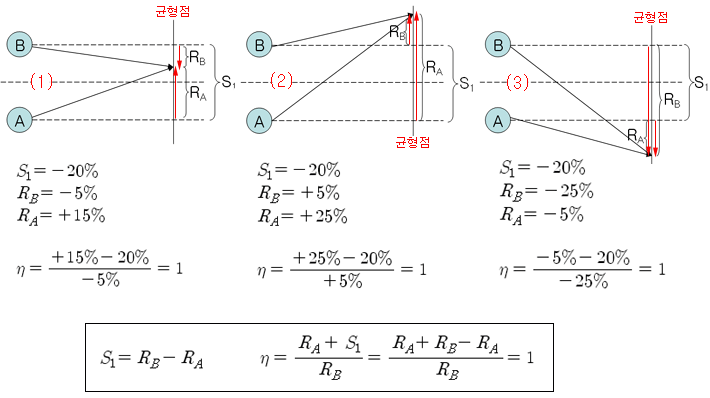
위의 세 경우에 대해 위에서 언급한 식 3)으로 CC를 계산해 보면, 모두 1 이 나온다 (RA, RB, S1이 크기와 방향을 가진 벡터량이므로 부호가 혼돈되어 숫자를 직접 대입하여 계산하였음). 즉, 떨어져 있는 두 주가가 균형점에서 만난다면 모든 경우에 대해 CC = 1이 된다. 거꾸로 말하면 CC = 1 이면 두 주가는 균형점에서 만날 것으로 기대된다 (필요충분 조건임).
2. 균형점보다 아래에서 만나는 경우
두 주가 A,B가 균형점보다 아래에서 만나는 경우는 아래 그림과 같다. 계산 결과, 조건에 따라 CC < 1 인 경우도 있고, CC > 1 인 경우도 있다.
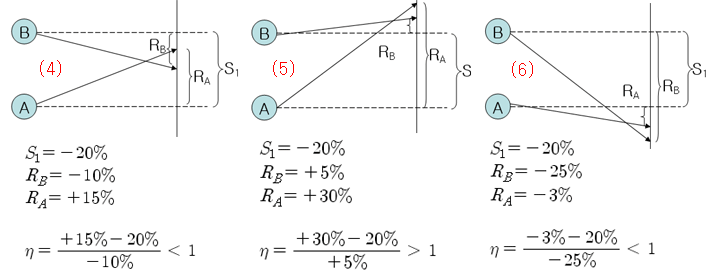
3. 균형점보다 위에서 만나는 경우
두 주가 A,B가 균형점보다 위에서 만나는 경우는 아래 그림과 같이 된다. 이 경우 역시 CC > 1 인 경우도 있고 CC < 1 인 경우도 있다.
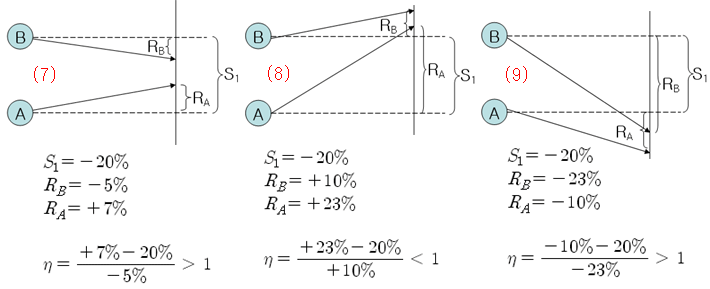
위에서 살펴본 바와 같이 CC = 1 이면 A, B의 등락 방향이나 등락폭에 관계없이 균형점에서 만나고, CC 가 1 보다 크거나 작으면 등락 방향과 등락폭에 따라 균형점의 위나 아래에서 만난다. CC가 1에 가까울수록 점점 균형점 가까이에서 만난다고 유추할 수도 있다. 또한 (고급편) 4. 페어트레이딩의 위험 측정에서 살펴보았듯이 CC = 1일 때가 위험이 가장 작게 측정된다. 그렇다면 두 주가가 만나는 지점이 균형점에 가까울수록 위험이 작아진다고 말할 수 있다.
위의 경우를 요약하여 아래 테이블에 다시 표시해 보았다. CC가 1이 아닌 경우에는 조건에 따라 만나는 지점이 다르다. 조건에 따라 결과가 달라, 통일된 모양의 조건을 만들지는 못하였다.
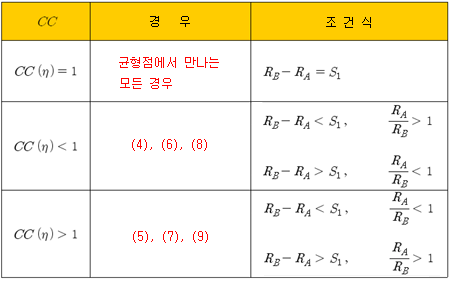
이번 포스트에서는 떨어져 있는 두 주가가 어디쯤에서 만날지에 대해 생각해보았다. 명쾌하게 어디쯤에서 만날 확률이 어는 정도 된다는 결론을 내지는 못하였지만, CC와 균형점의 관계에서 어떤 조건일 때 어디서 만날 것을 기대하는지 어렴풋이나마 살펴보았다.
참고로, 페어트레이딩에서 스프레드에 대한 의문점으로 중요한 것을 꼽아보면 아래와 같을 것이다.
1.이 스프레드가 페어트레이딩에 적합한 것인가?
2.현재 스프레드는 얼마만큼 떨어져 있는가?
3.향후 스프레드가 어디쯤에서 좁혀질 것인가 (두 주가가 어디서 만날 것인가)?
4.언제쯤 스프레드가 좁혀질 것인가 (두 주가가 언제 만날 것인가)?
1~3 까지의 의문은 그동안의 포스트에서 조금씩이나마 다루어 보았다. 그러나 4번의 의문에 대해서는 접근해보지 못했다. 이 문제에 대해서는 현재도 Stochastic Pairs Trading 이라는 주제의 논문들이 많이 발표되고 있는데, 그 안에서 이 문제 (기대 기간)에 대해 언급하고 있는 것들이 있다. 이 분야는 필자의 수준을 넘어선 것이라 여기서는 소개할 수가 없어 아쉬운 면이 있다. Stochastic Calculus에 능한 독자라면 한 번 도전해 보길 바란다. (저는 지금 “Stochastic Calculus for Finance by Steven E. Shreve” 를 공부하고 있는데, 아직 초보 수준이라 시간이 많이 걸리고 있습니다. 나중에라도 알게 되면 추가해 보도록 하겠습니다.)

