News & Events
[페어 트레이딩/고급편] 18. 공통추세모형 (Common Trend Model)
- 2019년 1월 7일
- Posted by: 인사이트캠퍼스
- Category: 금융/AI/IT 기사

이전 시간에는 공적분 계수 (Cointegration Coefficient)를 추정해 보았고, 이것을 페어트레이딩의 최적 투자 비율로 적용해 보았다. 추정 방법은 아래 식 4)에서 계산된 스프레드의 정상성 (Stationary)이 최대가 되는 h 를 추정한 것이었다. 정상성이 최대가 된다는 것은 자기상관계수 (Auto-correlation)가 최소가 된다는 것이므로 (다음 시간에 살펴볼 것임), 스프레드의 자기상관계수가 최소가 되는 h 를 추정하였다. 추정된 h가 바로 공적분 계수이고, 동시에 페어트레이딩의 최적 투자비율이었다.
이번 시간에는 왜 이런 논리가 성립하는 지에 대해 알아보기로 한다. 아래 식은 시장중립모형 (Market Neutral Model)에서 살펴본 스프레드의 전개식이다. 페어트레이딩 포트폴리오의 수익률은 식 1)과 같이 표현할 수 있고, h 는 헤지비율로 생각할 수 있다. 종목-A와 종목-B의 수익률을 로그 수익률로 나타내면 식 2)와 같이 되고, 스프레드는 식 4)로 표현할 수 있다.

여기서 최적 헤지비율인 h를 결정하는 것이 관건이다. 시장중립모형에서는 각 종목의 수익률에 CAPM의 시장모형을 적용하여, 각 종목의 베타로 h 를 결정하여 시장중립 포트폴리오를 만들었다. 그러나 이 방법은 각 종목의 수익률이 CAPM의 시장모형을 따른다는 가정이 필요하고, 종목별로 베타가 (어느 정도는) 일정하다는 가정이 필요하다. 따라서 종목 베타를 사용하여 h 를 추정한다는 것은 가정에 의한 오차 (Assumption Error)가 발생할 가능성이 있다.
이번에는 위의 가정 없이 최적의 h 를 추정하는 방법에 대해 살펴보기로 한다. 아래와 같이 추세가 유사한 종목-A의 주가와 종목-B의 주가를 생각해 보자. 종목-A에만 투자한다면 추세에 대한 위험 (Trend Risk)이 존재할 것이다. 만약, B 의 추세가 A 의 추세와 유사하다면, A 를 매수하고, 동시에 B 를 매도한다면 추세가 서로 상쇄되어 추세에 대한 위험이 감소할 것이다. 만약, 두 추세가 완전히 동일하다면 추세위험은 완전히 상쇄될 것이다.
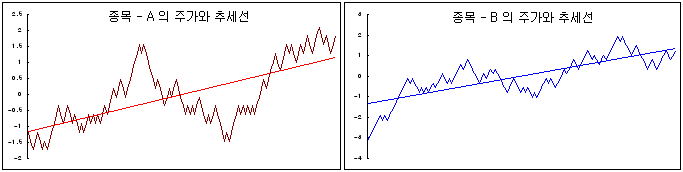
A와 B 사이에 공통적으로 존재하는 추세를 공통추세 (Common Trend)라 한다. 두 종목 사이에 공통추세가 존재하고, A, B 주가를 공통추세와 기타 잔차 성분으로 분해할 수만 있다면, A,B 사이의 공통추세를 쉽게 확인할 수 있다. 그러나 공통추세는 추상적인 개념이라 분리해내기는 쉽지 않다. 만약 분리가 가능하다면 각 추세의 비율을 계산해서, 이것을 헤지비율로 적용하면 공통추세가 제거되고 잔차 성분만 남을 것이다. 그리고 남은 잔차 성분의 정상성은 높아질 것이다 (순수 잔차의 정상성은 대단히 높음, ex : 백색잡음 (White Noise)). 만약 공통추세가 완전히 제거되지 않는다면 남은 잔차 성분의 정상성은 낮아질 것이고, 제거되지 못하고 남아있는 추세는 위험 요인이 된다.
* A,B 공통추세 존재 –> 공통추세 완전 제거 –> 남은 잔차의 정상성이 높아짐
* A,B 공통추세 존재 –> 공통추세 부분적 제거 –> 추세성분이 남아있음 –> 잔차의 정상성이 낮아짐
아래 그림은 이전 시간에 계산해 본 KT-SKT 의 스프레드 차트이다. 왼쪽 그림은 공통추세가 완전히 제거되지 못하고 잔차 (스프레드) 성분에 추세가 존재하는 경우이고, 오른쪽 그림은 공통추세가 완전히 제거되어 잔차 (스프레드) 성분에 추세가 남아있지 않은 경우이다. 따라서 왼쪽이 오른쪽보다 추세위험이 더 높다는 것을 알 수 있다.
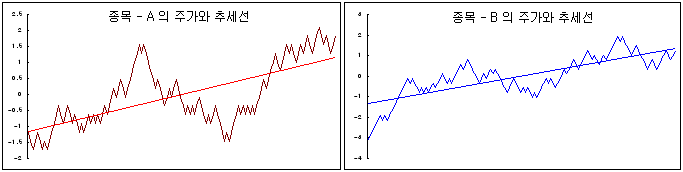
이번에는 종목-A와 B의 차트를 아래 그림과 같이 겹쳐서 그려보자. 두 추세선이 유사하긴 하지만 정확히 일치하지는 않는다. 따라서 두 주가의 헤지비율을 1:1로 적용하여 스프레드를 그려보면 추세 성분이 완전히 제거되지는 못할 것이다. 그러나 한 쪽 추세선의 기울기에 얼마를 곱해 준다면 두 추세선을 일치시켜 볼 수 있다. 여기서 추세선의 기울기를 일치시키기 위해 곱해주는 값을 헤지비율로 생각해 볼 수 있다. (단, 추세선은 추상적인 개념의 공통추세를 의미하는 것이며, 단순히 회귀직선과 같은 추세선을 의미하는 것은 아니다. 또한, 대부분 공통추세는 직선의 형태로 표현되지도 않을 것이다.)
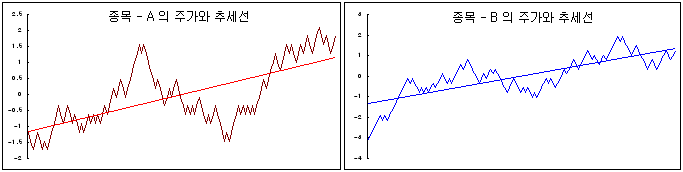
예를 들어, 종목-B 추세선의 기울기에 h=0.8 을 곱하면 종목-A 추세선의 기울기와 일치한다고 가정해 보자. 그리고 위의 식 4)를 이용해서 스프레드 (잔차 성분)를 계산해 보자. 만약 계산된 스프레드에 추세가 없고 정상성이 높다면, 공통추세가 제거된 것으로 볼 수 있다. 공통추세가 존재하고, 공통추세를 제거한 잔차 성분에 추세가 없는 정상성이 존재한다면, A 와 B 는 공적분 관계에 있는 것이고, 공적분 계수는 h=0.8이 된다.
동일 업종에 해당하는 두 종목은 공적분 관계에 있을 가능성이 높으므로, 계산된 스프레드에 추세가 없고 정상성이 최대가 되는 계수를 수치해석으로 찾아내면, 이 값이 바로 공적분 계수가 될 수 있고, 최적 투자 비율이 될 수 있다. 이전 포스트에서 공적분 계수를 추정한 절차가 바로 이 논리를 적용한 것이다. 만약 정상성이 최대가 되는 계수는 찾았지만, 스프레드에 추세가 존재하고, 정상성이 낮다면, 찾은 계수는 공적분 계수가 될 수 없고, 궁극적으로는 두 종목에는 공적분 관계가 존재하지 않는다는 것을 의미한다. 따라서 두 종목은 페어트레이딩의 대상이 될 수 없다.
결론적으로 페어트레이딩의 최적 투자 비율의 결정은, 베타를 사용한 시장모형 (CAPM)보다, 공적분 계수를 사용한 공통추세모형 (Common Trend Model)을 적용하는 것이 더 효과적이라 할 수 있다.
이번 시간에는 스프레드에 추세가 없고 정상성이 최대가 될 때의 비율이 공적분 계수가 된다는 것을 알아보았다. 다음 시간에는 스프레드의 정상성과, 자기상관계수의 관계에 대해 알아보기로 한다. 이것을 이해하기 위해서는 시계열분석의 AR (Auto Regressive) 과정을 이해할 필요가 있다. 이 부분에 대해서는 다음 시간에 자세히 알아보기로 한다.

