[페어 트레이딩/고급편] 21. 다중 페어트레이딩 (2)

페어트레이딩 (Pairs Trading) – 추가편(5)

다중 페어트레이딩 (2)

이전 시간에는 지주사-계열사와 같은 형태의 다중 페어트레이딩에 대해 생각해 보았었다. 이번 시간에는 3 종목이 서로 독립적으로 관계를 맺고 있는 경우의 다중 페어트레이딩에 대해 생각해 본다. 이런 경우의 예는 동일 업종에 속해 있는 3개의 종목, 3개의 지수 선물 (국가 간 : KOSPI 선물 – S&P 500 선물 – Nikkei 선물, 국내 : KOSPI 선물 – 원달러 선물 – 국채 선물), 혹은 3개의 상품 선물 (Commodity Futures : 옥수수 – 콩 – 밀) 등 매우 다양하다.

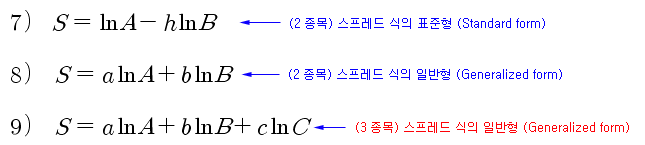
다중 페어트레이딩을 위해서는 그동안 다루어 왔던 표준적인 페어트레이딩의 식을 (표준형) 일반적인 표현으로 (일반형) 확장해 볼 필요가 있다. 아래의 식 1) 은 3 종목으로 구성된 포트폴리오의 수익률 표현이다. a,b,c 가 각각의 가중치 일 때, 포트폴리오의 수익률은 각 종목 수익률의 가중 평균이 된다. 또한 a,b,c 는 매수/매도에 따라 양수가 될 수도 있고, 음수가 될 수도 있다.

식 1)의 수익률을 로그 수익률로 표현하면 식 2)와 같이 된다. 스프레드 식을 식 4), 5)와 같이 정의하면, 포트폴리오의 수익률은 식 6)과 같이 스프레드의 차로 표시할 수 있다. 여기서 식 4) 혹은 5)가 일반화된 스프레드 식이 된다. 식 7)은 그동안 다루어 왔던 스프레드 식의 표준형이다. 이 식은 종목 A의 투자비율을 1로 고정한 상태에서 종목 B의 투자비율을 결정하기 위한 식 이었다. 식 8)은 식 7)에 대한 일반적인 표현이다. 이 식은 종목 A의 투자비율을 1로 고정하지 않고 A와 B의 투자비율을 (a와 b를) 각각 결정하기 위한 식이다. 식 8)의 일반적인 표현을 식 9)로 확장하면 3종목에 대한 스프레드의 일반적인 표현이 된다.

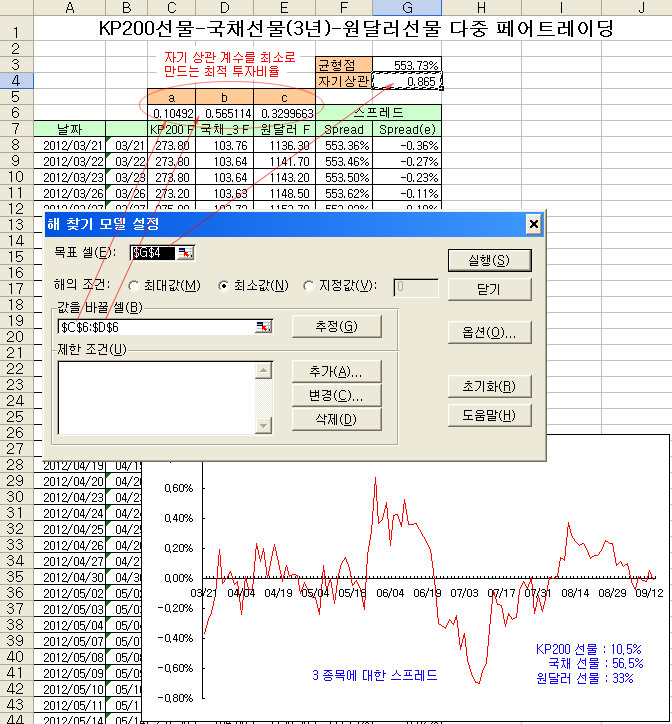
아래 그림은 KOSPI200 지수 선물과 국채 선물 그리고 원달러 선물을 묶어서 다중 페어트레이딩을 구성해 본 예 이다. 스프레드 계산은 식 9)를 이용하였고, 각 투자비율은 기존과 동일하게 스프레드의 정상성이 최대가 되는 조건, 즉, 스프레드의 자기상관계수가 최소가 되는 조건을 이용하였다. 스프레드의 표준형과 달리 공적분 계수가 단일로 존재하는 것이 아니라 각각의 비율로 분리된 형태이다 (a, b, c).

계산식 :

스프레드(셀 F8) = $C$6*LN(C8)+$D$6*LN(D8)+$E$6*LN(E8)

균형점 (셀 G3) = AVERAGE(F8:F129)

스프레드 잔차 (셀 G8) = F8-$G$3

자기상관계수 (셀 G4) = CORREL(G8:G128,G9:G129)

c (셀 E6) = 1-C6-D6

위와 같이 계산한 후 엑셀의 해찾기 기능을 사용하여 자기상관계수가 최소가 되도록 a와 b를 결정하고, c 는 1 – a – b 로 결정한다. 결과는 KOSPI200 지수 선물이 약 10.5%, 국채 선물이 약 56.5%, 그리고 원달러 선물은 약 33%가 나왔다. 이 비율을 사용하면 위의 그림과 같은 스프레드를 얻을 수 있다. 육안으로 보아도 정상성이 좋은 것으로 확인된다. y-축의 수익률이 비교적 작은 이유는, 3 종목의 상관관계가 매우 높기 때문에 괴리가 크게 발생하지 않기 때문이다. 또한, a,b,c가 모두 양수가 나온 것은 3 종목이 서로 음의 상관관계에 있기 때문이다. KP200 지수 선물이 상승할 때 원달러 선물은 하락하는 관계에 있기 때문에 진입시 매수/매도 포지션이 아닌, 매수/매수 포지션이 되어야 롱-숏 관계가 된다.

위의 비율로 각각 투자한다는 것은 위의 스프레드에 투자하는 것과 동일하므로 스프레드의 하단에서 진입하고, 상단에서 청산하면 y-축 만큼의 수익률을 기대할 수 있는 것이다. 다중 페어트레이딩도 스프레드의 정상성을 높게 만들었으므로 추세에 대한 위험이 없는 시장중립전략이 된다. 또한, 식 9)는 3 종목뿐만 아니라 4 종목, 5 종목 등으로 계속 확장해 나갈 수 있다.

[출처]21. 다중 페어트레이딩 (2)|작성자아마퀀트