[페어 트레이딩/고급편] 25. 공적분 몬테카를로 시뮬레이션 (2)

페어 트레이딩 (Pairs Trading) – 추가편 (9) 공적분 몬테카를로 시뮬레이션 (2)

페어 트레이딩은 과거의 주가를 이용하여 공적분 관계를 분석하며, 미래에도 이 관계가 유지된다는 것을 가정한다. 그러나 실제 투자를 하다보면 공적분 관계가 깨지는 경우를 종종 보게 된다. 즉, 페어의 스프레드가 충분히 떨어졌다고 판단하여 베팅을 하였으나, 스프레드가 더 떨어져서 손절을 하게 되는 경우가 많이 있다. 아마도 이것이 페어 트레이딩의 가장 큰 위험일 것이다.

그렇다면 향후 공적분 관계가 깨질 확률이 얼마나 되는지 추정해 볼 방법은 없을까? 미래의 공적분 관계를 예측할 수는 없지만, 공적분 계수의 분포를 추정해 보면 어느 정도는 확인해 볼 수 있을 것 같다. 공적분 관계가 깨진다는 것과, 공적분 계수가 달라진다는 것은 같은 의미로 볼 수 있다. 즉, 현재 시점에서 공적분 계수가 1.0 로 측정되었는데 (과거 데이터를 사용), 미래 시점에는 2.0으로 측정되었다면, 이 페어는 공적분 관계에 변화가 생긴 것으로 볼 수 있다. 따라서 미래 시점의 공적분 계수의 분포를 추정해 보면 공적분 관계가 깨질 확률을 추정해 볼 수 있다.

위의 그림은 공적분 계수의 분포를 만들기 위한 과정이다. 선정된 페어의 과거 주가를 이용하여 각각의 Drift (μ) 와 변동성 (σ), 그리고 이 페어의 공적분 계수 (cc)를 추정한다. 그리고 이 정보를 이용하여 공적분 몬테카를로 시뮬레이션을 여러 번 수행한다. cc=1.0 이라면  시뮬레이션은 cc가 최대한 1.0 이 되도록 두 주가의 패턴을 만들어 낼 것이다. 시뮬레이션 결과로 만들어진 두 주가로부터 다시 공적분 계수를 추정한다. 추정된 공적분 계수는 주가 모형의 불확실성항 때문에 cc가 정확히 1.0 이 되지는 않을 것이고, 분포를 형성하게 된다. 이 분포를 분석해 보면 향후 공적분 관계가 깨질 확률을 구해볼 수 있다.

아래 그림은 Drift가 각각 2.75% 이고, 변동성이 각각 20%, 그리고 공적분 계수가 cc=1.0인 두 주가의 관계를 1,000 번 시뮬레이션하고, 생성된 주가로부터 다시 공적분 계수를 추정하여 만든 공적분 계수의 분포이다. 공적분 계수의 평균은 1.01 로 지정한 1.0 과 잘 일치한다. 그러나 공적분 계수가 2.566 (Max)이 나온 경우도 있었고, 0.384 (Min)이 나온 경우도 있었다.

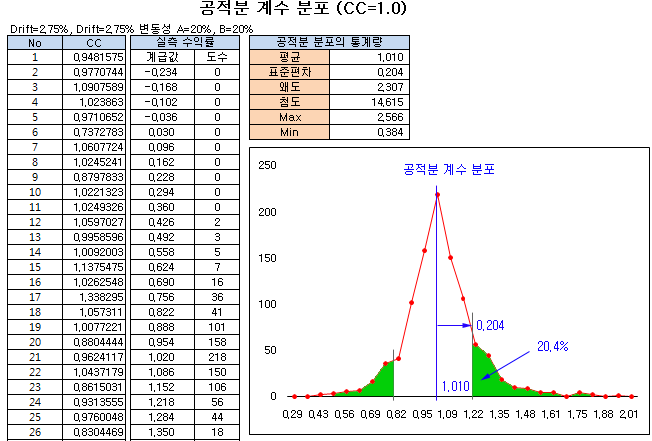
이 결과는 현재 두 주가의 공적분 계수가 1.0 이었더라도, 미래에는 0.384 ~ 2.566 범위에 존재할 수 있음을 보여준다. 만약, 공적분 계수가 ±1σ를 벗어나는 경우를 공적분 관계가 깨진 것으로 본다면, 이 확률은 20.4% 정도가 나온다. 즉, 공적분 계수를 1.0으로 기대했을 때, 이 값이 0.806 ~ 1.215 의 범위를 벗어날 확률은 20.4% 정도가 되는 것이다.

아래 그림은 Drift가 2.75%, 5.50% 이고, 변동성이 각각 20%, 그리고 공적분 계수가 cc=2.0인 두 주가의 관계를 1,000 번 시뮬레이션한 결과를 분포로 나타낸 것이다. 평균은 2.083 으로 지정한 2.0과 잘 일치한다. 분포의 표준편차는 0.493 으로 cc=1.0 일 때보다  높게 관측되었다. 그리고 공적분 계수가 ±1σ를 벗어나는 경우는 26.0% 로 공적분 계수가 1.0일 때 보다 더 높았다.

공적분 시뮬레이션은 두 주가가 균형점으로 회귀하도록 의도적으로 만든 것이므로, 대체적으로 공적분 관계가 잘 유지된다고 할 수 있다. 그럼에도 불구하고 주가의 불확실성으로 인해 공적분 관계가 깨지는 경우가 약 20% 정도 발생한다. 실제 시장에서 두 주가는 시뮬레이션보다 공적분 관계가 더 약할 수밖에 없다. 그 이유는, 당연히, 실제 시장은 의도적인 관계가 아니라 수요와 공급의 거래 시스템으로부터 만들어지는 자연스러운 관계이기 때문이다. 따라서 실제 시장에서는 향후 공적분 관계가 깨질 가능성이 시뮬레이션 결과인 20% 보다 더 높을 수밖에 없다.

페어 트레이딩은 분명히 통계적 차익거래에 속한다. 절대적 차익거래가 아닌 만큼 위험이 존재할 수밖에 없다. 위에서는 ±1σ의 범위를 가정했지만 ±0.5σ의 범위를 가정하면 공적분 관계가 깨질 확률은 무려 46%로 증가한다. 공적분 계수는 투자 비율을 의미하므로 공적분 계수가 변한다는 것은 기대수익률이 변한다는 것을 의미한다. 공적분 계수가 10% 변하면 수익률도 그 정도 변한다고 볼 수 있으므로, 위험의 크기가 그리 작은 편은 아니다.

페어 트레이딩에 대해 글을 쓰고, 강의를 하면서 많은 사람들과 대화를 나누다 보면, 페어 트레이딩에서 큰 수익을 기대하거나, 페어 트레이딩을 위험이 거의 없는 투자 기법으로 생각하는 사람들을 더러 보게 된다. 그러나 페어 트레이딩도 분명히 위험이 존재하고, 그 크기도 그렇게 작지  만은 않다는 사실을 인식할 필요가 있다. 물론, 방향성 투자보다 위험이 작은 것은 사실이다. Pairs Trading의 “s” 의미도 복수의 페어로 포트폴리오를 구축하여 그 중 일부는 공적분 관계가 깨져 손실을 보고, 나머지는 기대대로 수익을 내서 총 수익률이 “+” 가 되는 것을 추구한다는 의미가 담겨 있을 것이다. 따라서 페어 트레이딩을, 방향성 투자보다 위험을 낮추고, 그 대신 기대수익률도 낮춘 투자 기법으로 이해할 필요가 있다.

[출처]25. 공적분 몬테카를로 시뮬레이션 (2)|작성자아마퀀트