[페어 트레이딩/고급편] 28. 단순회귀에 의한 헤지 비율 산출

페어 트레이딩 (Pairs Trading) – 추가편 (12)
단순회귀에 의한 헤지 비율 산출

그 동안 페어 트레이딩의 적정 헤지 비율을 결정하기위해서 공적분 계수나 회귀계수에 대해 언급해왔다. 이번 시간에는 회귀계수인 베타의 특징에 대해 자세히 살펴보기로 한다.

베타는 CAPM의 시장모형에서 도입되었고, 시장에 대한 상대적 수익률로 정의된다. 그리고 페어 트레이딩을 시장중립모형으로 만들기 위해 각 종목의 베타 비율을 헤지 비율, β(X) / β(Y), 로 사용하였다. β(X)와 β(Y)는 시장에 대한 상대적 개념 (β(M)에 대한 상대적 수익)이고, X, Y 간의 상대적 개념으로는 β(XY) 를 사용하였다 (종목 X에 대한 종목 Y의 상대적 수익). 페어 트레이딩에 β(XY)를 사용해도 무리가 없는지 확인해 보자.

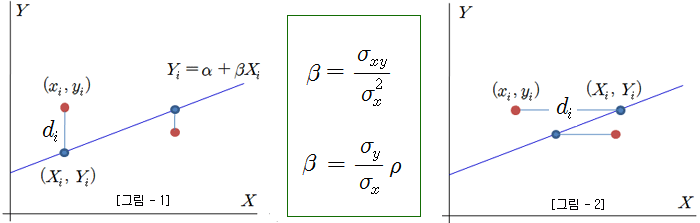
종목 X와 종목 Y의 상대적 베타는 위 그림과 같이 단순회귀직선에 의한 방법으로 계산할 수 있다. 이 모형은 상관관계가 있는 X와 Y의 관계식을 계산한 것이다. [그림-1]에서 빨간색 점은 실측치 (xi, yi)이고, 파란색 점 (Xi, Yi)은 이론적인 관계식 위에 위치한 점이다. 실측치와 이론치의 오차 (di)가 최소가 되도록 관계식의 모수 (α, β)를 추정한다.

그런데 이 모형은 X의 정보를 이용하여 Y를 추정하는 방식이다. 즉, X는 이미 알고 있는 값이고, Y는 불확실한 값으로 추정의 대상이다. X는 오차가 없고, Y만 오차가 있다. 따라서 오차인 di 는 Yi – yi 로만 표현된다 (Xi – xi = 0 임). 이 모형의 예로는 광고비 (X)와 매출액 (Y) 사이의 관계 같은 것을 들 수 있다. 광고비인 X 는 기업이 지출하는 항목으로 충분히 알 수 있는 값이지만, 매출액인 Y는 알 수 없으므로 추정이나 예측이 필요한 항목이다. 통계학적으로는 X를 독립변수, Y를 종속변수라 부르기도 하고, X를 설명변수, Y를 반응변수라고 부르기도 한다. 만약, 거꾸로 Y를 이용하여 X를 예측한다면 X 만 오차가 있을 것이고, 오차인 di 는 [그림-2]와 같이 된다. [그림-1]과 [그림-2]의 오차의 길이가 달라진다. 따라서 오차를 최소화하는 모수의 추정치가 달라진다 (α, β). 이 모형은 독립변수와 종속변수의 관계에 대해 적합한 모형이다.

그렇다면 페어 트레이딩의 두 종목은 독립변수와 종속변수의 관계인가? 그렇지 않다. 페어 트레이딩의 두 종목은 서로 대등한 위치에 있는 관계이고, 종목 X로 종목 Y를 설명할 수도 있고, 종목 Y로 종목 X를 설명할 수도 있다. 서로 대등한 관계이므로 X로 Y를 설명할 때와, Y로 X를 설명할 때의 베타는 역수의 관계가 성립해야 한다. 즉, 롱-숏 과 숏-롱의 헤지 비율은 서로 역수가 되어야 한다. 그런데, 단순회귀 모형을 사용하면 베타의 역수 관계가 성립하지 않는다. 위의 베타 수식을 보면 ρ = 1일 때 만 서로 역수의 관계가 성립한다. 따라서 단순회귀 모형에 의한 페어 트레이딩은 적합해 보이지 않는다.

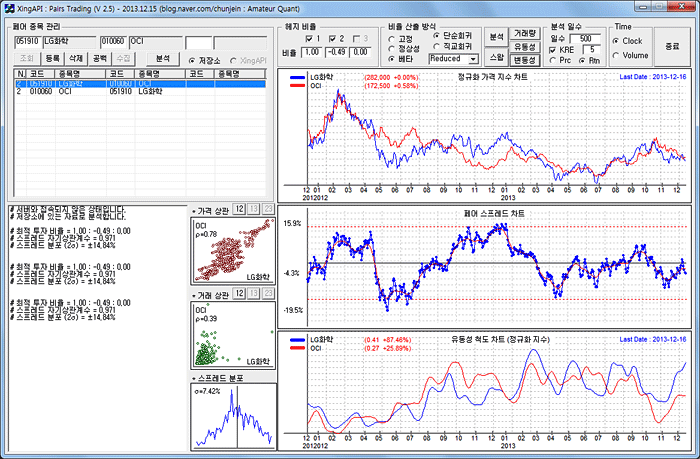
아래 그림은 LG화학과 OCI의 관계를 분석한 것이다. 단순회귀에 의해 베타를 계산하면 LG화학 : OCI = 1 : -0.49 가 나온다. 그리고 상관계수는 0.78 이다. 이것은 LG화학을 1단위 매수할 때 OCI를 0.49 단위를 매도하라는 의미이다 (상관계수와 베타는 수익률이 아닌 로그 주가를 이용하였음. 이 부분에 대해서는 나중에 …).

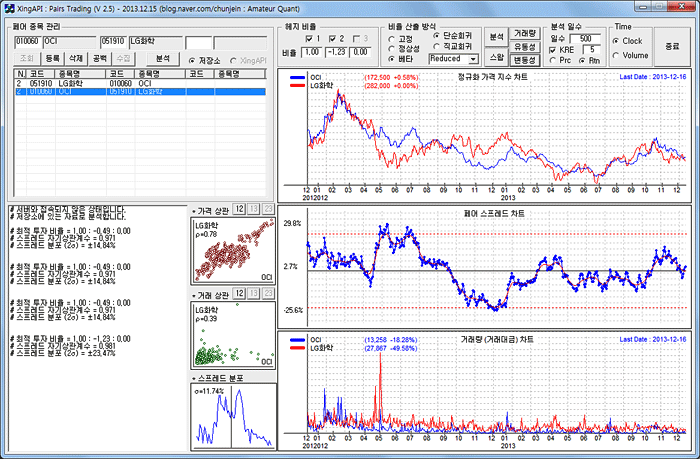
아래 그림은 순서를 바꿔서 베타를 계산한 결과이다. OCI : LG화학 = 1 : -1.23 이다. 이것은 OCI를 1 단위 매수할 때 LG화학을 1.23 단위 매도하라는 의미이다. 상식적으로 생각하면 OCI를 1단위 매수할 때 LG화학은 0.49의 역수인 2.04를 매도해야 할 것 같다.

회귀분석 모형이 페어 트레이딩에 적합하려면 X와 Y가 모두 불확실성 (Stochastic)을 갖는 변수이고, X, Y 모두 오차를 포함하고 있어야 한다 (dx = Xi – xi, dy = Yi – yi). 이런 형태의 모형을 직교회귀 분석(Orthogonal Regression) 이라 한다. 직교회귀에 대해서는 다음 시간에 자세히 알아보기로 한다.

단순회귀 모형의 β 산출 공식 유도 과정

단순회귀 모형에서 β는 아래 과정으로 계산할 수 있다. 원리는 오차의 제곱합이 최소가 되도록 회귀직선의 기울기를 결정하는 것이다. 아래 과정은 라그랑지 승수법 (Lagrange Multipliers)을 이용하였다. Y의 오차를 단순히 α, β로 미분하여 연립방정식을 풀면 쉽게 계산되지만, 다음 시간에 다룰 직교회귀 공식을 위해 약간 복잡한 과정을 거쳤다.

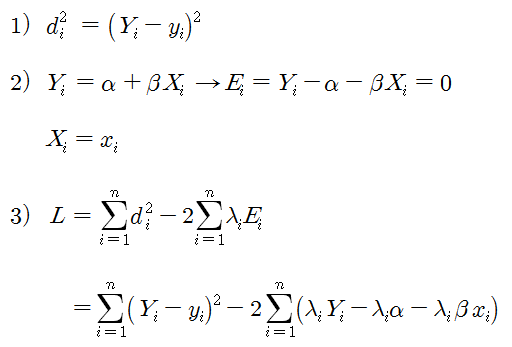
오차는 Y에만 존재하므로, 오차의 제곱합은 식 1)이 된다. 오차를 제곱하는 이유는 +, – 인 오차가 서로 상쇄되는 것을 방지하기 위함이다. 그리고 회귀직선은 식 2)가 된다. 여기서 실측치는 (xi, yi)이고, 이론치는 (Xi, Yi)이다. 식 1)은 목적함수 (Objective Function)가 되고, 식 2)는 제약함수 (Constraints)가 된다. 제약함수가 존재하는 목적함수를 최적화하기위해 라그랑지 승수법을 이용하면 식 3)이 된다.

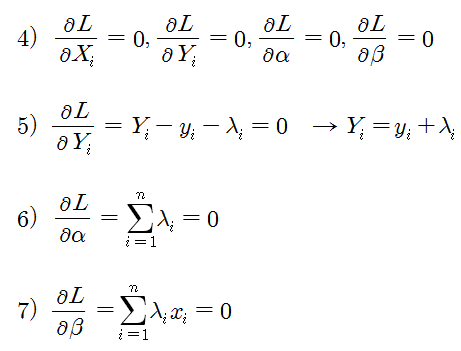
식 3)을 최적화 하기위해 추정 대상 변수들로 편미분하면 위와 같이 3개의 식을 얻을 수 있다, 식 5), 6), 7). 이 3개의 식을 이용하면 실측치인 xi, yi 로부터 β를 계산해 낼 수 있다.

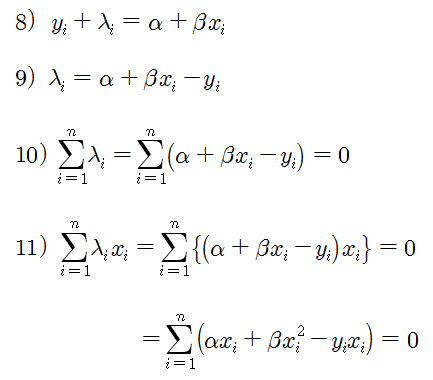
식 2)에 식 5)를 대입하면 식 8)이 되고, 라그랑지 승수 (λ) 들은 식 9)가 된다. λ를 식 6)과 7)에 대입하면 식 11) 이 된다.

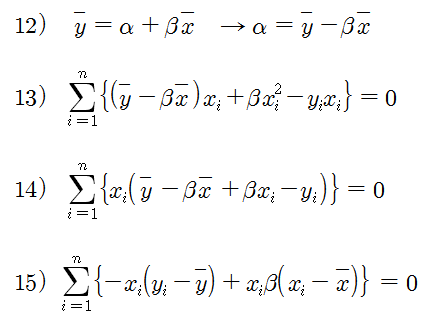
식 12)를 식 11)에 대입하여 α를 소거하면 식 13)이 되고, 이를 정리하면 식 15)가 된다

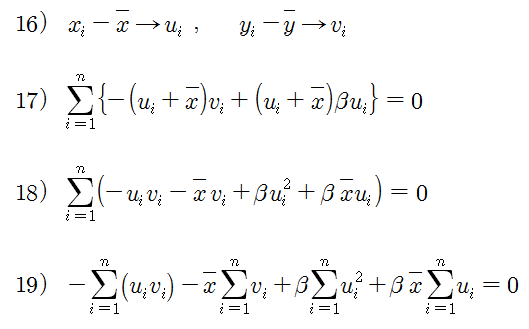
식 15)에서 xi, yi의 편차 값을 ui, vi로 치환하고 정리하면 식 19)를 얻을 수 있다. 여기서 xi, yi의 편차들의 합은 0 이므로 (식 – 20), 식 19)를 정리하면 식 21)을 얻을 수 있다.

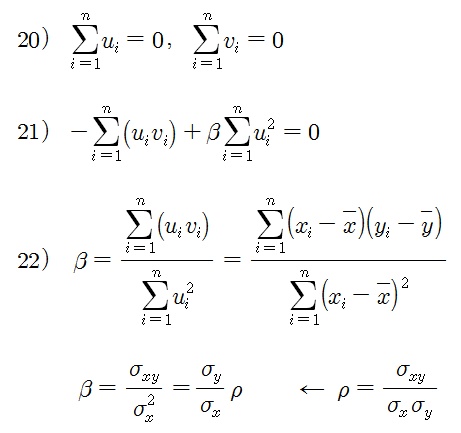
식 21)의 ui, vi를 다시 xi, yi의 편차 값으로 치환하면 최종적으로 식 22)를 얻을 수 있고, 이 식이 바로 단순회귀에 의한 베타의 계산식이다. 베타는 x와 y의 변동성 (표준편차)의 비율에 상관계수를 곱한 것으로 계산된다. ρ = 1 인 경우는 x로 y를 설명할 때의 β와 y로 x를 설명할 때의 β가 정확히 역수의 관계가 된다. 예를 들어, KODEX200 과 KODEX 레버리지의 변동성은 2배이고, 상관계수는 거의 1에 가깝다. 따라서 KODEX200을 1단위 매수할 때 KODEX레버리지는 0.5 단위 매도하면 헤지 관계가 성립한다. 반대로 KODEX레버리지를 1단위 매수할 때 KODEX200은 0.5의 역수인 2단위 매도해야 한다. ρ = 1인 경우는 포지션에 따라 베타의 역수 관계가 잘 성립한다. 그러나 대부분의 페어는 ρ < 1 이므로 베타의 역수 관계가 잘 성립하지 않는다.

이런 문제점을 해결하기 위해서는 직교회귀에 의한 베타를 생각해 볼 수 있다. 다음 시간에는 직교회귀에 대해 자세히 살펴보기로 한다.

[출처]28. 단순회귀에 의한 헤지 비율 산출|작성자아마퀀트