[페어 트레이딩/고급편] 30. 직교 (면적) 회귀에 의한 헤지 비율 산출

페어 트레이딩 (Pairs Trading) – 추가편 (14)
직교 (면적) 회귀에 의한 헤지 비율 산출

이전 시간에는 수직 거리가 최소가 되는 직교회귀에 대해 알아보았고, 페어 (Pair)가 상호 독립적 관계에 있을 때, 상대적 베타 값이 잘 설명된다는 것을 알아보았다. 그러나 이 방법은 베타의 수식이 너무 복잡해서 그 의미를 직관적으로 이해하기가 어렵다. 모형이나 수식이 복잡하고 정교하다고 해서 그 결과가 최선이라고 보기는 어려울 것이다. 오히려 단순하면서도 상식에 잘 부합하는 것이 의사결정에 도움이 되는 경우가 많다.

이번 시간에는 아래 그림과 같이 수직 거리를 대각선으로 사각형의 면적을 최소로 만드는 베타 값에 대해 살펴보기로 한다. 수직 거리나 면적은 X, Y를 바꾸어도 변하지 않는다. 즉, X, Y가 상호 독립인 경우에 해당하고, 베타 값은 서로 역수 관계에 있다.

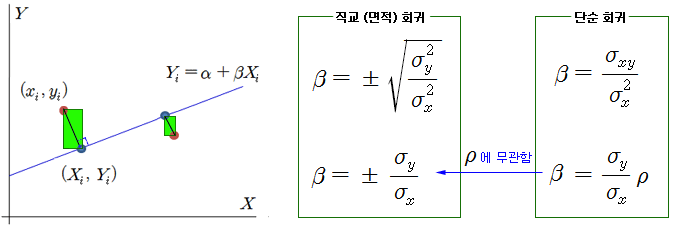
이 방법으로 베타를 계산하면 위 그림과 같이 아주 간단하게 나온다. 베타는 두 종목의 변동성의 비율과 같아진다. 단순회귀에서 상관계수가 1일 때의 베타 값과 일치한다. 이 결과는 상식에 잘 부합한다. 공적분이나 회귀분석을 전혀 몰라도 두 종목간의 헤지 비율을 구하려면 누구나 변동성 비율을 계산할 것이다. 변동성이 높은 종목은 조금만 매수 (매도)하고, 변동성이 낮은 종목은 많이 매도 (매수)해야 헤지 관계가 잘 성립한다.

위의 수식을 직관적으로 이해하면 다음과 같다. 단순회귀에서 X로 Y를 설명할 때의 베타 (βxy)와 Y로 X를 설명할 때의 베타 (βyx)가 있을 때, 상관계수가 높다면 βxy 와 βyx의 역수는 유사할 것이다. 두 계수 (βxy 와 βyx의 역수)의 기하평균을 계산해 보면 아래와 같고, 결과는 위의 식과 동일하다. 즉, 오차의 면적이 최소가 되는 베타 계수는 단순회귀의 베타 계수들 간의 기하평균이 된다 (Geometric Mean Regression, GMR). 이 때 각 오차 (Xi – xi 와 Yi – yi) 분포의 분산은 같아야 한다. 만약 어느 한 쪽이 더 크다면 독립과 종속의 성분이 포함된다.

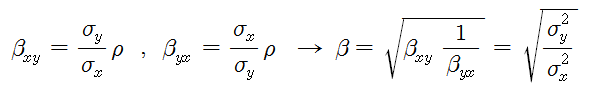
아래 그림은 이전 포스트처럼 LG화학과 OCI의 관계를 분석한 것이다. 베타 계산 결과는 LG화학 : OCI = 1 : -0.63 으로 단순회귀나 직교 (거리) 회귀보다 약간 높게 나온다. 두 종목을 역으로 계산하면 LG화학 : OCI = 1 : -1.58로 역수 관계가 잘 성립한다 (1/0.63 = 1.58).

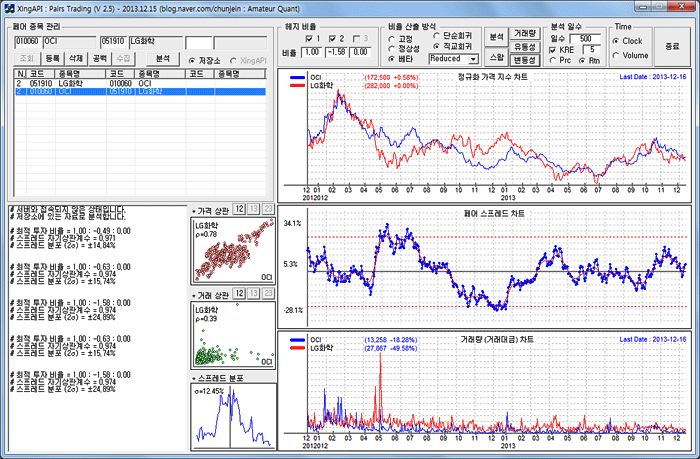
직교 (면적) 회귀 모형의 β 공식 유도 과정

이 방법도 이전 방법과 동일하게 라그랑지 승수법 (Lagrange Multipliers)을 이용하면 된다. 식 1)의 목적 함수만 면적으로 바꾸면 된다. 식 1)로 표현된 목적 함수는 위 그림의 면적을 의미하고, 항상 양수가 되므로 이 식을 최소로 만드는 베타 값을 구하면 된다.

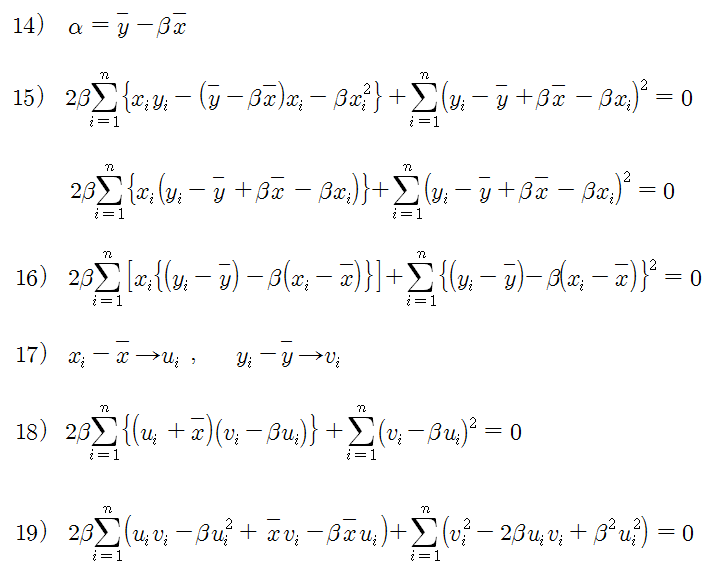
이번 시간에는 최소 면적에 의한 직교회귀에 대해 알아보았고, 수직 거리에 의한 직교회귀보다 간단하면서도 직관적으로 상식에 잘 부합된다는 것을 알았다.

그 동안 헤지 비율을 결정하기위해 공적분 계수, 단순회귀, 직교 (거리) 회귀, 직교 (면적) 회귀에 대해 알아보았다. 그런데 각각의 문제점을 보완하다보니 여러 개의 헤지 비율이 등장했고, 이 중 어느 것을 사용하는 것이 좋을지에 대한 의문이 생기게 된다. 다음 시간에는 페어의 특성에 따라 어느 것을 사용하는 것이 좋은지에 대해 살펴보기로 한다.

[출처]30. 직교 (면적) 회귀에 의한 헤지 비율 산출|작성자아마퀀트