News & Events
[페어 트레이딩/고급편] 34. Partial Correlation을 이용한 페어 트레이딩
페어 트레이딩 (Pairs Trading) – 추가편 (18)
Partial Correlation을 이용한 페어 트레이딩
페어를 선정할 때 두 종목의 상관성을 분석해 보니 상관관계가 높은 것으로 관측되었다. 그런데 이 상관성이 두 종목의 실제 관계라 할 수 있는가? 아니면 다른 어떤 요인에 의해 그렇게 보이는 건 아닌가?
위 질문에 대한 답은 Partial Correlation (편상관관계)에서 찾을 수 있다. 예를 들어 보자. 어느 나라든 교회수와 범죄수의 상관관계를 측정해 보면 (+) 상관관계가 있는 것으로 측정된다고 한다 (다른 종교단체, 학교 등도 동일할 것임). 그런데 상식적으로는 (-) 상관관계가 더 어울릴 것으로 보인다.
교회수나 범죄수는 인구가 증가할수록 증가한다. 즉, 교회수나 범죄수는 인구 증가와 (+) 상관관계가 있다. 만약, 인구 증가의 효과를 빼고 둘 간의 상관관계를 측정해 보면 그래도 (+) 상관관계가 있는가? 그렇지 않다고 한다. 인구 증가 효과를 제거하고 교회수와 범죄수의 상관관계를 측정해 보면 실제로는 (-) 상관관계가 나온다고 한다. 이렇게 측정한 것이 Partial Correlation의 개념이다.
위의 논리를 페어 트레이딩에 그대로 적용해 보면 아래와 같다. 종목-1 과 종목-2 가 밀접한 상관관계가 있는 것으로 관측되었더라도 시장의 효과를 제거한 후 두 종목의 상관성을 관찰해 볼 필요가 있다. 실제로는 두 종목에 상관성이 없음에도 불구하고 시장이 올랐기 때문에 두 종목이 같이 오를 수도 있기 때문이다. 여기서 시장 효과는 종합주가지수로 생각해 볼 수 있다.
두 종목에서 시장 효과를 제거하는 방법의 수학적 표현은 아래와 같다. 식 (1)은 Z가 주어진 상태에서, Z의 영향을 뺀 X와 Y의 상관계수이고, 이것이 Partial Correlation의 표현이다. 식 (1)에서 Z의 영향을 제거하는 방법으로는 회귀분석을 생각해 볼 수 있다. 식 (2)는 단순 선형회귀로 X와 Y를 Z로 최대한 설명해 보려는 식이다. 여기서 Z로 최대한 설명하고 남은 잔차 성분이 바로 Z의 영향을 제거한 X와 Y이고, 식 (3)은 두 잔차성분 간의 상관계수이다. 이 식이 Partial Correlation을 계산하는 표현식이다. 참고로 식 (4)는 식 (3)으로부터 얻을 수 있는 관계식이다.
위의 식이 의미하는 바를 페어 트레이딩에 적용해 보자. 아래 예는 2009년도 삼성전자와 SK하이닉스 페어를 분석한 결과이다. 이 시기는 금융위기 직후로 거의 모든 주가가 동반 상승한 때였다. 삼성전자와 SK하이닉스의 (로그 가격) 상관계수는 0.957로 매우 높게 측정되었다. 그런데 이 관계가 실제 둘의 관계인지, 아니면 종합이 올랐기 때문에 덩달아 오른 것인지는 확실치 않다. 실제로 삼성전자와 종합의 상관계수는 0.952 였고, SK하이닉스와 종합의 상관계수는 0.960 이었다.
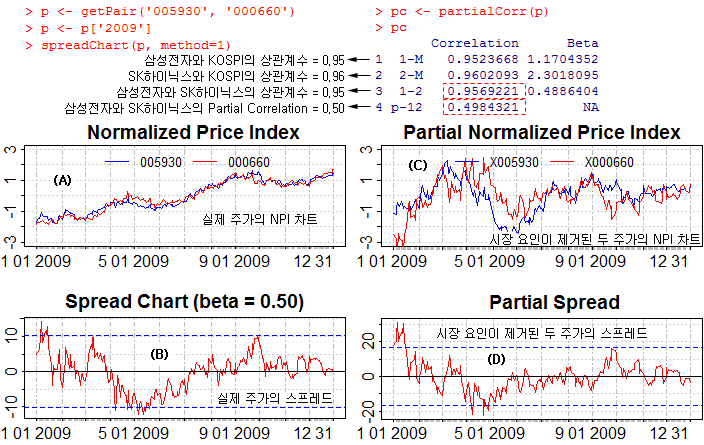
이 페어의 NPI 차트는 그림 (A)와 같다. 두 주가가 매우 유사하게 움직이는 것으로 보인다. 그리고 둘 간의 스프레드는 그림 (B)와 같다. 스프레드가 -10% ~ +10% 범위안에서 비교적 안정적으로 움직이고 있다 (그림의 R 명령은 필자가 만들어 본 R-함수인데, 개념을 설명하는데는 별로 중요치 않으므로 설명은 생략하기로 함).
둘 간의 Partial Correlation을 생각해 보자. 여기서는 위의 수학식을 그대로 사용하지 않고 페어 트레이딩의 스프레드 개념으로 접근해 보았다. 삼성전자와 종합주가지수를 하나의 페어로 스프레드-1 (X005930) 을 계산해 보고 (단순 회귀분석에 의해), SK하이닉스와 종합주가지수를 하나의 페어로 스프레드-2 (X000660) 를 계산해 본다. 그러면 스프레드-1 은 삼성전자에서 종합주가지수의 효과를 뺀 주가의 움직임이 되고, 스프레드-2 는 SK하이닉스에서 종합주가지수의 효과를 뺀 주가의 움직임이다.
두 종목에서 모두 종합주가지수의 효과가 제거되었으므로, 스프레드-1과 스프레드-2의 상관관계를 분석하면 이것이 바로 Partial Correlation이 된다. 실제 계산해 보면 둘 간의 Partial Correlation은 0.499 가 나온다. 원래 상관계수인 0.957 보다 반 정도가 줄어든다.
스프레드-1과 스프레드-2를 하나의 페어로 생각해 보면 둘 간의 관계는 그림 (C)와 (D)가 된다. Partial NPI는 그림 (A)보다 괴리가 더 존재하고, Partial Spread는 -20% ~ +20% 범위에서 움직이므로 그림 (B)보다 더 큰 폭으로 움직인다.
Partial Spread도 어느 정도 정상성이 있어 보이므로 페어 트레이딩의 대상이 될 수 있다. Partial Spread로 페어 트레디딩을 하려면 종합주가지수 효과가 개입되었으므로 종합도 포지션에 포함시켜야 한다 (선물, ETF 등으로). 즉, 삼성전자 매수 – SK하이닉스 매도 – 종합 매수 (or 매도) 와 같이 3-자 페어 트레이딩과 유사하게 된다. 종합을 얼마만큼 매수 혹은 매도할 것인지는 각 종목과 종합에 대해 회귀분석할 때 결정되는, 식 2에서 결정된, α 와 β에 의해 결정한다.
실제 시장에서 페어를 선정할 때 Partial Correlation을 고려해야 하는 페어가 많지는 않겠지만 Partial 관계가 존재하는지 체크해 볼 필요는 있다.
