[페어 트레이딩/고급편] 35. 페어 트레이딩의 표준 절차

페어 트레이딩 (Pairs Trading) – 추가편 (19)

페어 트레이딩의 표준 절차

페어 트레이딩을 설계할 때 고려해야할 사항들은 대단히 많다. 다른 투자 전략과 마찬가지로 정답이 없는 불확실성의 세계에서 최적의 방안을 찾아야하기 때문이다. 성공적인 페어 트레이딩을 위해서는 각 종목에 대한 Fundamental Analysis도 필요하고, 통계적인 기술적 분석도 필요하다. Fundamental Analysis는 매우 주관적이고 투자자의 효용 (Utility)에 따라 분석 결과가 다를 수 있다 (이질적 기대감). 반면에 통계적인 기술적 분석은 이 보다는 객관적이라 할 수 있다. 물론 통계적 분석도 기준이나 기간 설정이 투자자마다 다를 수 있으므로 분석 결과도 다를 수 있다.

모든 전략은 분석의 표준 (기준)이 필요하다. 설령 그 표준에 오류가 있더라도 없는 것 보다는 낫다. 필자가 생각하는 통계적인 기술적 분석에 대한 표준을 아래와 같이 정리해 보았다.

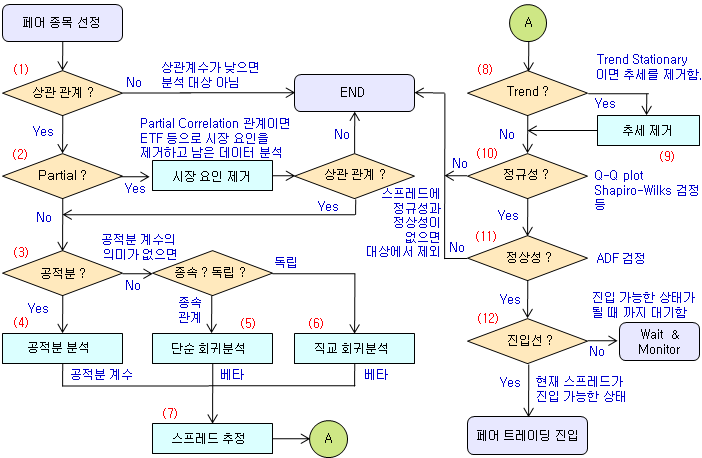
(1) 페어 트레이딩 대상에 상관성이 있는지 확인한다. 상관성이 전혀 없으면 분석 대상에서 제외한다. 상관성은 상관계수로 측정할 수 있다. 상관계수는 가격과 수익률로 각각을 측정할 수 있으며, 두 상관성이 일치하지는 않는다. 수익률 상관계수가 높아도 가격 괴리가 점점 커진다면 가격 상관계수는 낮을 수도 있다. 페어 트레이딩을 위해서는 로그 가격의 상관계수가 큰 것을 선택한다.

(2) Partial Correlation 관계가 있는지 확인한다. 단계 (1)에서 상관성이 있더라도, 시장 요인 때문에 상관성이 높게 측정되었던 건 아닌지 확인한다. 확인 방법은 시장 요인을 제거하고 남은 잔차 성분들에 상관성이 있는지 확인하면 된다. 두 잔차에 상관성이 없으면, 두 종목 간에 실제적인 상관성이 없는 것이므로 페어 트레이딩 대상에서 제외한다. 시장은 종합주가지수를 대용치로 사용할 수 있고, 시장 요인은 회귀분석으로 제거한다.

(3) 페어에 공적분 (Cointegration) 관계가 있는지 확인한다. 우선 공적분 분석을 시도해서 공적분 계수를 추정해 본다. 공적분 계수 추정은 여러 방법이 있을 수 있다. 회귀분석에 의한 베타 값도 공적분 계수가 될 수 있다. 여기서는 스프레드의 정상성을 중시하여 ADF 검정의 p-value를 최소로 만드는 계수를 공적분 계수로 사용하기로 한다. 공적분 계수가 상식적인 수준이면 공적분 분석 단계로 간다. 추정된 공적분 계수가 이상한 값이 나올 수도 있다. 만약, 종목-1을 기준으로 종목-2에 대한 공적분 계수가 0 에 가까운 값이 나온다면, 종목-1을 1 단위 매수할 때, 종목-2는 0 단위 매도하라는 의미이므로, 롱-숏이 아닌 방향성 투자가 된다. 즉, 페어 트레이딩의 대상이 아닌 게 된다. 이런 원인은 종목-1의 주가가 이미 최대 정상성을 가졌기 때문이다 (종목-1이 등락만 반복하여 횡보하는). 이런 경우는 회귀분석 단계로 넘어간다.

(4) 단계 (3)에서 추정한 공적분 계수로 스프레드를 추정한다. 참고로, 공적분 계수 추정시 스프레드가 AR(1) 모형을 따른다고 가정하여 스프레드의 자기상관계수 (시차=1)가 최소가 되는 계수를 사용해도 무방하다. 또한, ADF 검정은 결정적 추세가 있는 정상 시계열 (Trend Stationary)도 정상성이 있는 것으로 판단하지만, 여기서는 추세 없이 정상성만을 최대로 만드는 계수를 사용하기로 한다.

(5) 공적분 분석이 용이하지 않으면 회귀분석에 의해 베타 계수를 추정한다. 두 종목 간에 종속성이 있으면 단순 회귀분석으로 베타를 추정한다. 이런 경우는 지수와 종목, 지주사와 계열사, 보통주와 우선주 등이 있다.

(6) 두 종목이 종속성이 없는 독립적인 관계라면 직교 회귀분석에 의해 베타를 추정한다. 두 종목에 상관성이 없으면 베타값 추정이 곤란하지만, 상관성이 없는 경우는 이미 단계 (1)에서 제외되었으므로 문제될 것은 없다.

(7) 추정된 공적분 계수 혹은 베타를 이용해서 스프레드를 추정한다. 스프레드 계산은 로그 가격을 기준으로 계산한다 (log regression). 로그 가격을 사용하는 이유는 스프레드가 수익률 개념이 되어 기대 수익률 예측이 용이하고, 스프레드의 통계적 분포 특성도 좋아지기 때문이다.

(8) 추정된 스프레드에 추세가 존재하는지 확인한다. 공적분 분석에 의한 스프레드에는 추세가 없겠지만 (단계 (4)에서 제거되었음), 회귀분석에 의한 스프레드에는 추세가 있을 수 있다.

(9) 스프레드에 추세가 존재하면 추세선을 균형선으로 사용해야 한다. 즉, 스프레드가 추세선에서 멀어지면 두 주가는 괴리가 발생하는 것이고, 추세선으로 회귀하면 두 주가는 균형점으로 오는 것이다. 그런데 이 추세가 결정적 추세일지 확률적 추세일지를 판단해야 한다. 사실 어떤 추세인지 판단하기는 매우 어렵다. 주관적인 판단으로 결정적 추세로 생각되면 (Fundamental Analysis에 의해 스프레드의 추세를 인정할 수 있으면), 추세를 제거하고 남은 잔차의 정상성이 존재하는지 확인한다. 정상성이 높다면 페어 트레이딩의 대상이 될 수 있다. 추세를 제거하는 방법은 회귀분석을 이용한다.

(10) 스프레드의 정규성 (Normality) 검정을 수행한다. 정상적인 스프레드라면 균형점 부근에서 많은 점들이 관측되고, 균형점을 벗어난 지점에서는 조금만 관측되어야 한다. 두 주가가 대부분 균형점 근처에 있다가 가끔씩 균형점에서 벗어났다가 회귀하는 모습이 안정적으로 보이기 때문이다. 이 특성은 스프레드의 분포가 정규분포에 가까운지 아닌지를 확인하면 된다. 통계적인 방법으로는 Q-Q plot을 그려보는 방법이나, Shapiro-Wilks 등으로 정규성을 검정해 보는 방법이 있다. 정규성이 없으면 대상에서 제외한다.

(11) 스프레드의 정상성 (Stationality) 검정을 수행한다. 스프레드를 추정할 때 이미 고려된 사항이지만, 최종적으로 스프레드의 정상성을 체크한다. 육안으로 확인하는 것도 휼륭한 방법이다. 통계적 방법으로는 ADF 검정 등이 있다. ADF 검정의 p-value가 충분히 작으면 정상성이 있는 것으로 판단한다.

(12) 스프레드의 현재 시점이 진입선을 벗어난 상태인지 균형점 근처에 있는 상태인지 확인한다. 진입선을 벗어난 경우라면 페어 트레이딩을 수행하고, 균형점 부근이라면 관찰 대상으로 분류하고 진입선을 벗어나는지 지속적으로 모니터링 한다. 투자자의 성향에 따라 진입선을 벗어날 때 분할 매수로 진입할 수도 있고, 진입선을 벗어났다가 다시 진입선 안으로 들어올 때 진입할 수도 있다.

이상으로 필자가 생각하는 페어 트레이딩의 표준 절차를 정리해 보았다. 위에서 언급한데로, 불확실성 세계에서 모든 투자자가 동의하는 절대적 표준은 있을 수 없다. 이 절차를 기본으로 자신의 목적에 맞는, 자신만의 표준 절차를 수립할 때 참조용으로 활용할 수는 있을 것이다.

[출처]35. 페어 트레이딩의 표준 절차|작성자아마퀀트