[페어 트레이딩/고급편] 4. 페어트레이딩의 위험 측정

페어트레이딩 (Pairs Trading) – 고급(4)

페어트레이딩의 위험 측정

위험 자산의 위험의 정도는 수익률의 분산으로 측정한다 (혹은 표준편차). 즉, 수익률의 변동이 심한 정도를 위험으로 나타내는 것이다. 수익률의 변동이 크면 위험이 큰 것이고, 변동이 작으면 위험이 작은 것이다. 이 방법은 1953년 마코비츠가 “포트폴리오 선택 이론”에서 제시한 것으로 지금까지도 널리 사용되고 있다. 실무에서는 최대 손실 가능성을 금액으로 표시한 VaR (Value at Risk)라는 척도가 사용되기도 하지만, 이론을 전개할 때는 일반적으로 분산을 사용한다. 페어트레이딩도 페어를 롱/숏 포트폴리오로 구성한 것이므로 포트폴리오 이론에서 제시한 대로 분산을 사용해서 위험을 측정하면 무난할 것이다.

포트폴리오의 위험 측정

두 종목으로 구성된 포트폴리오의 수익률과 위험 (분산)은 아래 식으로 측정한다. 포트폴리오의 수익률(rp)은 두 종목의 가중 평균 수익률로 나타내고 (식 1), 위험은 수익률의 분산을 계산한 것이다 (식 2).

1) 식은 종목-1을 w1(%)의 비율로 매수하고, 종목-2를 w2(%)의 비율로 매수했을 때 포트폴리오의 수익률이다. 두 종목 모두 매수 포지션이므로 w1 + w2 = 100%가 된다. 만약 한 종목은 매도했을 때의 포트폴리오라면, 차입 매도로 초기 비용이 발생하지 않으므로, w1 + w2 > 100% 가 된다. 즉 종목-1을 100% 매수하고 그 만큼 종목-2를 매도했다면 w1 + w2 = 200%가 된다.

2) 식은 1) 식의 분산을 계산한 식이다. 만약 두 종목이 완전히 동일하게 움직이면 (r1 = r2 이면) 완전상관이 되어 포트폴리오의 분산은 각 종목의 가중평균 분산이 된다 (위험감소효과 없음). 그러나 대부분의 경우 상관계수는 1보다 작으므로 포트폴리오의 분산은 각 종목의 분산을 가중 평균한 값보다 작아진다. 이것을 위험감소효과 또는 분산투자효과라고 한다.

페어트레이딩의 위험 측정

페어트레이딩의 위험도 위의 방법과 동일하게 측정한다. 단, 롱/숏으로 매도 포지션이 포함되므로 이 부분만 고려하면 된다. 식으로 표현하면 아래와 같다.

3) 식은 페어 포트폴리오의 수익률이다. 종목-2가 매도 포지션이므로 종목-2의 수익률은 빼주어야 한다.

가중치는 종목-1을 100%로 하고, 종목-2는 헤지 비율(n : Cointegration 계수) 만큼의 차입 매도이므로 초기 비용이 들어가지 않는다. 따라서 가중치의 합은 100%보다 크다 (헤지 비율이 1이라면 가중치의 합은 200%가 되므로 레버리지 효과가 발생한다).

매도 포지션은 수익률이 반대인 자산 (즉 -r2)을 매수한 것으로 생각하여, 식 2)의 r2 대신에 -r2를 대입하면 된다. 그러면 페어 포트폴리오의 분산은 식 4)와 같이 되고, 정리하면 식 5)와 같이 된다. r1과 r2가 같은 방향이고 r2가 매도이므로 분산에서 공분산이 차감되는 것이다.

또한 페어 포트폴리오의 수익률은 스프레드의 차이므로, 식 6)과 같이 포트폴리오의 수익률 분산은 스프레드의 차에 대한 (차분 스프레드) 분산과 같다.

결과를 확인하기 위해 삼성중공업과 대우조선해양을 페어로 묶어 실제 계산을 해 보았다. 데이터는 종가 기준으로 600개로 하였다.

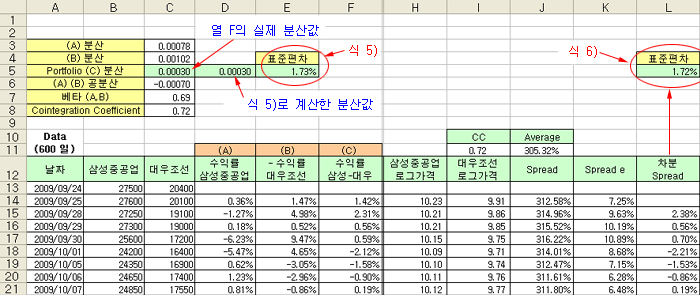
열 (A~F)는 두 종목의 실제 수익률을 구해서 표준편차를 구한 값이고, 열 (H~L)은 페어트레이딩으로 계산한 스프레드로 구한 표준편차이다. 열(F)의 실제 합성 수익률에 대한 분산과 (0.00030), 식 5)로 계산한 분산이 (0.00030) 잘 일치한다. 또한, 식 5)로 계산한 수익률 표준편차와 (1.73%), 식 6)으로 계산한 차분 스프레드의 표준편차가 (1.72%) 잘 일치한다.

결론적으로 삼성중공업과 대우조선해양의 위험은 차분 스프레드의 표준편차로 나타낼 수 있으며 그 값은 1.72% 이다. 이 값은 스프레드가 하루에 평균적으로 1.72% 변동하는 것으로 해석한다. 이 수치가 커지면 위험이 높은 것이고, 작으면 위험이 낮아지는 것이다.

만약 r1과 r2가 비슷하다면, 식 5)는 아래와 같이 식 7)로 표현할 수 있다. 즉, 가격의 변동이 비슷하면 Cointegration 계수가 1이 되어 식 7)은 0 이 된다. 즉 위험이 완전히 상쇄되는 것이다. 이것은 r1과 r2가 비슷하면서 매도로 인해 방향이 반대이므로 위험이 상쇄되는 결론과 잘 부합한다. 역으로 생각하면 Cointegration 계수가 1에 가까울수록 위험이 작다는 것을 알 수 있다. 기초편에서 보통주와 우선주의 Cointegration 계수가 1에 가까워 위험이 작다는 언급과도 잘 부합한다.

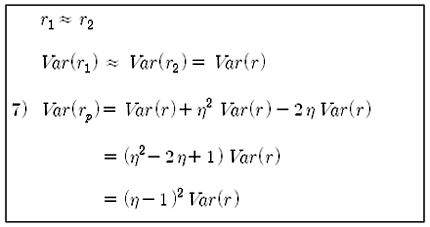
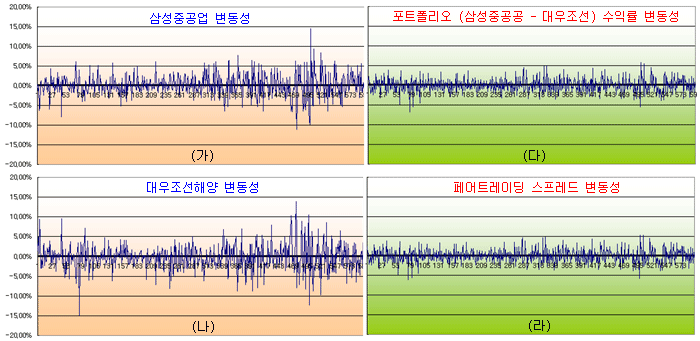
이번에는 위의 결과를 그림으로 확인해 보자. 아래 그림의 (가)와 (나)는 개별 종목의 수익률 변동성이고, (다)는 두 종목의 합성 수익률에 대한 변동성이다 (포트폴리오의 변동성). (라)는 페어 포트폴리오의 스프레드 변동성이다. (다)와 (라) 모두 개별 종목에 비해 변동성이 상당히 줄어든 것을 볼 수 있다.

샤프 비율 (Sharp Ratio)

샤프 비율은 위험 1단위당의 수익률로, 수익률을 위험으로 나눈 값이다. 위험이 작고 수익률이 높으면 샤프 비율은 높아진다. 샤프 비율은 실현 수익률을 이용하여 펀드의 성과를 평가하는데 사용되지만, 기대 수익률을 사용하면 향후 투자 대상에 대한 지표로도 사용할 수 있다.

페어트레이딩의 수익률은 스프레드의 차이고, 위험은 차분 스프레드의 표준편차이다. 따라서 페어트레이딩의 샤프 비율은 스프레드의 차를 차분 스프레드의 표준편차로 나눈 값이다. 투자 대상으로 여러 페어가 선정되었다면, 각 페어의 샤프 비율을 계산하여, 샤프 비율이 높은 페어를 선정하면 페어트레이딩의 효율을 더 높일 수 있다.

예를 들어보자. 아래 그림과 같이 페어-A의 현재 스프레드가 -9.50%이고, 균형점까지 올라가는 것을 목표로 한다면 기대 수익률은 +9.50%가 된다. 페어-B의 기대 수익률도 마찬가지로 하면 +12.00%가 된다. 페어-B의 기대 수익률이 페어-A보다 높지만 위험도 크므로 (2.50%), 페어-B가 꼭 유리하다고 할 수는 없다. 샤프 비율을 계산해 보면 페어-A가 5.52로 페어-B의 4.80 보다 높으므로 페어-A가 더 유리하다. 즉, 페어-A의 위험 한 단위당 수익률이 페어-B 보다 더 높은 것이다.

이상으로 페어트레이딩의 위험을 측정하는 방법에 대해 살펴보았다. 간단히 요약해 보면 아래와 같다.

1. 페어트레이딩의 기대 수익률은 스프레드의 차이다. (기초편에서 이미 언급한 내용임)

2. 페어트레이딩의 위험은 차분 스프레드의 표준편차로 측정한다.

3. Cointegration 계수가 1에 가까울수록 위험이 줄어든다.

4. 측정한 위험으로 샤프 비율을 활용하면 페어트레이딩의 효율을 높일 수 있다.

[출처]4. 페어트레이딩의 위험 측정|작성자아마퀀트