News & Events
페어트레이딩 (Pairs Trading) – 고급(7)
스프레드의 정규성 검정 이전 포스트에서는 스프레드의 히스토그램을 그려서 정규분포와 모양이 유사한지를 육안으로 비교해 보았다. 이번 시간에는 육안으로 비교하는 것이 아니라 통계적 기법을 이용하여 비교해 보자. 육안 비교만으로도 충분하지만, 한 번 정도 과학적인 검증을 해 봤다는데 의미를 두면 될 것 같다.
이전 포스트에서 삼성전자 우선주와 보통주의 600일 간 데이터를 이용하여 스프레드 도수를 구해 보았다. 이 차트에 아래와 같이 표준편차, 구간 확률, 기대 도수, 도수 잔차 제곱을 추가로 계산한다. 그리고 정규성 검정을 위해 유의 수준은 5%로 정하고, 자유도와 유의 확률을 계산한다.
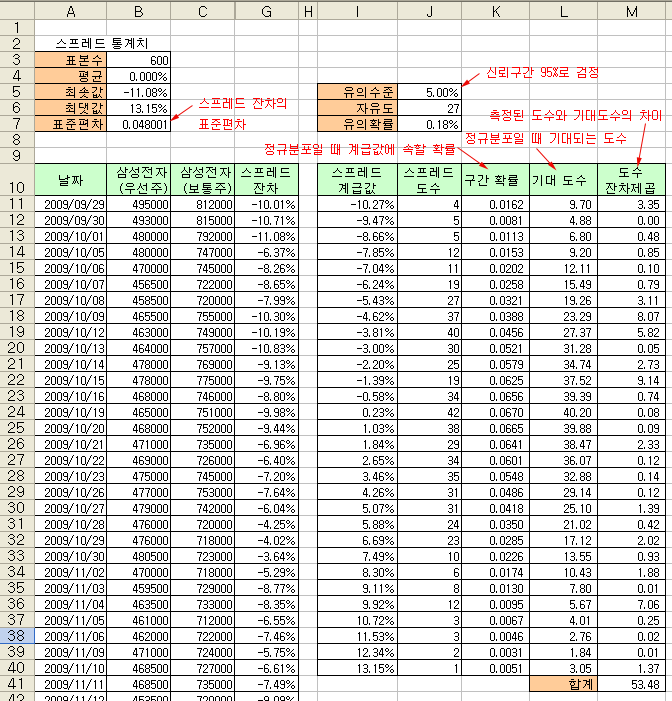
* 표준편차 셀(B7) = STDEV(G11:G610)
구간 확률 : 스프레드 계급값이 정규분포 상에 분포할 확률
셀(K11) = NORMDIST(I11,$B$4,$B$7,1)
셀(K12) = NORMDIST(I12,$B$4,$B$7,1)-NORMDIST(I11,$B$4,$B$7,1)
셀(K13) = NORMDIST(I13,$B$4,$B$7,1)-NORMDIST(I12,$B$4,$B$7,1)
.
.
셀(40) = 1-NORMDIST(I39,$B$4,$B$7,1)
기대 도수 : 정규분포 상에서 예상되는 도수
셀(L11) = $B$3*K11
셀(L12) = $B$3*K12
.
.
도수 잔차 제곱 : 관측된 도수와 기대 도수와의 상대적 차의 제곱
셀(M11) = ((J11-L11)^2)/L11
셀(M12) = ((J12-L12)^2)/L12
.
.
도수 잔차제곱의 합 셀(M41) = SUM(M11:M40)
자유도 = 구간수 – 2 – 1 = 27
위와 같이 각 셀을 계산한 후 관측된 스프레드 도수와 정규분포 상의 기대 도수를 그려 보면 아래 그림의 오른쪽과 같이 된다. 표본으로부터 관측된 스프레드 도수가 정규분포와 비교하여, 삼성전자 우선주와 보통주의 스프레드 모집단이 정규분포라고 말할 수 있는지를 검증하는 것이다. 두 도수 간의 차가 작을수록 두 집단은 같은 것이 된다. 그러므로 두 도수 간의 차이가 통계적으로 유의한지를 판단하면 된다. 그림에서 보면 정규분포 왼쪽 부분에서 스프레드 도수가 많이 벗어나 있는 것을 볼 수 있다. 통계학적인 결론은 “유의 확률 (p-value)이 0.18%로 유의수준인 5% 보다 작으므로 정규분포라고 할 수 없다.” 이다.
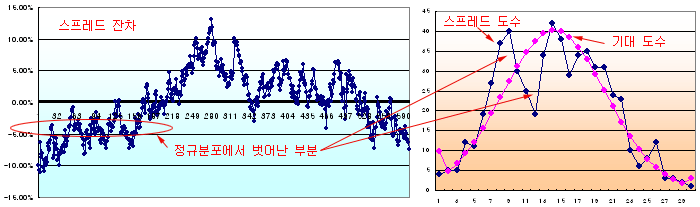
정규분포에서 많이 벗어난 부분의 스프레드 계급값은 -3.00% ~ -3.81% 구간과, -1.39% 구간이다. 왼쪽 스프레드 차트에서 보면 대략 2009.9 ~ 2010.1 사이에 우선주가 저평가 상태로 있었기 때문인 것으로 보인다.
스프레드의 특성은 분석 기간에 따라 달라진다. 위의 예에서는 600일 간의 데이터로 분석한 결과이나, 300일 간 데이터를 사용하면 유의 확률이 26.59%로 유의 수준보다 높으므로 아래와 같이 정규분포가 된다. 300일 간의 표본도 1년 2개월 정도의 데이터이므로 그렇게 작은 것은 아니다. 그러므로 삼성전자 우선주와 보통주의 스프레드는 정규성을 만족한다고 보아도 크게 무리가 없어 보인다.
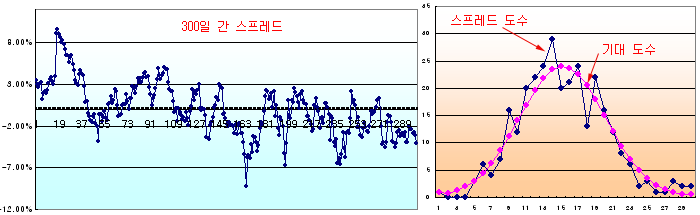
결론적으로 삼성전자 우선주와 보통주의 경우 600일 간 (약 2년 반)의 스프레드는 정규성을 만족하지 못하지만, 최근 300일 간 (약 1년 2개월)의 스프레드는 정규성을 만족한다는 것을 알았다. 우선주의 경우 스프레드는 보통주와의 주가 비율인 괴리율과 의미가 같다. 그러므로 “장기적인 괴리율에는 정규성이 없지만 단기적인 괴리율에는 정규성이 있다.” 라고 말 할 수 있다.
이상으로 스프레드의 정규성 검정에 대해 알아보았다. 페어트레이딩에는 장기적이나 단기적이나 모두 정규성을 만족하는 페어가 당연히 좋을 것이다. 그러나 단기적인 특성이 좋다면 페어트레이딩을 하는 데 큰 무리는 없어 보인다. 만약 거꾸로 장기적인 특성은 좋으나 단기적인 특성이 좋지 않다면, 단기적인 위험이 존재하고, 스프레드가 수렴하는데 시간이 많이 걸릴 가능성이 있으므로 적합하지 않을 수도 있다.
[출처]7. 스프레드의 정규성 검정|작성자아마퀀트


