[페어 트레이딩/기초편] 17. 공적분 계수 추정 방법

페어트레이딩 (Pairs Trading) – 추가편(1)

공적분 계수 추정 방법

페어트레이딩에 대해 오랜만에 글을 써 보는 것 같다. 그 동안 Market Microstructure 등 다른 분야에 몰두하다 보니 페어트레이딩에 대해서는 시간을 많이 할애하지 못했지만 페어트레이딩 분야에서 매듭짓지 못한 부분이 있어, 기초편-고급편에 이어 추가편에 기록해 보기로 한다.

추가편에서는 공적분 계수 (Cointegration Coefficient)에 대한 실질적인 추정방법에 대해 알아보기로 한다. 기초편과 고급편에서는 공적분 계수를 추상적인 개념으로만 다루어 보았고, 실질적인 추정방법에 대해서는 언급이 부족했던 것 같다.

페어트레이딩에서 공적분 계수는 투자 비율을 결정짓는 요소이기 때문에 매우 중요한 요소라 할 수 있다. 재무관리 측면에서는 시장모형으로 롱-숏 포트폴리오를 만들어내고, 이 포트폴리오가 시장중립모형이 되도록 비율을 결정한다. 따라서 투자 비율은 베타를 이용한 방법이 사용된다. 그러나 공적분 개념을 사용하는 Cointegration-Based 페어트레이딩에서는 베타의 개념을 사용하지 않고 공적분 계수를 이용하여 투자 비율을 결정한다.

Cointegration-Based 페어트레이딩은 공통추세모형 (Common Trend Model)의 이론을 기반으로 한다. 두 자산 간에 공통추세가 존재한다면 공적분 계수를 비율로 롱-숏을 구성하여 공통추세를 제거할 수 있고 (시장중립모형이 됨), 롱-숏 포트폴리오의 Pay Off는 추세가 없는 잔차 성분만 남게 된다. 만약 어떠한 비율로도 공통추세를 제거할 수 없다면, 두 자산 간에는 공통추세가 존재하지 않는 것이고 페어트레이딩의 대상이 될 수 없다. 공적분 계수로 공통추세가 제거된다면, 남은 잔차 성분은 정상성 (Stationary)이 높아지게 된다. 이 원리를 이용하면 공적분 계수를 추정해 볼 수 있다.

이론적인 내용은 다음 시간으로 미루고, 이번 시간에는 엑셀에서 공적분 계수를 간단히 추정하는 절차에 대해 알아보기로 한다. 공적분 계수를 추정하기 위해서는 수치해석을 사용해야 하므로, 엑셀의 수치해석 도구인 해찾기 (Solver) 기능을 활용한다.

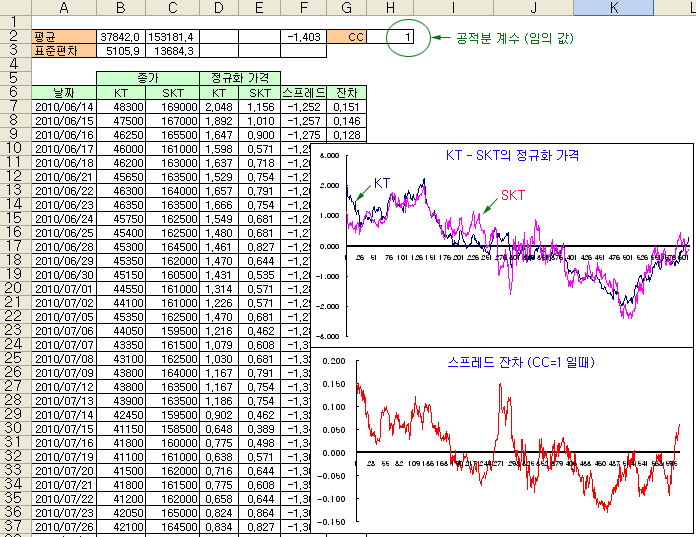
위 그림은 KT와 SKT의 일별 종가 (2010.6.14 ~ 2012.11.16)를 분석한 것으로, CC=1로 가정하여 스프레드를 그려본 것이다. CC=1로 가정했으므로, 투자 비율은 1:1로 가정한 것이고, 이때의 스프레드는 위의 그림과 같이 서서히 우하향하는 추세가 관측되므로 정상성이 높다고 할 수 없다. 여기서 스프레드는 공통추세가 제거된 잔차 성분을 의미하는 것이고, 스프레드에 추세가 발생한다는 것은 순수 잔차 성분만 남은 것이 아니므로, 두 자산 간의 공통추세가 서로 상쇄되지 못했음을 의미한다. 따라서 비율 1:1로 구성한 롱-숏 포트폴리오는 시장중립 특성을 갖지 못한다는 것을 의미한다.

CC 값이 변함에 따라 스프레드의 정상성도 달라지므로, CC값을 변화시켜가면서 스프레드의 정상성이 최대가 되는 지점을 찾아보자. 정상성이 최대가 된다는 것은 스프레드의 자기상관계수 (시차=1)가 최소가 된다는 것과 동일한 의미가 된다 (이 논리에 대해서는 다음 시간에 자세히 살펴본다). 그러면 스프레드의 자기상관계수 (Autocorrelation)가 최소가 되도록 CC를 결정해 볼 수 있다.

아래 그림은 엑셀의 해찾기 (Solver) 기능으로 스프레드의 자기상관계수가 최소가 되는 CC를 찾아내는 절차를 나타낸 것이다. (1) 스프레드 잔차의 자기상관계수 (시차=1)를 계산한다. 엑셀에 자기상관계수를 직접 계산하는 함수는 없으므로, 일반 상관계수를 구하는 CORREL() 함수를 이용한다. 아래 그림과 같이 CORREL(G7:G614, G8:G615)를 입력하면 G7과 G8, G8과 G9와 같이 자기 데이터의 이전 값과의 상관계수를 계산하게 되므로 자기상관계수가 된다. (2) 엑셀에서 도구->해찾기 (엑셀 2003 기준)를 실행하여 “목표셀” 이 위에서 계산한 자기상관계수를 가리키도록 한다. 그리고 “해의 조건” 을 최솟값으로 지정한다. (3) “값을 바꿀 셀” 에는 CC 값의 셀을 지정한다. 그러면 자기상관계수가 최소가 되도록 CC를 결정하는 것이 된다.

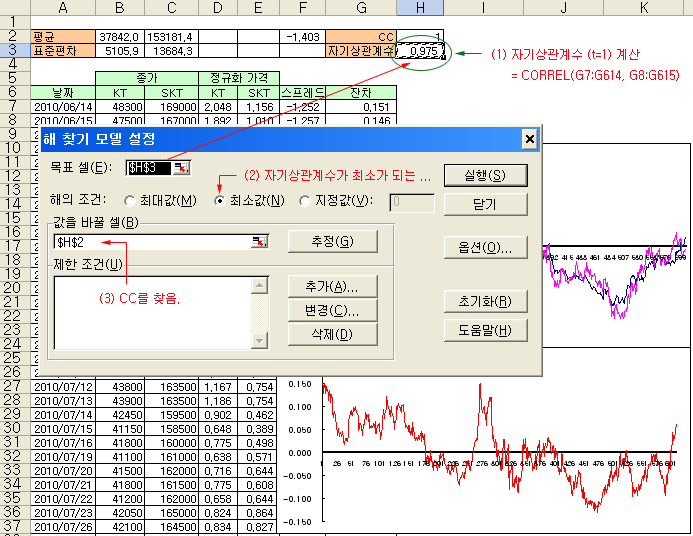
위와 같이 설정한 후 “실행” 을 누르면 아래 그림과 같이 CC=1.61774가 나온다 (약 CC=1.62). 이 값이 스프레드의 정상성을 최대로 만드는 CC 값이 된다. 육안으로 확인해 보아도 아래 그림의 스프레드가 위 그림의 스프레드보다 정상성이 훨씬 강하다는 것을 알 수 있다. 위나 아래로의 추세도 보이지 않고 0을 중심으로 위, 아래로 진동하는 모습이다

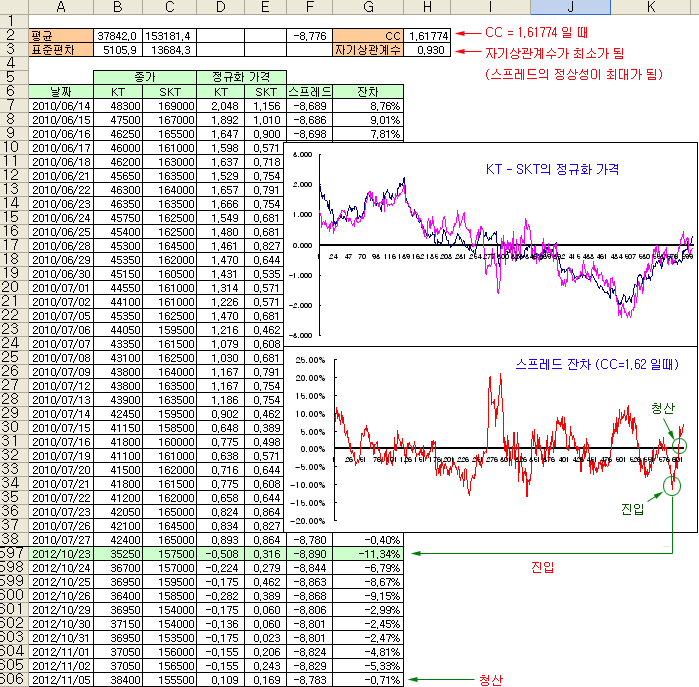
CC=1.62 의 의미는 KT:SKT의 투자 비율을 1:1.62로 적용하라는 의미이다. 이 비율로 롱-숏을 구성하면 공통추세가 서로 상쇄되고 잔차만 남는 (스프레드 = 잔차) 포트폴리오가 된다는 의미이다. 따라서 이 비율이 페어트레이딩의 최적 비율이라 할 수 있다.

이 비율대로 스프레드의 최근 저점에서 진입하여 균형점 부근에서 청산한 경우를 예를 들어보자. 최근 저점은 2012.10.23일 이고, 이때의 스프레드 잔차는 -11.34% 이다. 그리고 2012.11.05일 스프레드 잔차가 -0.71%일때 청산한 경우를 생각해 보자.

* 진입시

KT – 100 주 매수 : 35,250 * 100 = 3,525,000원 어치 매수

SKT – 3,525,000 * 1.62 = 5,710,500원 어치 매도–> 36주 매도 (5,710,500/157,500 = 36)

* 청산시

KT : (38,400 – 35,250) * 100 = 315,000원 수익

SKT : (155,500 – 157,500) * 36 = -72,000원 수익 (매도이므로)

* 총수익 = 387,000

* 수익률 = 387,000 / 3,525,000 = +10.95% (초기 투자금은 매수 금액만 적용함)

수익률은 위의 계산 결과와 같이 10.95% 이고, 이것은 스프레드의 차이인 -0.71% + 11.34% = 10.63%와 잘 일치한다. 이 결과는 1:1로 투자했을 때의 수익률보다 높은 결과가 나왔고 스프레드로 정상성이 높으므로 위험이 작다고 볼 수 있다.

공적분 계수를 설명하려면 시계열 분석 이론을 언급하여야 하지만, 여기서는 간단히 엑셀을 이용하여 최적 비율을 결정해 보았다. 실제로 이 절차는 실무에도 직접 적용이 가능한 방법이다.

이번 시간에는 절차와 결과 위주로만 살펴보았고, 다음 시간부터는 위의 논리가 합리적인 이유에 대해 차차 설명해 보기로 한다.

[출처]17. 공적분 계수 추정 방법|작성자아마퀀트