[금융수학] 7. 랜덤 워크와 브라운 운동 (Random Walk and Brownian Motion)

금융 수학 (7)

랜덤 워크 와 브라운 운동 (Random Walk and Brownian Motion)

주가의 흐름은 랜덤 워크 (Random Walk) 가설을 따른다고 한다. 랜덤 워크는 술 취한 사람이 비틀비틀 걸어가는 모습으로 묘사되기도 하는데, 앞으로의 방향을 예측할 수 없는 움직임을 말한다. 금융 이론을 전개하려면 주가의 모형을 설정해야 하는데, 랜덤 워크의 성질을 이용하여 모형화하면 주가의 실제 상황을 그런대로 잘 설명할 수 있다. 랜덤 워크의 수학적 성질을 따져보기 이전에 엑셀에서 이 과정을 먼저 살펴보자.

랜덤 워크 과정은 동전 던지기에서 앞면과 뒷면이 나오는 횟수를 누적해서 그려나갈 수 있다. 동전 던지기는 총 500번으로 하고, 동전의 앞면이 나오면 +1, 뒷면이 나오면 -1이라고 하고, 이것을 모두 더해가면서 그래프를 그려보면 아래 그림과 같이 랜덤 워크 과정을 그릴 수 있다. 마치 주가의 움직임처럼 보인다.

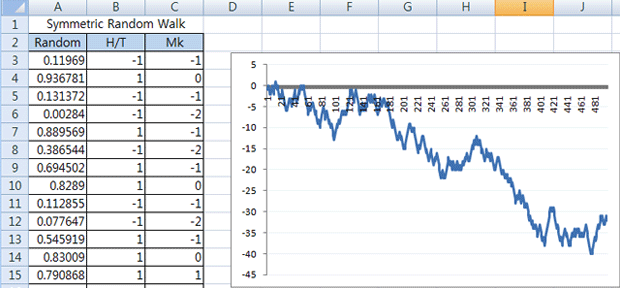
* 셀(A3) ~ 셀(A503) = RAND() ~ 0에서 1사이의 랜덤 숫자를 생성한다.

셀(B3) ~ 셀(B503) = if(A3 > 0.5, 1, -1) ~ 랜덤 숫자가 0.5 이상이면 “1”,

아니면 “-1” 을 표시한다.

~  “1”은 동전의 앞면, “-1″은 동전의 뒷면을 의미한다.

셀(C3) = B(3)

셀(C4) = C(3) + B(4)  ~ 셀(B)를 계속 누적시켜 나간다.

셀(C5) = C(4) + B(5)

.

.

F9 키를 눌러 RAND() 값을 재계산 하면 그래프의 모양이 바뀌게 된다. 아래는 바뀐 그래프들의 샘플이다. 마치 주가 차트처럼 움직이기 때문에, 이 성질을 이용하면 주가의 모형을 설정할 수 있다.

랜덤 워크 과정 (Random Walk)

위의 관계를 수식으로 표현해 보면 아래와 같다. 동전 던지기 실험 (w)에서 j 번째에서 동전의 앞면이 나오면, Xj = 1 이고, 뒷면이 나오면 Xj = -1 로 정하고, 1 번째부터 j 번째까지의 Xj를 모두 더하면 j 번째의 Mk 값이 된다. 이때 Mk 값을 Symmetric Random Walk 라고 한다.

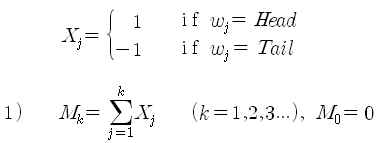
랜덤 워크도 확률과정이므로, 평균과 분산의 특성을 갖는다, 평균은 +1 과 -1의 조합으로 만들어 진 것이므로 0 이 나올 것이고, 그래프의 한 칸 단위의 분산은 위나 아래로 1 씩 움직이므로 1 이 나올 것이다. 두 단위의 분산은 2가 나올 것이고, k 단위의 분산은 k 가 나올 것이다. 이를 수식으로 나타내면 아래와 같다.

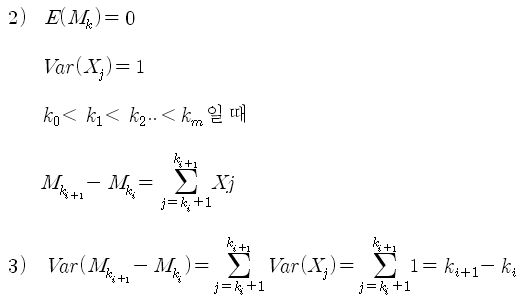
브라운 운동 (Brownian Motion), 위너 과정 (Wiener Process)

이번에는 동전 던지기 실험의 구간을 더 나누어서, 실험 사이사이에 또 여러 번의 동전 던지기를 수행 한다고 생각해 보자. 처음 실험을 1,2,3 … t 번째라고 순서를 매기고, 그 사이의 실험을 1,2,3…n 이라고 순서를 매기기로 해 보자. 이것은 t가 시간이라고 할 때 (1시, 2시, 3시,…), 그 사이에 분 (minutes)이 있다고 (1분, 2분 …) 생각해 보는 것이다. 그러면 위의 랜덤 워크 과정을 세분화해서 아래와 같이 식 4)로 표현할 수 있다.

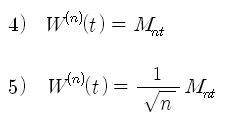
식 4)에서 n은 t 사이사이의 실험 횟수이다. t를 시간으로 생각하고, n을 분으로 생각하면 쉽게 개념을 잡을 수 있다. 식 5)는 식 4)의 Scale을 조정해 준 것으로, sqrt(n)으로 나누어 준다. Scale만 조정한 것일 뿐 다른 특성에는 영향이 없다. 식 5)를 Scaled Random Walk이라 부르고, n이 무한히 커질 때를 브라운 운동 (Brownian Motion) 혹은 위너 과정 (Wiener Process) 이라 부른다.

위너 과정도 엑셀에서 그림을 그려 보면 위의 엑셀 차트와 같이 될 것이다. 다만 실험 횟수가 더 많이 늘어나고, 스케일만 조정된 (y-축의 값이 줄어듦) 그래프가 나올 것이다.

위너 과정도 랜덤 워크 과정과 특성이 동일하므로 평균과 분산은 아래와 같다. 위너 과정의 평균은 0 이고, 분산은 dt 가 된다. 시점 0 부터 t 까지의 분산은 t가 되고, 표준편차는 sqrt(t)가 된다. 위너 과정의 변화량은 평균이 0 이고, 분산이 dt인 정규분포를 따른다. 이전 포스트에서 역사적 변동성을 계산할 때 일일 변동성 (일일 수익률의 표준편차)에 sqrt(252)를 곱해서 연간 변동성으로 환산한 이유가 바로 위너 과정의 변동성이 sqrt(t)에 비례하기 때문이다.

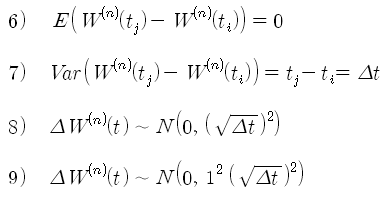
기하 브라운 운동 (Geometric Brwonian Motion) 과 주가 모형

주가의 특성에는 일정 범위의 변동성이 존재하고, 장기적으로 인플레이션 효과만큼의 (무위험 수익률) 상승효과가 존재한다. 따라서 무작위의 위너 과정만으로는 주식의 모형을 만들 수 없다. 무위험 수익률만큼 상승 (Drift)하는 추세에다가, 주가의 최근 변동성을 반영한 위너 과정의 효과를 추가하여 주가의 모형을 만든다. 위너 과정의 효과가 장기적 추세보다 더 크게 하락하면 장기적 주가도 하락할 수 있는 것이다. 단기 주가의 흐름은 무위험 수익률이 거의 0 에 가까우므로, 주가의 흐름은 추세 성분은 없고, 위너 과정 성분만 있게 될 것이다. 이를 고려하여 주가의 움직임을 표현한 것을 기하 브라운 운동 (Geometric Brownian Motion) 이라고 한다.

기하 브라운 운동을 아래의 식 10)으로 정의하고, 이를 연속적인 주가의 모형으로 설정한다. u는 t 기간까지의 무위험 수익률 (Drift)이고, 시그마^2 은 수익률의 분산을 의미한다. Wt는 위에서 정의한 t 시점까지의 위너 과정이다. t 시점의 주가 St는 초기 주가 S0 에 연속 복리 형태를 취한 형태이고, 수익률 (이자율) 에는 무위험 수익률과 위너 과정이 고려되어 있다. 이것은 일정한 복리 수익률로 주가가 증가하는 것이 아니라 위너 과정의 불확실성을 포함하여 주가가 상승하거나, 하락할 수 있는 형태를 가지고 있다. (유도 과정은 기하브라운운동과 내재변동성 참조)

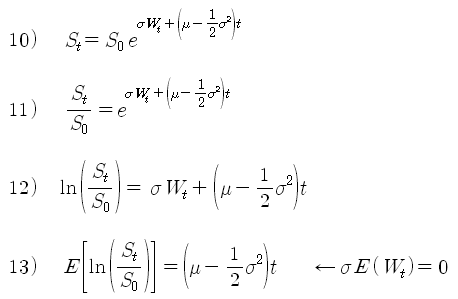
식 12)는 주가의 로그 수익률을 계산한 것이다. 위너 과정이 포함되어 있으므로, 총 수익률은 “+” 가 나올 수도 있고, “-” 가 나올 수도 있다. 식 13)은 평균 수익률을 계산한 것이다. 무위험 수익률 (u)과 변동성 (시그마)이 상수라면 식 12)의 평균을 식 13)과 같이 쓸 수 있다.

기하 브라운 운동으로 정의된 주가의 모형을 이용하면 다양한 이론들을 전개해 볼 수 있다. 다음 포스트에서는 이모형을 이용하여 엑셀에서 몬테카를로 시뮬레이션 (Monte Carlo Simulation)을 해 보도록 하겠다.

[출처]7. 랜덤 워크와 브라운 운동 (Random Walk and Brownian Motion)|작성자아마퀀트