[금융수학] 32. 기하브라운운동과 내재변동성

금융 수학 (32)

기하브라운운동과 내재변동성

[update 2016.11.24] 아래 기하브라운운동의 수식은 주가모형의 시뮬레이션과 ELS 상품의 이해 (3) 에 동영상으로 설명되어 있습니다.

내재변동성은 옵션의 시장가격을 이용하여 기초자산의 변동성을 역산한 것으로, 옵션 시장에 참여한 투자자들이 전망하고 있는 기초자산의 변동을 의미한다. 이번 시간에는 역산된 내재변동성의 근원적 의미를 추적해 보기로 한다. 즉, 내재변동성이 역산된 공식에서 내재변동성이 최초로 어디서 등장했는지를 추적해 보는 것이다. 이것을 추적하기 위해서는 먼저 기하브라운운동의 유도 과정을 살펴볼 필요가 있다.

1. 기하브라운운동 (Geometrical Brownian Motion : GBM)의 유도 과정

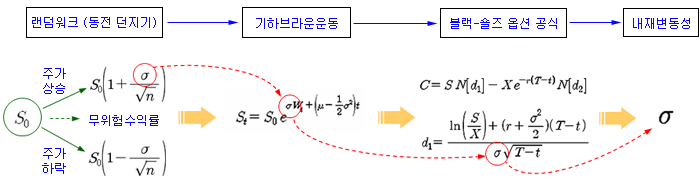
GBM을 유도하기 위해 주가의 움직임을 아래와 그림과 같이 설정해 보자. 주가의 움직임은 랜덤워크를 따르는 동전 던지기 게임으로 설정해 볼 수 있다. 최초 주가가 S0 일 때 (t=0), 다음 기의 주가는 (t=1) 오를 수도 있고, 떨어질 수도 있다. 동전 던지기 게임을 적용하여, 동전의 앞면이 나오면 주가가 상승하고, 뒷면이 나오면 주가가 하락하는 것으로 설정한다.

주가는 Drift (무위험 수익률, 인플레이션 등) 효과가 있기 때문에, 주가가 상승하든지 하락하든지 관계없이 매 기마다 Drift 만큼은 오르게 된다. 그리고 주가가 상승하거나 하락할 때는 매 기마다 주가 수익률만큼 오르거나 떨어지는 상황으로 설정하고, 주가 수익률은 (수익률의) 표준편차로 설정한다. 즉, 주가가 매 기마다 표준편차만큼 오르거나 하락하는 것으로 한다. (참고 : 주가의 순간 분산은 수익률의 제곱이므로, 순간 표준편차는 수익률이 된다). 여기서 Drift와 표준편차를 전체 기간의 단위로 정의하면 (연간 단위로 생각), 매 기 마다 적용되는 Drift와 표준편차는 1/n, 1/루트-n을 적용해 준다 (일간 단위로 환산한 것으로 생각). 단, 매 기에 적용되는 주가 수익률 (표준편차)은 모두 동일한 것으로 가정한다 (불합리하지만, 문제를 단순화 하기위한 가정임).

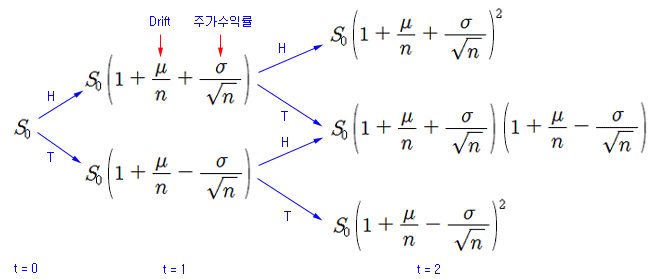
주가의 흐름을 위와 같이 설정하면 시간이 경과함에 따라 주가는 동전 던지기 게임과 동일한 형태로 전파하게 되어, 어떤 분포를 형성하게 된다. 주가가 전파되는 과정에 대한 일반항을 만들어 보면 주가 모형을 만들어 볼 수 있다. 아래 식 1)은 위 과정의 일반항이다 (t-시점의 주가에 대한 표현임). t-시점의 주가는 동전의 앞면이 나온 횟수만큼 상승 수익률이 적용되고, 뒷면이 나온 횟수만큼 하락 수익률이 적용되어 주가가 형성된다. 이제 이 일반항을 정리해서 주가의 모형을 만들어 보자.

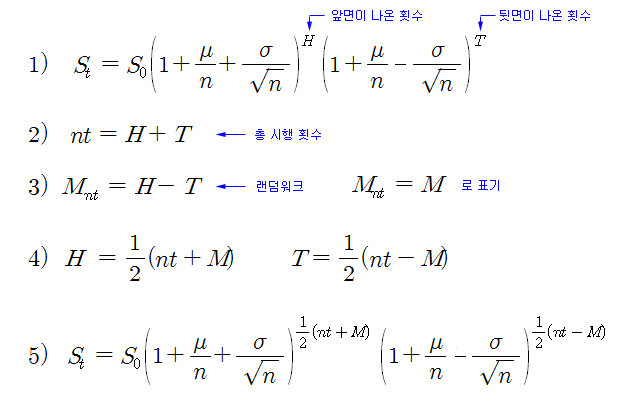
식 2)는 동전 던지기 게임의 총 횟수를 의미한다. 즉, 앞면이 나온 횟수와, 뒷면이 나온 횟수를 모두 더하면 총 횟수가 된다 (t-시점 까지 주가가 전파된 횟수). 식 3)은 랜덤워크의 정의식이다 (랜덤워크와 브라운운동 참조). 식 2)와 3)의 연립방정식을 풀면 식 4)가 되고, 식 4)를 식 1)에 대입하면 식 5)와 같이 주가 모형을 정리할 수 있다.

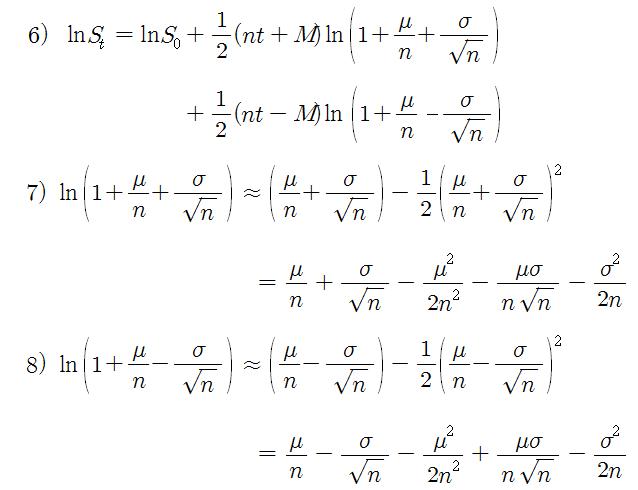
식 5)의 양변에 자연로그를 취하면 식 6)이 된다. 여기서 로그 항을 쉽게 풀기위해 테일러급수 (a=0)를 2차 항 까지만 적용한다 (Drift와 수익률은 모두 1보다 작은 수). 식 7) 과 8)은 로그 항에 대한 테일러 급수식이다. 식 7)과 8)을 다시 식 6)에 대입하고, 모두 전개한 후 정리하면 아래 식 9)가 나온다.

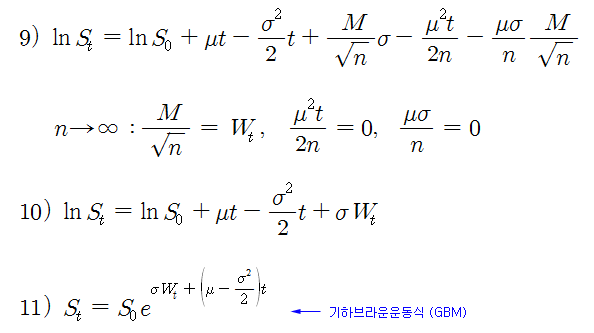
식 9)에서 동전 던지기 게임을 무한 번 수행하면, 랜덤워크 과정은 브라운운동 (혹은 위너과정)이 되고, 식 9)의 마지막 2개 항은 0 이 된다. 따라서 식 9)는 식 10)으로 표현할 수 있다. 식 10)의 양변에 지수를 취하면 식 11)이 되고, 이 식)이 바로 기하브라운운동 (GBM) 식이 된다.

여기까지 과정은 동전 던지기 게임을 이용하여 주가가 시간에 따라 전파되는 모형을 만들어 본 것이다. 식 11)의 주가 모형은 불확실성인 위너과정을 (Wt) 포함하고 있기 때문에, 결정론적인 식이 아니라 확률론적인 식이다. 이 식은 매 기마다 표준편차 (변동성)가 일정하게 적용되었다는 문제점이 있지만, 단순한 모형으로, 이용하기 편리하기 때문에 금융 분야에서 널리 사용된다. 예를 들어, 이 식을 이용하여 몬테카를로 주가 시뮬레이션을 만들어서 금융 상품을 평가 (설계) 하는 등에 활용되고 있다.

식 11)이 금융 분야에 널리 이용된다는 사실은 시사하는 바가 크다. 다시 언급하지만 식 11)은 단순히 맨 위에서 설정한 동전 던지기 게임으로부터 만들어 낸 식이다. 즉, 주가의 움직임을 홀-짝 게임으로 본 것이고, 이 식이 금융 분야에 널리 이용된다는 것은, 현대 금융 시장을 지배하는 기본 원리가 바로 홀-짝 게임이라는 것을 의미한다.

2. 내재변동성의 의미

내재변동성은 옵션의 시장가격을 이용하여 블랙-숄즈의 옵션 공식으로부터 계산한다. 그런데, 블랙-숄즈의 옵션 공식은 기하브라운운동을 이용하였고, 기하브라운운동은 맨 위에서 설정한 동전 던지기 게임을 이용하였다. 그렇다면 내재변동성을 계산한다는 것은 바로 동전 던지기 게임에서 설정한 주가의 수익률을 계산한 것이 된다. 즉, 내재변동성의 최초 출발점은 바로 동전 던지기 게임에서 설정한 주가의 수익률이다.

이제 내재변동성의 근본 출처를 알았으므로, 현재의 내재변동성을 이용해서 옵션 시장에 참여한 투자자들의 전망을 보다 정확하게 이해해 볼 수 있다. 아래 그림은 오늘의 (글을 쓰는 순간의) 시장 상황을 표시해 본 것이다. 오늘 코스피 지수는 1,980 이었고, VKOSPI는 14.2% 였다. 그리고 Drift는 기준 금리 2.5%를 적용해 보았다. VKOSPI 는 내재변동성을 대표하는 변동성지수이므로 이를 내재변동성의 대용치로 사용하였다.

VKOSPI 14.2% 는 향후 30 일간의 코스피200 지수의 평균 변동성을 연간 단위로 환산한 것을 의미한다. 따라서 VKOSPI 가 14.2%라는 의미는, 30일 후의 코스피 지수가, 상승한다면 2,077 이 되거나, 하락한다면 1,883이 될 것으로 전망된다는 의미이다. 즉, 옵션 시장의 참여자들은 위의 상황을 전망하여 옵션의 시장 가격을 형성하고 있다는 의미이다. 여기서 Drift 효과는 식 12)와 같이 위험중립확률에 적용해 보았다. 그러므로 30일 후 주가가 2,077이 될 확률은 52%이고, 1,883이 될 확률은 48% 가 된다. 그리고 30일 후의 주가 분포를 정규분포로 보면, 수익률이 1σ 지점이므로, 주가가 2,077 과 1,883 사이에 분포할 확률은 대략 68%가 된다. 요약하면, 내재변동성 14.2% 라는 숫자는 이러한 상황을 내포하고 있는 것이다.

이번 시간에는 기하브라운운동의 유도과정과, 내재변동성의 근본적인 의미에 대해 살펴보았다. 글 중에 다소 주관적인 내용도 포함되어 있으나, 크게 무리가 되는 내용은 없을 것으로 판단된다.

[출처]32. 기하브라운운동과 내재변동성|작성자아마퀀트