[금융수학] 33. 순간 변동성과 평균 변동성

금융 수학 (33)

순간 변동성과 평균 변동성

현대 금융시장에서 변동성이 차지하는 역할은 대단히 크다. 그리고 변동성을 표현하는 방법도 매우 다양하다. 일반적으로 변동성은 과거 일정 기간 동안 주가의 수익률에 대한 표준편차로 나타낸다. 즉, 일정 기간 동안 수익률의 분포가 평균으로부터 얼마나 떨어져 있는가를 계량화한 것이다. 평균 수익률로부터 많이 떨어져 있으면 변동성이 높은 것이고, 조금 떨어져 있으면 변동성이 낮은 것이다.

일반적으로 변동성은 과거 일정 기간 (T) 동안의 평균 변동성을 의미한다 (T를 얼마로 설정하느냐에 따라 평균 변동성은 다르게 측정된다). 1952년 마코비츠 이래로 평균 변동성은 식 (1)과 같이 주가의 수익률 분산으로 측정해왔다. 이 식을 1 ~ T 기간까지의 순간 변동성들을 평균한 것으로 생각해 볼 수도 있다. 그런데 순간 변동성처럼 보이는 항에 평균의 (x bar) 개념이 들어가 있다. 따라서 이 항을 순간 변동성이라고 보기는 어려울 것 같다. 주가 수익률의 시계열은 평균이 (거의) 0 이므로 x bar를 0 으로 근사시켜 생각할 수도 있다. 그러면 순간 분산은 t 시점의 수익률 제곱이 되고, 순간 변동성은 단순히 그날의 수익률이 되어 변동성이라는 개념이 없어진다. 따라서 이 식으로 순간 변동성을 이해하기는 어려울 것 같다.

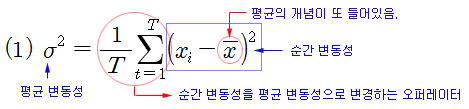
순간 변동성 혹은 현재의 변동성은 얼마인가? 오늘의 변동성은 단순히 오늘의 수익률인가?  내일의 변동성은 얼마로 예측되는가? 처럼 순간 변동성이라는 개념을 직관적으로 이해하기는 쉽지 않다. 그 이유는 분산의 개념으로 변동성을 생각하기 때문이다.

VKOSPI는 옵션의 시장가를 이용하여 KOSPI200 지수의 향후 30일 간의 평균 변동성을 예측한 지수이다. 향후 특정 시점의 순간 변동성은 잘 모르지만, 앞으로 30일 동안의 순간 변동성들을 모두 평균한 것이 바로 VKOSPI 지수의 의미이다.

VKOSPI 유도식을 이용하면 순간 변동성에 대한 표현을 얻을 수 있다. 식 (2)는 VIX 공식 유도과정의 식 (9)이다. 이 식의 좌변은 순간 변동성들을 모두 평균한 평균 변동성을 의미한다. 이 식을 이산식으로 표현하면 식 (3)과 같이 쓸 수 있다. 여기서 0 ~ T 기간 동안의 최종 로그 수익률은 중간의 로그 수익률 (0, 1, 2, 3, … T)을 모두 합한 것과 동일하므로 식 (2)의 최종 로그 수익률은 식 (3)의 로그 수익률들의 합으로 쓸 수 있다. 식 (3)을 정리하면 식 (4)로 쓸 수 있고, 이 식이 바로 순간 변동성을 일정 기간 (1 ~ T) 평균한 평균 변동성이 된다.

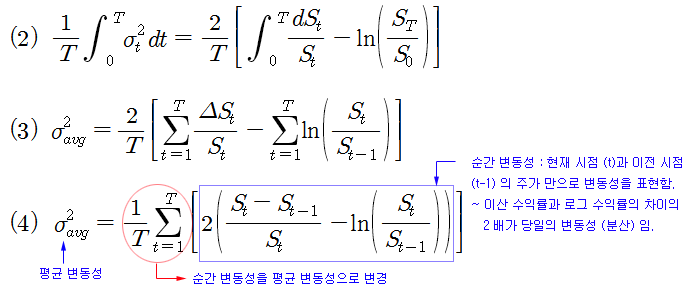
식 (4)의 대괄호 안의 표현을 순간 변동성으로 정의할 수 있다. 왜냐하면, 현재시점 (t)과 이전 시점 (t-1) 만으로 변동성 (분산)을 표현하고 있기 때문이다 (식 (1) 처럼 x bar 와 같은 표현이 없다. 일정 기간이라는 개념도 없다). 즉, 오늘의 변동성 (분산)은 오늘의 이산 수익률과 로그 수익률 (연속 수익률)의 차이에 2를 곱한 것과 같다. 변동성이 크다는 것은 이산 수익률과 로그 수익률의 차이가 크다는 것을 의미하고, 변동성이 작다는 것은 두 수익률의 차이가 작다는 것을 의미한다. 식 (4)를 이용하면 순간 변동성을 직관적으로 이해해 볼 수 있다.

아래 그림은 주가가 동일한 크기로 한번 오르고, 한번 떨어진 경우의 최종 pay-off의 변화이다. t=0 시점에 100원짜리 주식이, t=1 시점에 +10% 상승하고, t=2 시점에 -10% 하락하면 최종 주가는 99원이 된다 (이산 수익률 기준). 반대의 경우로 t=1 시점에 -10% 하락하고, t=2 시점에 +10% 상승해도 결과는 동일하다. 변동성이 증가해서 +20 ~ -20% 로 변하는 경우와, +30% ~ -30%로 변하는 경우를 관찰해 보면 이산 수익률과 로그 수익률의 격차는 점점 커지고 최종 주가는 더 크게 영향을 받는다 (그림에 로그 수익률은 표시되어 있지 않음).

아래 그림은 최근 1년간 KOSPI200 지수의 역사적 변동성을 계산해 본 것이다. 평균 변동성 (1)은 식 (1)로 계산한 것이고, 평균 변동성 (2)는 식 (4)로 계산한 것으로, 결과가 거의 동일하다. 즉, 식 (4)도 변동성에 대한 표현이 된다는 것을 알 수 있고, 분산이 아닌 방법으로도 변동성을 표현할 수 있다는 것을 알 수 있다. (상세 계산식은 첨부 파일 참조)

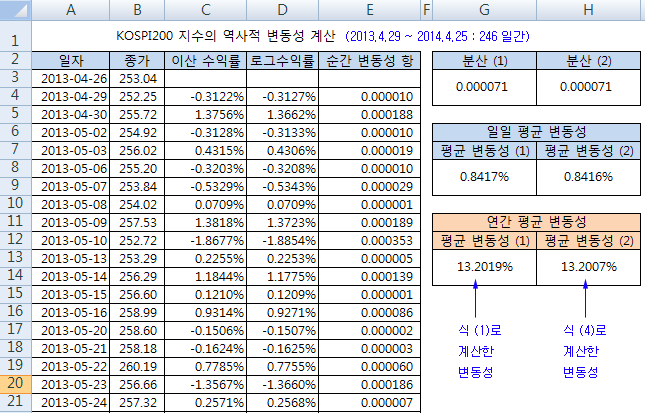
식 (4)가 가지는 의미를 요약해 보면, 순간 변동성을 표현할 수 있다는 점과, 변동성은 이산 수익률과 로그 수익률의 차이와 관계가 있다는 점, 그리고 분산이 아닌 다른 관점으로도 변동성을 측정할 수 있다는 점이다.

다음 시간에는 GARCH 모형을 이용하여 순간 변동성으로 미래의 평균 변동성을 예측하고, VKOSPI로 예측한 결과와 비교해 보기로 한다.

[출처]33. 순간 변동성과 평균 변동성|작성자아마퀀트