[금융수학] 34. GARCH 모형에 의한 변동성 추정

금융수학 (34)
GARCH 모형에 의한 변동성 추정

이번 시간에는 GARCH 모형으로 기초자산의 변동성을 추정하여 VKOSPI 지수와 비교해 보기로 한다. VKOSPI 지수는 옵션의 시장가를 이용하여 간접적으로 기초자산의 변동성을 추정한 것이고, GARCH 모형은 기초자산의 가격 변화를 이용하여 직접적으로 기초자산의 변동성을 추정한 것이다. 따라서 두 결과는 동일하거나 아주 밀접한 관계에 있어야 한다.

그러나 GARCH 모형은 분석기간에 따라 변동성이 다르게 추정된다. 분석기간을 길게 잡아서 변동성이 높았던 시기가 포함된다면, 향후 변동성도 높을 것으로 예측될 것이고, 분석기간을 짧게 잡고, 그 시기에 변동성이 낮았다면, 향후 변동성도 낮게 추정될 것이다. 즉, GARCH 모형에 의한 변동성은 분석기간에 따라 가변적이며, 분석기간을 얼마로 설정하는 것이 타당한지는 결정하기가 어렵다.

반면에 VKOSPI는 과거 자료를 사용하는 것이 아니라, 현재 시장에 참여하고 있는 옵션 거래자들의 거래 행위로부터 추출한 것이므로, 과거의 분석기간과는 무관하다. 따라서 GARCH 변동성과 VKOSPI를 직접 비교한다는 것은 큰 의미가 없다. 한 가지 의미를 찾아볼 수 있는 것은, 분석기간을 얼마로 설정할 때, GARCH 변동성과 VKOSPI 지수가 같아지는가? 이다. 즉, VKOSPI 지수를 참조하여 GARCH 모형의 적정 분석기간을 결정해 볼 수 있다 (단, 분석기간이 유일하게 나오는 것은 아님). 옵션 거래자들이 과거 이 기간 동안의 변동성을 참고한다고 볼 수 있다.

GARCH(1,1) 모형 설정

GARCH(1,1) 모형은 아래와 같이 설정할 수 있다. 일반적인 분산식 1) 에서 가중치와 장기 평균 분산 (V)을 고려하면 식 5)를 만들 수 있다. 식 5) 는 t 시점의 분산은 t-1 시점의 수익률 제곱과 t-1 시점의 분산으로 설명할 수 있다는 의미이다. 즉, 오늘의 분산은 어제의 수익률 제곱과, 어제의 분산으로 설명할 수 있다고 가정한 식이다.

모수 추정

식 5)에서 수익률인 x와, 변동성인 σ 는 과거의 측정값이고, ω, α, β 는 추정할 파라메터 (모수) 이다. ω, α, β를 안다면, 과거의 측정치로부터 현재의 변동성을 계산할 수 있고, 미래의 변동성도 추정해 볼 수 있다.

모수 (ω, α, β)를 추정하는 방법으로는 최우도 추정법 (Maximum Likelihood Estimation : MLE)을 이용한다. 식 6)은 계산의 편의를 위해 만들어진 로그 우도 함수이다. 이 식에서 괄호안의 식을 최대로 만드는 ω, α, β를 추정하면 된다. (MLE에 대한 자세한 내용은 시계열 분석을 참조 바람)

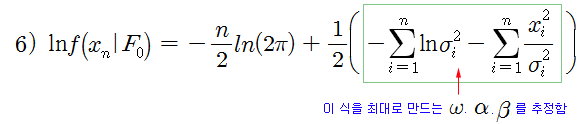
변동성 예측

VKOSPI는 현재부터 30일 후까지의 평균 변동성을 의미하고 (30일 후의 순간 변동성이 아님), VIX (VKOSPI) 공식의 유도 과정의 식 9)로 표현된다. 따라서 GARCH 모형도 n 일 후의 전방 예측값이 아닌, n 일 후까지의 평균 변동성으로 예측해야 한다 (그래야 VKOSPI와 비교가 가능하다).

GARCH(1,1) 모형에 의한 n 일 후까지의 평균 변동성은 아래의 과정으로 예측할 수 있다. 식 13) 이 t 부터 n 까지의 평균 변동성이므로, VIX (VKOSPI) 공식의 유도 과정의 식 9)와 의미상 동일한 표현이다. 식 13)을 풀면 식 15)를 얻을 수 있다 (등비수열의 합 공식이 사용됨). 과거 자료를 이용하여 ω, α, β를 추정하면 식 15)로 미래 평균 변동성을 추정할 수 있다. 여기서 V는 분석기간 동안의 전체 분산이고, n 은 예측하고자 하는 미래의 기간으로 VKOSPI와의 비교를 위해서는 n=30 으로 한다.

변동성 예측 실례 (엑셀)

KOSPI200 지수의 과거 1년간 데이터 (2013.5.10. ~ 2014.5.9.)를 이용하여 향후 30일 간의 평균 변동성을 예측하면 아래와 같다. 식 6)을 이용하여 식 5)의 모수들 (ω, α, β)을 추정한 후, 식 15)로 향후 30일 간의 변동성을 예측한 결과이다 (상세 내역은 첨부파일 참조).

GARCH(1,1)에 의한 예측 결과는 13.18%이고, 2014.5.9. VKOSPI 종가는 10.71% 였다. VKOSPI가 GARCH 모형보다 현저히 낮다. 장기 평균 분산 (V)은 13.20%로 GARCH 모형은 향후 변동성도 V 근처에서 형성될 것이라고 주장하고 있다. 사실 GARCH 모형도 평균 회귀 특성으로 인해, 현재 변동성이 V 보다 낮다면 V 쪽으로 갈 것이라고 예측하게 된다 (시계열 분석의 한계 ??).

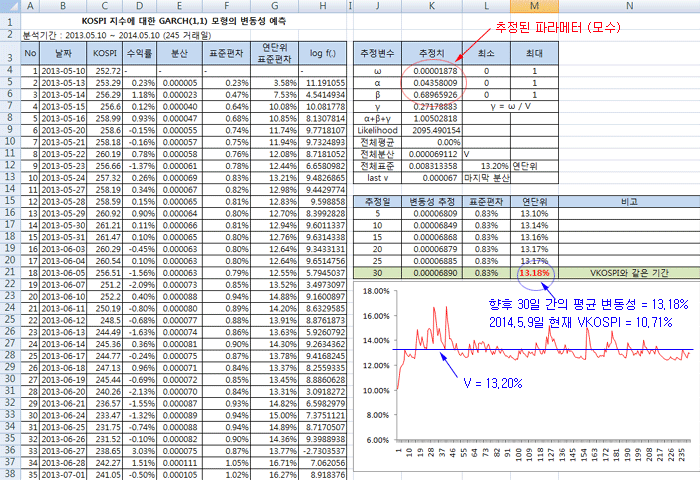
처음 계획은 분석기간을 바꿔가면서 GARCH 모형과 VKOSPI가 같아지는 기간을 찾아보려는 것이었다. 그러나 VKOSPI 지수가 너무 낮기 때문에 분석기간을 아무리 바꾸어도 두 지수가 같아질 수는 없다. 이것은 현재 옵션 시장의 참여자들은 과거 어느 때 보다도 향후 변동성이 낮을 것으로 기대한다는 것을 의미한다.

그럼 GARCH 모형과 VKOSPI 지수 중 어느 것이 더 향후 변동성을 잘 표현하고 있을까? 우열을 가리긴 어렵겠지만 옵션 시장이 충분히 효율적이라면 VKOSPI 지수가 더 의미가 있어 보인다. 그러나 VKOSPI 지수를 계산할 때 옵션 시장의 정보가 충분히 반영되었는지에 대해서는 생각해 볼 필요가 있다.

S&P500 옵션은 행사가격이 충분히 많지만 (100여개 정도), KOSPI200 옵션은 행사가격의 개수가 많아야 20개 정도이고, 정보가 풍부한 ATM~OTM 옵션은 약 10개 정도에 불과하다. 따라서 VIX 산출에 사용된 정보량과 VKOSPI 산출에 사용된 정보량에는 큰 차이가 있어 보인다. 만약 VKOSPI에 사용된 정보량이 부족하다면 VKOSPI 지수의 신뢰성도 재고해 보아야 한다.

GARCH-VKOSPI-정보량의 관계를 좀 더 분석하려면 VIX와 GARCH 모형에 의한 S&P500 지수의 변동성도 분석해 볼 필요가 있지만 여기서는 이 정도로 마무리하기로 한다. 이 부분에 대해서는 관심 있는 독자들의 활약을 기대해 본다.

[출처]34. GARCH 모형에 의한 변동성 추정|작성자아마퀀트