[금융수학] 39. ATM Straddle의 특성 분석

금융 수학 (39)

ATM Straddle의 특성 분석

이번 시간에는 변동성 거래 (Volatility Trading) 중 옵션을 이용한 ATM Straddle 전략의 특성에 대해 살펴보기로 한다. ATM Straddle 은 행사가격이 등가격 (At-the-money)으로 동일하고 (S = X), 만기가 동일한 콜옵션과 풋옵션을 동시에 매수한 전략으로 변동성을 매수한 형태의 전략이다 (C + P).

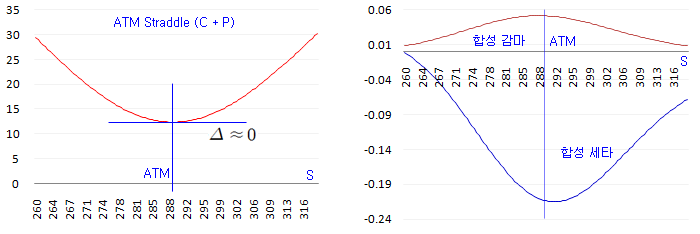
ATM Straddle 의 특성은 아래 그림으로 간단히 살펴볼 수 있다. 좌측 그림은 C + P 의 손익구조이다. S 가 크게 오르거나 크게 내리면 수익이 발생한다. C, P 모두 등가격 옵션이므로 합성 델타는 0 에 가깝다. 우측 그림에서는 ATM 지점의 합성 감마와 합성 세타의 절대값이 최대가 됨을 알 수 있다 (부호가 반대임). 즉, ATM Straddle은 최대의 감마 수익을 얻는 대신, 최대의 시간가치 (세타)를 지불하는 구조이다.

Black-Scholes 공식을 이용해서 위의 특징을 수학적으로 확인해 보자. 식 1)은 콜옵션에 대한 Black-Scholes 편미분 방정식이고, 식 2)는 Greeks를 사용하여 식 1)을 다시 표현한 것이다. 식 3)은 풋옵션에 대한 표현이다 (풋옵션과 콜옵션의 표현은 동일하지만 경계조건이 다르므로 해가 다르게 나온다 : 맨 아래 [참고사항] 참조). 식 4)는 ATM Straddle인 C + P 포트폴리오의 표현식이고, 합성 Greeks로 표현하면 식 5)가 된다. 식 5)에서 합성 델타는 0에 가까우므로 ATM Straddle은 델타 중립 (Delta neutral) 포지션이 되고, V의 손익구조는 세타 (θ)와 감마 (Γ)의 변화로 설명할 수 있다.

식 5)에서 C + P 포트폴리오인 V의 손익은 시간가치 항만큼 감소하고, 변동성 항만큼 증가한다. ATM에서 시간가치와 변동성 항은 모두 최대가 된다 (부호는 반대).

ATM Straddle의 합성 델타 (Δ)

ATM Straddle의 합성 델타는 0 에 가까우나, 정확히 0 은 아니다. 그 이유는 ATM 콜옵션의 델타가 정확히 +0.5 가 아니기 때문이다. 콜옵션의 델타는 N[d1] 이고, 풋옵션의 델타는 N[d1] – 1 이다. 따라서 합성 델타는 식 6)과 같이 2*N[d1] – 1 이 된다. 합성 델타가 0 이 되려면 N[d1] = 0.5 가 되어야 하지만 N[d1] > 0.5 이기 때문에 합성 델타도 0 보다 큰 값이 된다.

합성 델타의 근사치를 계산하기위해, S = X, rt = 0 인 경우를 생각한다. 식 7)에 이 조건을 대입하면 식 9)와 같이 N[d1]의 근사치를 계산할 수 있고, 식 11)과 같이 합성 델타 (Δ)의 근사치를 얻을 수 있다. 앞에서 언급한대로 합성 델타는 0 보다 약간 큰 값이 나온다. 변동성이 20% (σ = 0.2) 이고, 잔존기간이 20일 (t = 20 / 252 = 0.079) 이라면 합성 델타는 0.022 정도로 작은 값이 나온다.

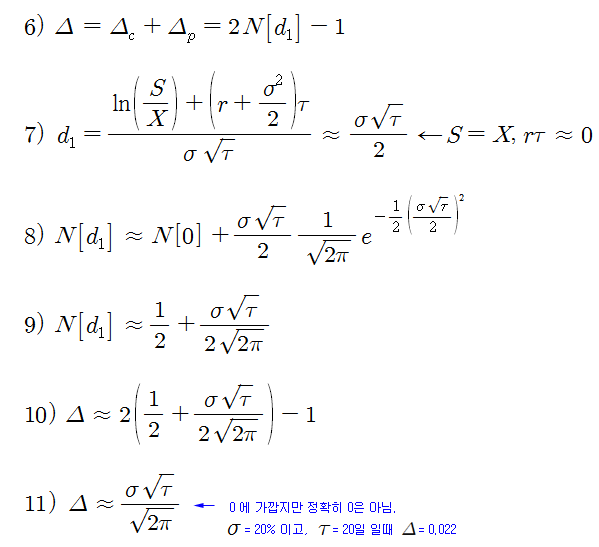
ATM Straddle의 합성 감마 (Γ)

콜옵션의 감마와 풋옵션의 감마는 동일하므로 ATM Straddle의 합성 감마는 식 12) 가 된다. ATM 옵션에 대한 d1 은 0 에 가까우므로, 식 12)의 exp() 항은 1 에 가깝게 되고, 합성 감마는 근사적으로 식 14)가 된다. 식 14)에서 델타 (Δ)와 감마 (Γ)는 서로 반비례 관계에 있으므로, Δ가 0 에 가까울수록 Γ가 커진다는 것을 알 수 있다. 즉, 델타-중립 포지션인 경우 감마가 최대가 된다 (위의 그림으로 확인한 것과 동일함).

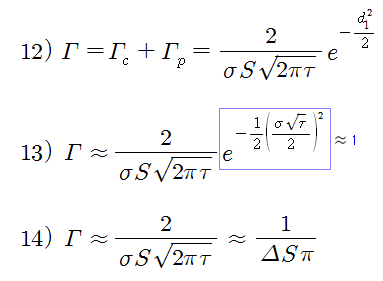
ATM Straddle의 세타 (θ)

콜옵션의 세타는 식 15) 이고, 풋옵션의 세타는 식 16) 이다. 그리고 ATM Straddle의 합성 세타는 식 18)로 쓸 수 있다. ATM 위치에서는 식 17)의 관계가 (근사적으로) 성립하므로, 식 18)에 식 17)의 관계를 대입하면, 합성 세타는 식 19)로 쓸 수 있다. 식 19)에서 합성 델타는 0 에 가까우므로 ATM Straddle의 합성 세타는 근사적으로 식 20)으로 표현할 수 있다.

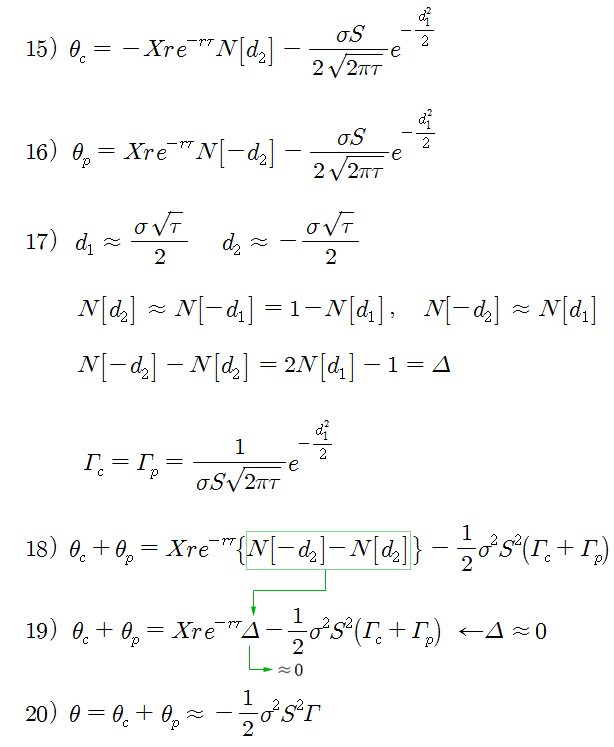
식 20)에서 세타는 식 5)의 변동성 항과 같은 표현이다 (부호는 반대). 이 것은 델타-중립 옵션에서는 세타를 감마의 대용치로 쓸 수도 있다는 것을 의미한다. 여기서 식 20)의 우변 항에 포함된 σ는 내재변동성 (Implied Vol.)을 의미하고, 식 5)의 σ는 실현변동성 (Realized Vol.)을 의미하는 것으로 해석한다 (뒤에 설명 있음).

ATM Straddle의 손익구조

ATM Straddle 포트폴리오 (V)를 테일러 급수로 표현하면 식 21)로 쓸 수 있다. 단, V(S, t) 이고 (σ는 일정), S에 대한 2차식 까지만 고려한다. 식 21)에서 합성 델타는 0 이므로, V의 변화량은 식 22)가 된다 (여기서 Δ는 합성 델타가 아니라, 변화량 (difference)을 의미한다).

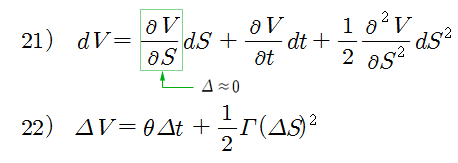
식 22)는 ATM Straddle (V)의 변화량이고, 시간 (Δt) 이 지나면서 세타 (θ) 만큼의 시간가치가 감소하고, 주가가 변할수록 (ΔS) 감마 (Γ)가 관련된 양만큼 증가한다. 이 변화를 그림으로 표현하면 아래와 같다.

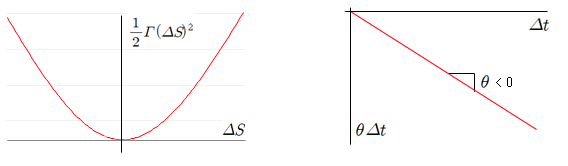
현재 시점 (t0)의 주가가 S 이면, Δt 시간 이후의 주가는 [그림-A]와 같이 표현할 수 있다 (기하브라운 운동 (GBM) 참조). 따라서 Δt 시간 이후의 주가의 변화인 ΔS 는 식 23)이 된다. 식 23)을 식 22)에 대입하면 식 25)를 얻을 수 있다. 식 25)의 세타는 식 20)을 이용하여 감마로 표현할 수 있다. 그런데 세타는 t0 시점의 변동성 (t0 시점의 내재변동성)의 영향만큼 감소한다. 즉, 식 20)의 σ 는 내재변동성이 된다. 그리고 t1 시점의 ΔS 는 t1 시점의 실제 변동성 (실현변동성)의 영향을 받는다. 즉 식 25)의 우변에 있는 σ 는 실현변동성이 된다. 따라서 식 25)에 식 20)을 대입하면 식 26)을 얻을 수 있고, 식 26)을 정리하면 식 27)이 된다. 식 27)은 이전 시간에 살펴본 분산스왑 (Variance Swap)과 유사한 표현이다. 즉, ATM Straddle은 분산스왑과 동일한 형태의 변동성 거래임을 알 수 있다. 물론 ATM Straddle은 Static hedge 이므로 S의 변화가 크지 않은 짧은 시간 동안에만 성립하는 식이다.

여기까지 ATM Straddle의 합성 델타, 합성 감마 그리고 합성 세타의 특성을 살펴보았고, ATM Straddle이 변동성 거래가 됨을 수식으로 확인해 보았다. 물론, 맨 위의 그림 하나로 거의 모든 것을 설명할 수 있지만, 수식을 통해 좀 더 자세히 확인해 보았다. 다음 시간에는 델타-헤징 옵션 전략에 대한 특성을 살펴보기로 한다.

[참고사항] 식 3)의 증명

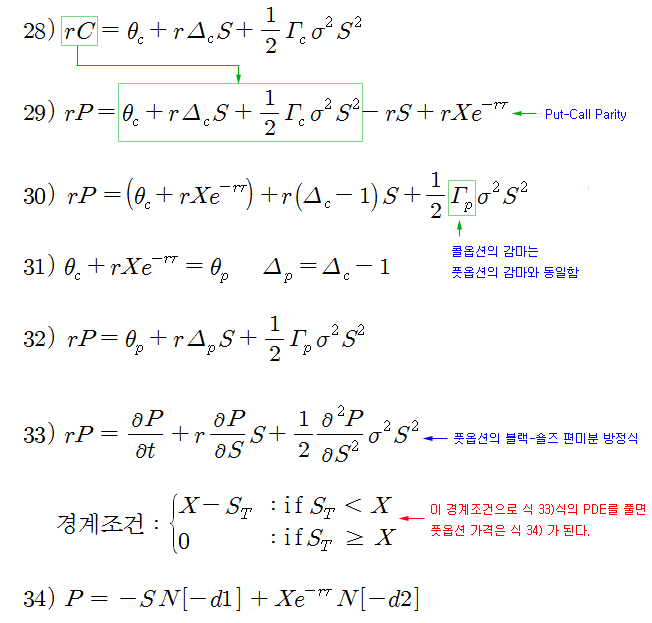
[출처]39. ATM Straddle의 특성 분석|작성자아마퀀트