[알고리즘 트레이딩/전략편 ] 15. 옵션의 통계적 차익거래 : Skewness and Kurtosis Trades (1)

알고리즘 트레이딩 (Algorithmic Trading) – 전략 (15)

옵션의 통계적 차익거래 : Skewness and Kurtosis Trades (1)

(옵션의 프리미엄과 기대손익과의 관계)이전 포스트에서는 옵션의 행사가별 가격관계를 이용하여 무위험 차익거래 기회가 존재하는지 살펴보았고, 거래가 활발한 등가격 (ATM)에서는 무위험 차익거래 기회가 발생하지 않음을 확인해 보았다. 이번 시간에는 무위험은 아니더라도 유리한 지점을 포착하여 포지션을 진입하는 통계적 차익거래에 대해 살펴보도록 하겠다.

아래 그림은 이전 포스트에서 살펴본 얕은 내가격 부근에서의 옵션의 프리미엄 변화이다. 빨간색 원으로 표시된 지점이 무위험 차익거래 가능지점 이었으나 거래가 활발하지 않아 포지션 진입이 불투명한 지점이었다. 이번에는 오른쪽 그림과 같이 프리미엄이 낮은 지점에 관심을 가져 보도록 하겠다. 알고리즘으로 등가격대나 내가격대에서 프리미엄의 변화를 관찰하여 평균보다 낮은 지점을 포착한다면 훨씬 유리한 지점에서 포지션을 구축할 수 있을 것이다. 즉, 동일한 포지션으로 기대손익은 동일하게 유지하면서, 프리미엄을 낮게 지불하면 일종의 통계적 차익거래라 볼 수 있다.

이번에는 옵션의 프리미엄과 기대손익의 관계에 대해 알아보자. 옵션을 매입하여 미래에 기대할 수 있는 기대수익을 현재가치로 환산한 것이 현재의 옵션 프리미엄이다 (금융수학/옵션의 기대손익을 통한 이론가 계산편 참조). 즉, 기대수익을 크게 하려면 현재 프리미엄을 높게 지불해야 한다. 그래야만 공정한 시장이 된다.

아래 그림은 위의 참조 (금융수학편)에서 살펴본 옵션의 기대수익과 기초자산의 확률분포와의 관계이다. 그림 (가)와 같이 C-P 합성 포지션을 생각해 보자. 행사가격이 X2인 콜옵션을 매입하고, 행사가격이 X1인 풋옵션을 매도한 포지션으로 향후 주가가 오를 것으로 기대하고 있는 포지션이다. 만약 합성 포지션과 기초자산의 확률분포 f(S)의 위치가 그림 (가)와 같이 되어 있다면, 주가가 X1이 될 확률은 f(1)이 되고, X2가 될 확률은 f(2)가 된다. 확률이 높아지면 기대심리가 높아지므로 프리미엄도 높게 형성될 것이다.

그림 (나)는 그림 (가)와 동일한 포지션이지만 확률분포상의 위치가 다르다. 주가가 X1이 될 확률은 낮아지고, X2가 될 확률은 높아진 그림이다. 이 상태에서는 주가가 X2보다 커질 확률이 50% (육안 상으로)나 되므로, C-P 합성 포지션의 기대수익이 높아진다. 그러나 매도해야할 X1의 확률이 낮아지므로 풋 프리미엄이 낮아져 풋 옵션을 낮은 가격에 매도해야 한다. 또한, 매입해야할 X2의 확률은 높아지므로 콜 프리미엄이 높아져 높은 가격에 콜을 매입해야 한다. 즉, 합성 프리미엄이 높아지는 것이다. 따라서 시장이 정상 상태에 있다면 그림 (나)와 같이 높은 기대수익을 얻으려면 높은 프리미엄을 지불해야하고, 그림 (가)와 같이 낮은 프리미엄을 지불하려면 기대수익을 낮추어야 한다.

시장은 항상 정상 상태를 유지할까? 그렇다면 무위험이건 통계적이건 차익거래 기회는 전혀 없다. 그러나 때로는 시장이 정상적이지 못한 상태가 될 수도 있다. 아래 그림은 시장의 비정상 상황을 가정해서 그려본 것이다. 그림 (가)는 기초자산의 확률분포가 정상보다 우측으로 치우친 모습이고, 그림 (나)는 가운데가 뾰족하게 올라온 모습이다. 만약 확률분포가 아래 그림과 같이 왜곡된다면 프리미엄과 기대수익의 관계가 깨질 수 있다.

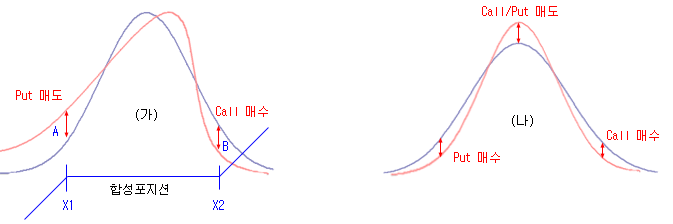
그림 (가)를 살펴보면, 행사가격 X1의 확률은 정상보다 높아져 있는 상태이고, X2의 확률은 낮아져 있는 상태이다. 그러면 매도해야할 풋 프리미엄이 높은 상태가 되고, 매입해야할 콜 프리미엄은 낮은 상태가 될 것이다. 즉, 동일한 기대수익에 대해 합성 프리미엄이 낮아지는 것이다. 알고리즘으로 이런 순간을 포착해서 진입한다면 동일한 기대수익에 대해 낮은 프리미엄을 지불하기 때문에 훨씬 유리한 상태가 되고, 바로 통계적 차익거래가 되는 것이다. 이러한 차익거래를 왜도/첨도 차익거래 전략 (Skewness and Kurtosis Strategy)이라고 한다.

그림 (나)에서는 가운데 부분의 확률이 높은 상태이므로 콜이나 풋의 현재 프리미엄이 정상보다 높게 형성된 경우이다. 반면에 양쪽으로는 정상보다 확률이 낮은 상태가 되어, 콜과 풋의 현재 프리미엄이 낮게 형성된 경우이다. 이 경우에는 가운데 지점의 콜이나 풋은 매도하고, 오른쪽의 콜과, 왼쪽의 풋은 매입하면, 유리한 포지션이 될 것이다.

이러한 관계는 이전 포스트에서 살펴본 행사가별 옵션가격의 관계 (Relationship)에서는 잘 드러나지 않는다. 예를 들어 앞에서는 X1, X2, X3의 관계가 틀어질 때 차익거래를 기대한 전략이었으나, 행사가격별로 큰 차이는 없지만 전체적으로 조금씩 오른쪽이나 왼쪽으로 치우쳐져 있거나, 위나 아래로 솟아 있는 상황은, 앞에서 본 전략으로는 검출하기 어려울 것이다. 따라서 이 전략은 행사가별로 전체적인 틀을 관찰하여 차익거래 기회를 포착해 보려는 것이라 할 수 있다.

그림 (가)와 (나)를 보면 옵션 시장 참여자들의 기대심리를 엿볼 수 있다. 그림 (가)는 시장 참여자들이 현재 주가보다 약간 높은 지점에 몰려 있고, 더 높은 지점에는 몰려있지 않으므로, 참여자들은 주가가 약간은 더 올라갈 것이나, 그렇게 많이 올라가지는 않을 것으로 예상하고 있다고 해석할 수 있다. 또한 왼쪽 부분을 보면 주가가 떨어진다면 많이 떨어질 것으로 보고 있다고 볼 수 있다. 그림 (나)는 주가가 현재 부근에 머물러 있을 것으로 예상하고 있다고 볼 수 있다.

알고리즘으로 차익거래 기회를 포착하기 위해서는 옵션의 프리미엄을 직접 관찰해서 낮은 지점을 포착하는 방법이 있을 수 있고, 확률분포를 관찰하여 왜곡된 지점을 포착하는 방법이 있을 수 있다. 프리미엄이 확률분포에 따라 결정되기 때문에, 확률분포를 관찰해 보면 간접적으로 프리미엄에 대해 알 수 있다.

프리미엄의 크기는 기초자산의 가격변화에 영향을 받으므로 프리미엄을 직접 관찰하는 방법은 정확성이 떨어진다. 반면에 확률분포의 형태는 기초자산 가격에 영향을 받지 않으므로 (확률분포의 위치는 영향을 받는다), 형태 자체는 일정하게 유지된다. 따라서 확률분포를 관찰하여 차익거래 기회를 포착하는 것이 더 의미가 있다고 볼 수 있다.

그러면 확률분포를 관찰한다는 것은 무슨 의미인가? 이 부분에 대해서는 금융수학/옵션의 행사가 민감도 및 SPD 공식유도편과 (State Price Density) 관련하여 다음 포스트에서 살펴보도록 하겠다.

참고자료 : Dynamics of State Price Densities

Skewness and Kurtosis Trades

[출처] 15. 옵션의 통계적 차익거래 : Skewness and Kurtosis Trades (1)|작성자아마퀀트