News & Events

1 step TD의 step을 증가시켜 나가면서 n 까지 보게 되면 n step TD로 일반화를 할 수 있습니다. 만약 step이 무한대에 가깝게 되면 MC와 동일하게 될 것입니다.
2 step TD 에서의 업데이트 방식은 첫번째 보상과 두번째 보상 그리고 두번째 상태에서의 value function의 합으로 업데이트가 됩니다.

TD(0) 가 n이 1인 1-step TD입니다.
앞에서 이야기한 업데이트 방식에 대한 내용을 수식으로 표현을 한 것입니다. 이를 n step에 대하여 일반화를 하면 중간에 식이 됩니다.
n step TD에서의 value 함수는 n step에서 얻은 총 보상에서 기존 value 함수값과의 차이를 알파만큼 가중치하여 더함으로서 업데이트가 되게 됩니다.
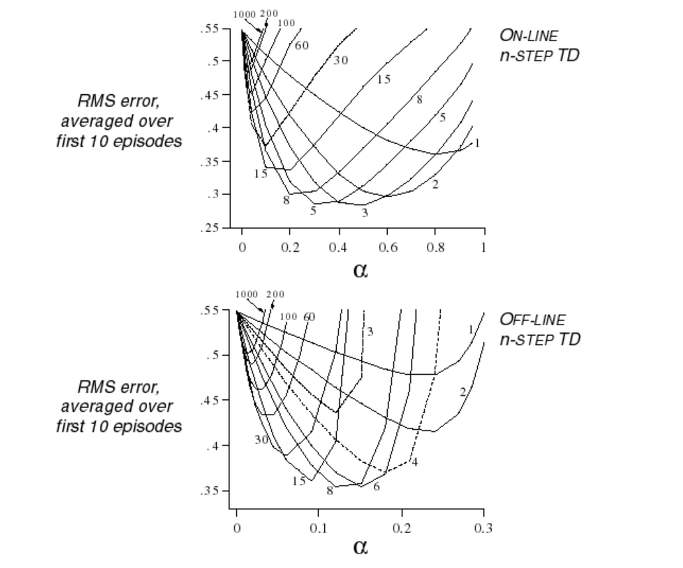
그럼 n 이 몇일때가 가장 최고의 결과를 나타낼까요? 그에 대한 실험이 위의 그래프입니다.
실시간 업데이트 하는 온라인 방식, 에피소드 완료후 업데이트하는 오프라인 방식에서 비슷한 결과로 나타나며, n 이 커질수록 에러가 큰것을 볼 수 있습니다. 별로 안좋은것이죠.
3~5 의 step size 혹은 6~8 의 step size가 좋은것 같습니다.

n step 에서의 보상을 다른 값으로 평균을 낼 수 있습니다. 그런데 step이 다른 2 step 과 4 step에서의 평균을 내어보면 위와 같은 식이 될 것입니다. 이 두가지의 결합하여 효율적으로 만들수 있을까요?
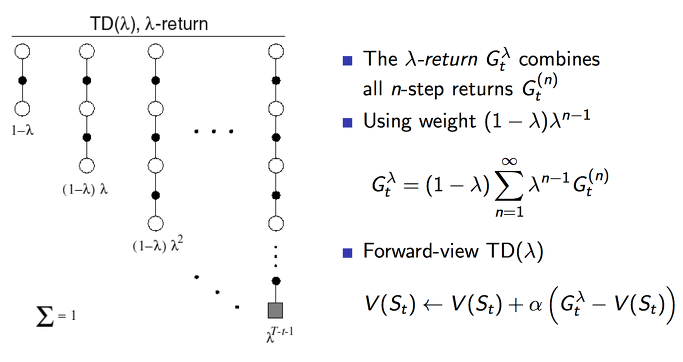
답은 가능하다 입니다.
여기서 람다 보상은 모든 n step까지의 가중평균된 보상입니다. 기존에 n step에서 사용한 보상은 총합이였습니다. 이렇게 평균을 사용하는 방식은 오류를 더 낮춰줄 수 있습니다.
람다의 총합이 1이 되도록 하기 위해서 (1 – 람다) 계수로 노멀라이즈를 하여 0부터 1까지의 값을 갖도록 합니다. 그리하여 이 람다는 n step이 커질수록 보상에 대한 값을 감소시키게 작용합니다.
마지막에 공식이 TD lamda 의 value 함수입니다.
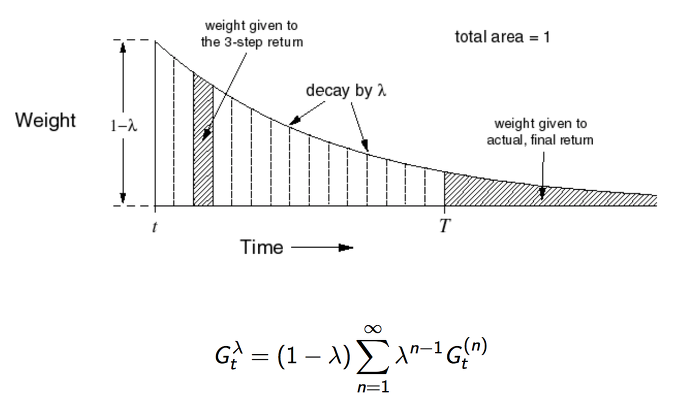
step 시간이 흐를수록 weight 가 지수형태로 감소를 하는 것을 볼 수 있습니다. 그리고 이들의 총합은 1이 됩니다. 지수형태의 가중치를 사용하는 것이 알고리즘의 연산에 효율성을 주고 메모리를 덜 사용하게 되는 이점이 있다고 합니다.
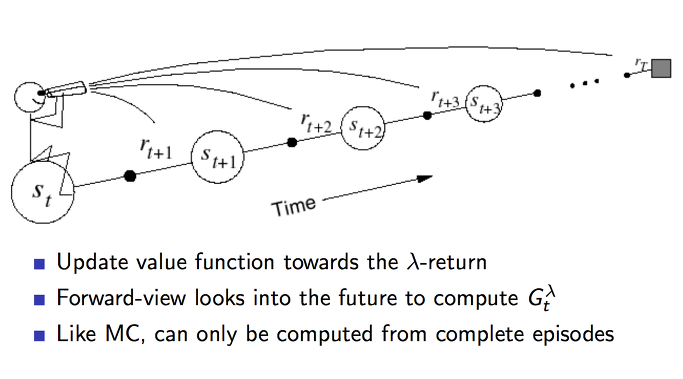
value 함수가 업데이트 되는 과정을 도식화한것입니다. 동일하게 n step 까지 도달하고 나서 얻은 보상들을 람다 보상을 구해서 업데이트 하게 됩니다.
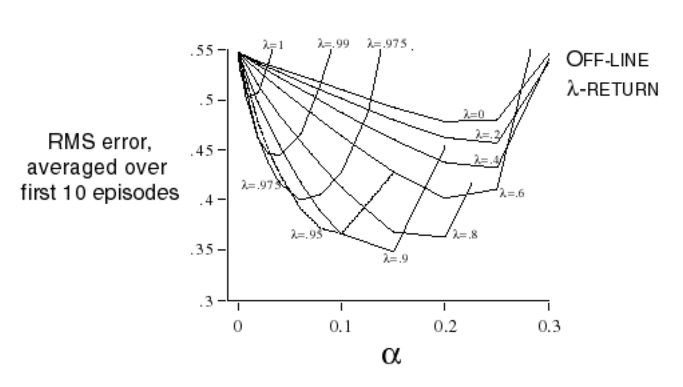
이전에 실험과 동일하게 해보면 위와 같은 그래프로 람다가 9 정도에서 좋은 것을 볼 수 있습니다. 람다가 1일때에는 MC가 되고 0일 경우에는 TD(0)가 됩니다.
bias와 variance의 trade off를 고려해서 적절한 값으로 사용하면 좋을 것입니다.

정방향에서의 관점에서 보면 이론적입니다. 반대방향에서의 관점에서 보면 컴퓨터적이게 됩니다. 반대 방향으로 보면 TD lamda 알고리즘은 온라인 방식과 같이, 매 step 마다 업데이트가 됩니다.
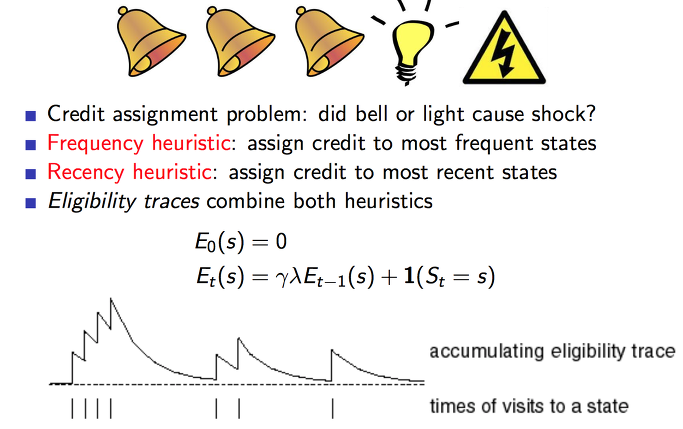
이전에 예제를 다시보면 위에서 번개가 발생한 이유가 종 때문일까요? 라이트 때문일까요? 자주 발생한 것이 영향이 큰지 최근에 발생한 것이 영향이 큰지를 결합하여 사용할 수 있습니다.
하나의 특정한 state를 방문하는 횟수에 따라서 Eligibility traces를 해보면 위 그래프와 같이 됩니다.
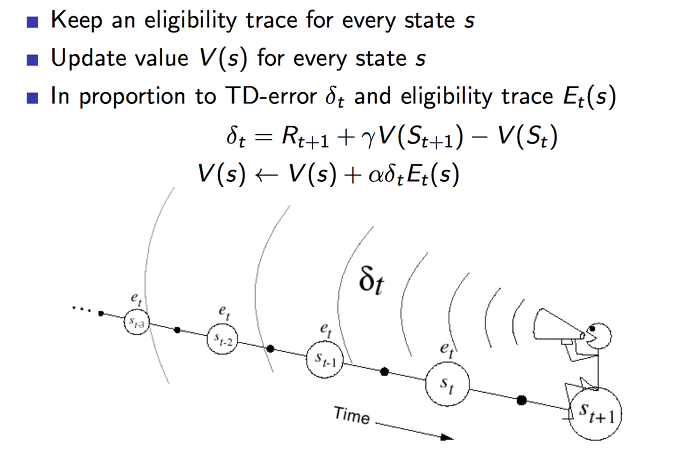
이를 적용해보면 각 state마다 업데이트가 발생이 될때 TD 에러의 비율 만큼 업데이트를 가중적용하는 것으로 할 수 있습니다. 이것은 에피소드의 길이보다 짧은 기억을 하는 단기 메모리 같은 역할을 합니다.

람다는 얼마나 빨리 값을 감소시키는가를 의미합니다. 람다가 0의 값이 되면 완전 가파르게 decay가 발생할 것입니다. 결국 현재 state의 value 함수만 업데이트가 되며 이는 TD(0)와 동일한 방식이 됩니다.

반대로 람다가 1이 되면 전체 에피소드를 모두 커버하게 됩니다. 그래서 오프라인 업데이트와 같이 될 것이고 이는 MC와 같은 방식이 됩니다.
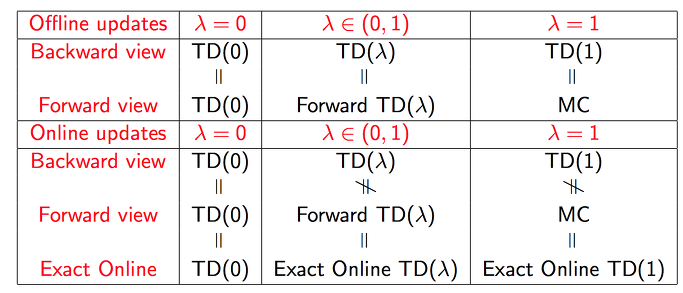
지금까지의 내용들을 최종적으로 정리를 하면 표와 같이 됩니다.


