[기술적분석] 12. 최적 매도 시점의 문제

기술적 분석 (12) 최적 매도 시점의 문제

주식을 보유한 상태에서 과연 최적의 매도 시점을 알 수 있을까? 오래전부터 많은 사람들이 이 문제의 답을 찾기 위해 고민한 흔적들이 많이 보인다 (Optimal stopping time 혹은 Optimal selling time). 주가를 랜덤워크로 보고 확률적으로 가장 적절한 매도 시점을 찾아보는 것이다. 이 문제의 풀이를 기술적으로 이해하기 위해서는 편미분 방정식 (PDE) 같은 어려운 수학 지식이 필요하지만 (확률제어 분야 등의 지식이 필요함), 여기서는 이론보다는 직관적인 해석을 통해 최적 매도 시점의 의미를 살펴보기로 한다.

우선 아래와 같은 경우에 대해, 상식적인 수준에서 최적 매도 시점에 대해 생각해 본다. 아래 그림들은 Drift (인플레이션)는 모두 동일하지만 변동성이 다른 경우의 주가 차트이다. 그림 A는 주가의 변동성이 거의 없고 Drift만 존재하는 경우이다. 이 경우에 최적 매도 시점이 존재할까? 존재할 수가 없다. 주가가 지속적으로 오르기만 한다면 주식을 매도할 이유가 전혀 없기 때문이다. 주식을 샀다 팔았다 해 봐야 별 이득이 없다.

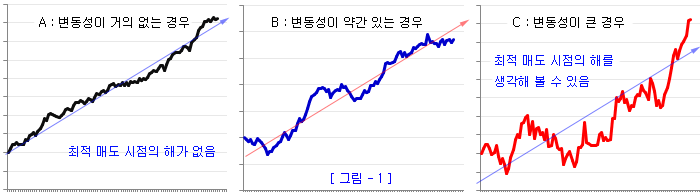
그림 B는 변동성이 약간 증가한 경우이다. 이 경우는 어떨까? 계속 보유하는 것이 좋을지, 올랐을 때 팔았다가, 떨어질 때 다시 사는 것이 좋을지… 잘 모르겠다. 그림 C는 변동성이 크게 증가한 경우이다. 이 경우는 주식을 계속 보유하는 것 보다는 올랐을 때 잠시 팔았다가, 떨어질 때 다시 사는 것이 좋아 보인다. 즉, 최적 매도 시점은 변동성과 밀접한 관계가 있어 보인다.

이론적인 결론도 상식과 잘 부합하는 것 같다. 그림 A의 경우 최적 매도 시점의 해는 불능으로 나온다 (해가 없다). 그러나 그림 C의 경우는 어떤 형태라도 해가 나오기는 한다. (이 해가 실무적으로 의미가 있는지는 논외로 한다). 즉, A와 C 사이에서 변동성이 어느 정도로 증가하면 최적 매도 시점의 해가 나타나기 시작한다.

최적 매도 시점을 다룬 논문들은 많지만 비교적 쉬워 보이는 (?) 두 논문 (Reference [1], [2])을 살펴보았다. 내용을 다 이해하진 못했지만 저자가 이야기하려는 바와 결론 부분을 나름대로 이해해 보았다. 논문 [1]은 단순 랜덤워크 (B)에서의 최적 매도 시점에 대한 것이다. 단순 랜덤워크이므로 Drift나 변동성에 대한 고려는 없다.

아래 식은 논문 [1]에서 제시한 최적 매도 시점의 해이다. t = 0 시점에 주식을 매수하고, t = 1 시점까지만 주식을 보유하는 경우이다. 0 < t <1 사이에 매도 조건이 발생하면 그 시점에 주식을 매도한다. 만약 t = 1 시점까지 매도 조건이 발생하지 않으면 t = 1 시점에는 무조건 청산 (매도)해야 한다. 주가에 해당하는 랜덤워크를 B, t 시점의 랜덤워크를 Bt 라고 하자. 그리고 t 시점까지 랜덤워크의 최대 지점을 St (전 고점), t = 1 시점까지의 (전체 구간) 최대 지점을 S1 (최고점) 이라하면, 최적 매도 시점에 대한 식을 아래와 같이 쓸 수 있다.

식 1)은 최적 매도 시점을 풀기위한 목적 함수이다. V는 보유한 주식의 가치 (Value) 함수이고, V는 S1과 Bτ의 차이가 최소 (infimum)일 때의 가치로, Bτ가 최고점 (S1)에 가까울수록 V는 커진다. 즉, t = 0~1 사이의 최고점에서 매도할 때 (t = τ)의 가치가 최대 가치가 되고, t = τ 가 바로 최적 매도 시점이 된다. 식 2)는 q = 2일 때 (mean-square error), 식 1)의 목적 함수를 풀어 최적 매도 시점 (τ)을 계산한 것이다. t = 0~1 사이에서 (St – Bt) 가 z * sqrt(1-t) 보다 큰 시점에 매도하는 것이 가장 효과적이라는 의미이다. 그리고 q = 2일 때 수치해석으로 계산한 z 값은 1.123 이다 (논문 [1]에 의하면). 즉, 현재 주가 (Bt)와 전 고점의 차이가 1.123 * sqrt(1-t) 보다 크면 매도하라는 의미이다.

이 결과를 기하학적으로 살펴보면 아래 그림과 같다. 주가에 해당하는 랜덤워크는 파란색선 (B)이고, 전 고점을 이은 선은 빨간색선(S) 이다. 그리고 전 고점에서 현재 주가를 뺀 값이 녹색선 (St – Bt)이고, z * sqrt(1-t)를 계산한 선이 보라색 곡선이다. 이 상태에서 최적 매도 시점은 녹색선이 보라색 곡선을 뚫고 올라갈 때이다. 즉, (St – Bt)가 z * sqrt(1-t) 곡선보다 클 때이다. 결과적으로 볼 때, 최고점에서 매도하면 좋겠지만, 그 순간에는 이 지점이 최고점인지, 앞으로 더 오를지 알 수 없으므로 결과적 최고점에서 매도하는 것은 불가능하다. 아래 예는 최고점을 지나 어깨 지점에서 매도하는 것이 가장 효율적이라는 것을 보여준다.

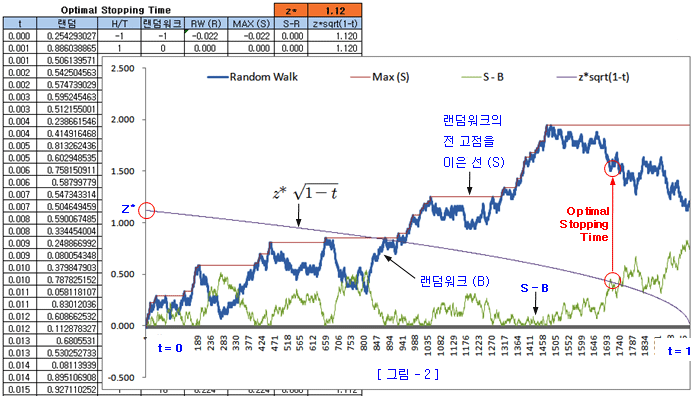
이번에는 z * sqrt(1-t) 곡선의 의미를 살펴보자. 주식을 매수한 시점 (t = 0) 에서는 만기까지 (t = 1) 시간이 많이 남았으므로 (기회가 충분히 있으므로) 곡선의 y 성분이 높다. 즉, 처음에는 녹색선이 곡선을 뚫을 가능성이 작다. 만약, 주식이 지속적으로 상승한다면 전 고점 (St)과 주가가 같이 상승하므로 그 차이가 작아지기 때문에 녹색선은 낮아진다. 따라서 주가가 지속적으로 상승하면 주식을 계속 보유하게 된다. 시간이 지남에 따라 곡선은 낮아지고 녹색선이 곡선을 뚫을 가능성은 점차 높아지므로 주식을 매도할 가능성이 높아진다. 만기가 되면 (t = 1) 곡선은 0 이 되므로 무조건 매도 (청산) 하게 된다.

주가만 본다면 이 결과는 기술적 분석의 데드크로스 (Dead cross)와 유사하므로 (어깨에서 청산한다는 점에서), 크게 얻은 정보는 없지만, 이론적으로 데드크로스가 최적 지점이 될 수 있다는 것을 이해할 수는 있을 것 같다.

위의 경우는 주가가 오른 경우만 본 것이다. 만약 주가가 하락한다면 최적 매도 시점은 최적 손절 시점이 될 것이다. 이 부분에 대해서는 첨부된 엑셀 자료로 시뮬레이션 해 보면 확인해 볼 수 있다.

이번에는 [그림 – 1]에서 제시한, Drift와 변동성이 존재하는 경우에 대해 살펴보자. 이 경우는 기하브라운운동 (GBM)에 대한 최적 매도 시점을 생각해 보아야 한다 (참고 논문 [2]).

식 1)의 목적 함수는 식 3)과 같이 쓸 수도 있다. 현재 주가 (V)와 전 고점 (S)의 비율로 (차이가 아닌) 정의해도 의미상 동일하다. 항상 St > Vt 이므로 (St 가 고점이므로 항상 주가보다 크거나 같다), 그 비율 (V / S)이 클수록 현재 주가가 전 고점에 가까이 있다는 의미이다. 따라서 식 3)의 목적 함수를 풀어서 최적 매도 시점인 τ를 구하면 된다.

식 4)는 기하브라운운동 (GBM)의 표현으로 Drift (α) 와 변동성 (σ)이 있는 주가의 표현식이다. 식 5)는 목적 함수인 식 3)을 풀어서 최적 매도 시점 (τ)을 구한 결과이다. 여기서는 t = 0 ~ T 까지의 기간을 고려한다 (T는 최대 보유기간, 혹은 만기를 의미함). 만약 Drift (α)가 변동성 제곱의 반보다 크다면 주식을 계속 보유하라는 의미이고, [그림 – 1]의 A 경우에 해당한다. 즉, 변동성보다 Drift 효과가 더 크므로 주식을 계속 보유하는 것이 더 낫다는 의미이다. 만약 변동성 제곱의 반이 Drift보다 크다면 τ = 0 이다. 이 의미는 즉시 매도하라는 의미이고 [그림 – 1]의 C 경우에 해당한다. 만약 변동성 효과와 Drift가 같다면 τ = any time, 즉, 아무 때나 팔아도 모두 최적 시점이 된다는 의미이다. 즉, 변동성과 Drift가 같은 지점이 주식을 보유해야할지, 팔아야할 지에 대한 분기점이 되는 것이다 ([그림 -1]의 B 경우).

예를 들어 어떤 주식 시장의 Drift = 2.5% 이고, 변동성 = 22.4% 라면, 변동성 제곱의 반 = 2.51% 이므로, 주식을 계속 보유하는 것 보다는 떨어졌을 때 팔고, 오르면 다시 사는 전략이 유효할 것이다. 만약, 변동성이 22.4% 이하라면 팔고 사는 것보다는 장기간 보유하는 것이 더 나을 것이다 (우리나라의 주식 시장은 어떨까 ???).

최적 매도 시점은 주식의 Drift와 변동성에 따라 달라진다. 그렇다면 Drift 정도의 수익을 목적으로 하는 장기 투자자는 변동성을 싫어할 것이고, 잦은 거래를 통해 초과 수익을 목적으로 하는 투자자는 변동성을 선호할 것이다. “초과 수익의 원천은 변동성인 Risk 다” 라는 말과도 잘 부합한다. 즉, 변동성이 어느 정도는 있어야 매매를 통한 초과 수익을 기대할 수 있다.

이번 시간에는 두 편의 논문을 통해 최적 매도 시점의 의미에 대해 살펴보았다. 그런데 [그림 – 2]의 신호를 이용한 매매가 과연 성과가 있을까? 의문이 든다. 다음 시간에는 시뮬레이션을 통해 성과 분석을 해 보기로 하겠다.

첨부파일: 최적매도시점

Reference :

[1] Jesper Lund Pedersen. Optimal Prediction of the Ultimate Maximum of Brownian Motion.
[2] S.C.P. Yam, S.P. Yung, W. Zhou (2010). Optimal selling time in stock market over a finite time horizon.

[출처]12. 최적 매도 시점의 문제|작성자아마퀀트