[기술적분석] 15. Trailing Stop의 특성 분석

기술적 분석 (15)

Trailing Stop의 특성 분석
이번 시간에는 Trailing Stop의 특성을 분석한 논문 한 편을 소개해 보기로 한다 [1]. 1995년 Glynn과 Iglehart는 “Trading Securities Using Trailing Stops” 라는 논문에서 Trailing Stop 모형의 기대수익, Risk, 평균 청산기간 등을 계산하였고, 최적 Stop Loss (L)의 수준이 존재하는지 여부를 확인해 보았다.

아래 그림은 단순 랜덤워크 과정이다 (이산모형). 주가가 상승하면 +1 증가하고, 하락하면 -1 감소하는 과정이다. 주가가 이 과정을 따른다고 가정하고, L = 2 라고 가정해보자. 즉 매수 진입 이후 주가가 전고점에서 2 단위 하락하면 청산한다고 가정한다.

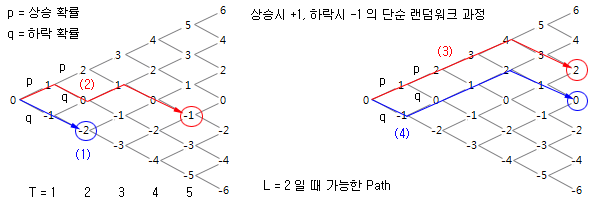
이 과정에서 주가는 어느 경로로든 갈 수 있다. 주가가 (1)번 경로로 갔다면, 진입직후 2 단위 하락했으므로, 2 기간 만에 -2의 손실이 발생한다. (2)번 경로는 5 기간 만에 -1의 손실이 발생하고, (3)번 경로는 6 기간 만에 +2의 수익이 발생하고, (4)번 경로는 수익도 손실도 발생하지 않는다. 이 과정은 오른쪽으로 무한히 확산되므로, 무수히 많은 경로가 존재한다.

이 그림에서 L=2 인 모든 경로를 파악해서, 평균 수익 (기대 수익)과 평균 청산 기간을 계산하면 아래 식이 된다. 논문 [1]에서는 복잡한 과정을 거쳐 아래 식들을 유도하였으나, 여기서는 결과만 살펴보기로 한다.

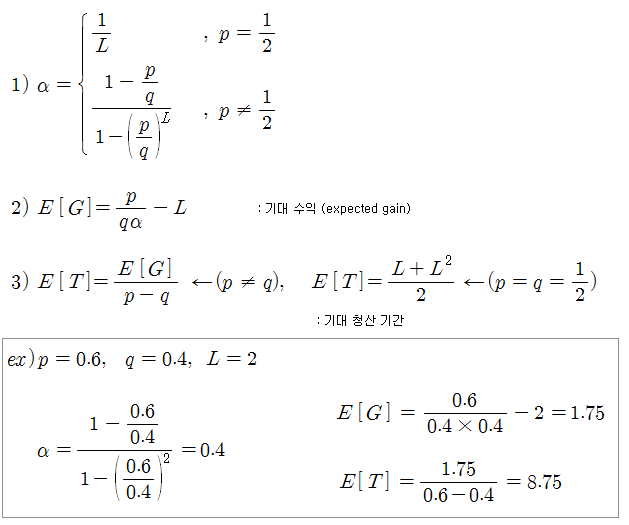
식 2)는 모든 경로에 대한 평균 수익 (기대 수익)이다. 여기서 p와 q는 각각 상승확률과 하락확률을 의미한다. 식 2)에서 p=q=1/2 이라면 기대 수익, E[G] = 0 이 된다. 이것은 임의 종목을 임의 시점에 매수한 후 Trailing Stop으로 청산한다면 수익을 기대할 수 없다는 것을 의미한다. 만약 p > q 라면 E[G] > 0 이 된다. 이것은 적절한 진입전략으로 p > q 인 종목이나 시점을 선택한 후 Trailing Stop을 적용하면 수익을 기대할 수 있다는 것을 의미한다. 예를 들어, 한 계좌에서 임의 시점에 선물을 매수하고, 동시에 다른 계좌에서 동일 선물을 매도한 후 모두 Trailing Stop을 적용한다고 생각해 보자. 선물이 오른다면 한 쪽에서는 수익이 발생하고 다른 쪽에서는 손실이 발생할 것이다 (선물이 내려도 한 쪽은 수익). Trailing Stop은 손실은 작고, 수익은 크므로 차익이 발생할 것으로 생각할 수도 있지만 위 논리에 위배되므로 결국 수익이 발생할 수 없다 (손실은 작지만 빈번함. 두 계좌 모두 손실로 끝날 확률이 높음).

식 3)은 평균 청산 기간이다. L=2 이고 p=q=1/2 라면 평균 청산 기간, E[T] = 3 이다. 즉 단순 랜덤워크에서는 평균적으로 3 기간 만에 청산하게 된다는 것을 의미한다 (그림으로는 설명이 잘 안됨. why ??). 만약 p=0.6, q=0.4, L=2 라면 평균적으로 8.75 기간 만에 1.75의 수익을 기대할 수 있다.

이 과정을 단순 랜덤워크가 아닌 기하브라운운동 (GBM) (연속모형)에 적용하면 기대수익과 평균 청산기간은 아래와 같다. 주가가 drift (μ)와 변동성 (σ)을 가지고 GBM을 따르는 경우이다. 단, μ 와 σ 는 % (rate)가 아닌 주가 단위이다 (μ = 주가 차의 평균, σ = 주가 차의 표준편차).

만약 μ = 0 이라면 식 5)의 E[G] = 0 이 된다 (로피탈 정리). 이것도 주가에 drift가 존재하지 않는다면 Trailing Stop으로 수익을 기대할 수 없다는 것을 의미한다 (이산모형의 p=q 의 경우와 동일). μ = 0.5 이고 (주가가 단위 기간 당 평균적으로 0.5 pt씩 상승함), σ = 1, L = 2 라면 평균적으로 8.8 기간 만에 4.4의 수익을 기대할 수 있다. 적절한 진입전략으로 μ > 0 인 조건을 충족시킬 때만 Trailing Stop으로 수익을 기대할 수 있다.

아래 맨 왼쪽 그림은 식 5)에서 μ=0.5 로 고정시키고, σ 와 L을 변화시켜가면서 E[G]의 변화를 관찰한 것이다. 변동성 (σ)이 낮을 때는 L 이 클수록 E[G]가 커진다. 즉 주가가 상승하고 (μ > 0) 변동성이 작다면 Stop Loss (L) 수준을 크게 할수록 기대 수익은 커진다. 그러나 주가가 상승해도 변동성이 크다면 L을 크게 할 때 기대 수익은 커지지만 증가폭은 작아진다. 이것은 변동성이 증가할수록 손절로 인한 청산의 기회가 많아지기 때문이다.

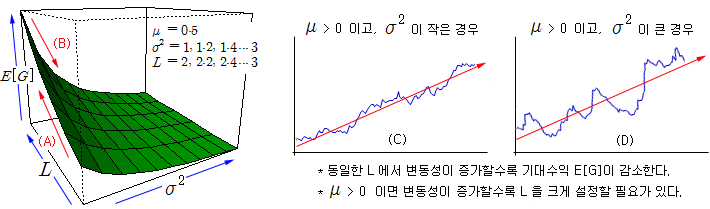
위 그림에서 E[G]를 최대로 만드는 최적의 L은 존재하지 않는다. μ > 0 라면 E[G]는 발산하는 형태이므로 L = ∞ 이고, μ < 0 이라면 L = 0 이 된다. 다른 방법으로 최적 L을 찾아보려면 효용 함수를 개입시켜서, 기대 효용이 극대화되는 L을 찾아볼 수 있다. 위험회피 형태의 효용 함수 (U)를 가정하고 기대 효용을 최대로 만드는, max. E[U(G)], L은 존재한다. ([1] 논문에서는 수치해석으로 최적 L을 찾아볼 수 있다고만 언급하고 있음). 따라서 투자 대상의 drift와 변동성만 가지고는 최적 L을 결정할 수 없고, 투자자의 위험회피 정도까지 고려해야 최적 L을 결정할 수 있다. 그러므로 절대적인 최적 L은 존재하지 않고, 투자자에 따라 주관적 (경험적)으로 결정할 수밖에 없다.

결론 :

1. 주가가 GBM을 따를 때 Trailing Stop의 기대 수익 = 0 이므로, Trailing Stop 전략만으로는 수익을 기대할 수 없다.

2. 단순 랜덤워크에서 p > q 이거나 GBM에서 μ > 0 이면, Trailing Stop 의 기대 수익은 존재한다.

3. p > q 이거나 μ > 0 조건은 진입전략으로 해결해야 한다. 기대 수익은 진입전략의 성공 여부에 달려있다. 청산전략인 Trailing Stop의 목적은 수익 창출이 아니라 Risk를 관리하기 위한 것이다.

4. 기대 수익은 주가의 변동성과 L 수준에 따라 달라진다. 일반적으로 변동성이 작으면 L의 수준을 낮추고, 변동성이 크면 L의 수준을 높게 한다.

5. Trailing Stop에서 절대적인 최적 L은 존재하지 않는다. 최적 L은 투자자의 위험회피 정도에 따라 주관적, 경험적으로 결정한다.

여기까지 Trailing Stop의 수학적 특징에 대해 살펴보았다. 다음 시간에는 Trailing Stop을 이용한 스캘핑 사례에 대해 살펴보기로 한다.

Reference :

[1] Glynn, P. W. and Iglehart, D. L. 1995. Trading securities using trailing stops. Management Science, 41, 1096-106.

[출처]15. Trailing Stop의 특성 분석|작성자아마퀀트