News & Events
기술적 분석 – Q&A (8)
이동평균의 민감도 (델타 ?)
어느 분이 이동평균과 관련된 흥미로운 질문을 주셔서 질문자님의 동의를 얻어 질문과 답변을 올려 봅니다.
질문내용 :
| 연관성을 두고 움직이는 두 값들이 있습니다. 예를 들어 종합주가지수(a)와 20일 이동평균(b)처럼 말이죠. a에 따른 b의 반응 ‘속도’를 구하려고 합니다. 제가 관련 분야 문외한이라 이렇게 표현을 했습니다만 순간 변화율이라고 해도 될 거 같습니다. 이는 흡사 기초 상품 가격에 대한 옵션의 델타와 같습니다. 그래서 델타 산출 공식을 살펴봤고 님의 블로그까지 가게 되었습니다. 표현이 맞는지 모르겠습니다만 델타는 옵션의 이론가를 구하는 과정에 사용된 d1의 표준정규분포로 구해지는데요. d1이 뭔지를 모르겠습니다. d1 산출에 사용된 파라미터들을 보면 잔존일 등 옵션에만 의미 있는 것들이 있어서 제가 원하는 b의 델타를 구하는 데에는 적용이 힘들더군요. d1의 값이 옵션의 가격과 많이 다른 값인 걸 보면 NormSDist(d1)처럼 N(b)로 될 것도 아닌 거 같습니다. b에 있어서의 d1을 구하게 되면 문제는 풀릴 거 같은데요. 혹시 제가 구하는 해답을 알고 계시면 도움을 좀 부탁드립니다. |
우선 옵션에 대한 내용을 간단히 정리해 보고, 이 논리를 이동평균 과정에 그대로 적용해 보겠습니다.
1. 기초자산 (S)과 옵션 (C)이 있음.
2. 옵션의 가격은 기초자산 가격과 관련이 있음.
3. 기초자산의 가격이 1단위 변할 때 옵션 가격의 변화량을 옵션의 델타라 함.
4. 옵션의 델타는 기초자산 가격 변화에 대한 기울기, 변화율을 의미함
5. 옵션의 델타는 근사적으로 아래와 같이 구할 수 있음.

위의 사항을 주가와 이동평균에 그대로 적용해 보기로 하겠습니다.
1. 기초자산인 주가 (P)와 이동평균 (A)이 있음.
2. 이동평균의 가격은 기초자산인 주가와 관련이 있음.
3. 주가가 1단위 변할 때 이동평균의 가격 변화량을 이동평균의 델타라 함.
4. 이동평균의 델타는 주가의 변화에 대한 기울기, 변화율을 의미함.
5. 이동평균의 델타는 근사적으로 아래와 같이 구할 수 있음.
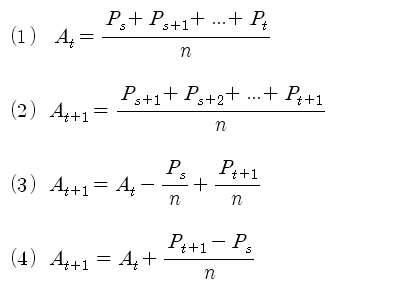
t 시점에서 n 기간의 이동평균은 식(1), 다음 시점인 t+1 시점에서 n 기간 이동평균은 식(2)로 쓸 수 있습니다. 여기서 Ps 는 시작 시점의 주가입니다 (s = start). 그러면, 식(3)과 같이, 다음 시점의 이동평균은 이전 시점의 이동평균에서 얼마큼을 더해 준 것과 같이 표현할 수 있습니다. 다음 시점의 이동평균 계산에서는 새로운 P(t+1)가 유입되고, n 기간 전의 P(s)는 빠지게 됩니다.
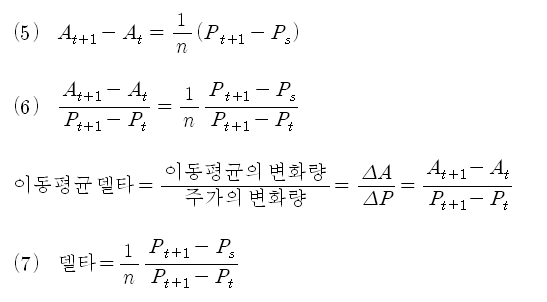
옵션과 동일한 논리를 적용하면 이동평균의 델타는 위의 식 (7)로 계산해 볼 수 있겠습니다. 아래 그림을 참조하면 위의 식을 이해하는데 도움이 될 것 같습니다.

맞는지 모르겠는데, 일단 이동평균의 민감도는 위와 같이 계산된다고 보겠습니다. 그런데 P를 x-축으로 하고, A 를 y-축으로 위의 관계를 그려보면 직선 형태가 나올 것 같습니다. 이동평균을 평활화 과정으로 보면 주가변화에 대한 반응 속도는 늦은 편이므로 델타는 (절대값) 1보다 작은 값이 나오게 되나요?
답변은 여기까지 드리도록 하겠습니다. 어디에 활용하실지는 잘 모르겠지만 흥미로운 질문이라 포스트로 답변을 드렸습니다. 추가 질문이나 의견이 있으시면 덧글로 알려 주시면, 같이 생각해 보도록 하겠습니다.
[출처]8. 이동평균의 민감도 (델타 ?)|작성자아마퀀트


