[알고리즘 트레이딩/시장미시구조] 10. Madhavan 모형 (3) – 변동성 분해

시장미시구조론 (Market Microstructure) – (10)

Madhavan 모형 (3) – 변동성 분해

이전 두 편의 포스트에서는 Madhavan의 주가모형을 설정하고 모형에 포함된 모수 (Parameter)를 추정해 보았다. 이번 시간에는 이 모형으로부터 주가의 변동성을 추정하고 시장에서 변동성에 영향을 미치는 요인들을 분석해 보기로 한다.

앞서 언급한데로, 주가 변동성에 영향을 미치는 요인은 공공정보 (Public information, News)와 시장참여자의 거래행위 자체로 나누어 볼 수 있다. 시장에 호재나 악재 같은 뉴스 (공공정보)가 발생하면 주가는 변동할 것이고, 특이한 뉴스가 없더라도 시장에서 참여자들의 전략적 충돌로 (수요와 공급의 마찰) 주가는 변동하게 된다. Madhavan 모형을 이용하면 이 요인들을 분해해 볼 수 있고, 각 요인의 정도를 계량화하여 측정해 볼 수 있다. 예를 들어, 우리나라 코스피200 지수 선물 시장에서 공공정보가 주가 변동성에 미치는 영향은 대략 30% 정도 되고, 거래행위 자체가 변동성에 미치는 영향은 약 70% 정도 된다는 식으로 각 요인의 정도를 파악해 볼 수 있다.

아래의 1) 식은 이전 시간에 설정한 주가의 모형이다. 이 식으로부터 주가의 변동성을 추출해 보자. 식 2)는 현재 주가와 이전 주가와의 차이이고, t-1 시점에서 t 시점까지의 가격 변동이 된다 (단기간의 변동성 임). 가격 변동을 시장가 주문인 xt 와 xt-1로 나타낸 것이다. 식 2)의 양변에 분산을 취하면 식 3)이 되고, 이 식을 주가의 변동성으로 사용할 수 있다.

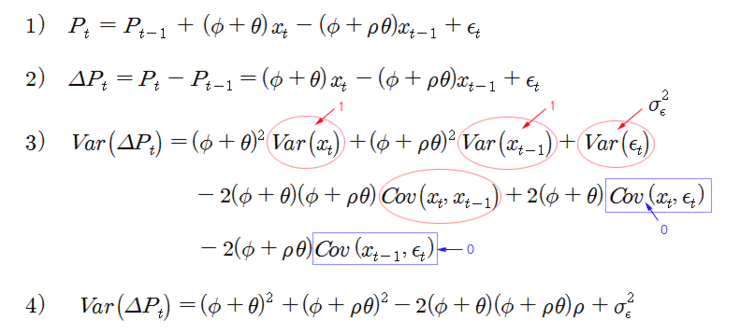
식 3)에서 xt와 xt-1은 시장가 주문의 indicator (+1 or -1)로 정의하였으므로, 그 분산은 1 이 된다. 또한, xt와 xt-1은 상관관계가 존재하므로 (시장가 주문의 연속성) 공분산은 상관계수가 된다. 그리고 xt와 잔차는 서로 독립이므로 공분산은 0 이 된다. 따라서 이 식을 정리하면 식 4)가 되고, 이 식이 바로 변동성을 분해하는 식이 된다.

식 4)의 우변을 φ 와 Θ 항을 중심으로 정리하면 식 5)가 된다. 식 5)의 첫 번째 항은 φ를 포함하고 있으므로 거래 비용이 변동성에 영향을 미치는 정도가 된다. 두 번째 항은 Θ를 포함하고 있으므로 정보의 비대칭 정도가 변동성에 영향을 미치는 정도가 된다. 세 번째 항은 φ 와 Θ를 모두 포함하고 있으므로 거래비용과 정보의 비대칭 정도의 상호작용이 변동성에 영향을 미치는 정도이다. 그리고 마지막으로 남은 잔차의 분산은 기타 항목으로 공공정보가 변동성에 영향을 미치는 정도로 해석한다.

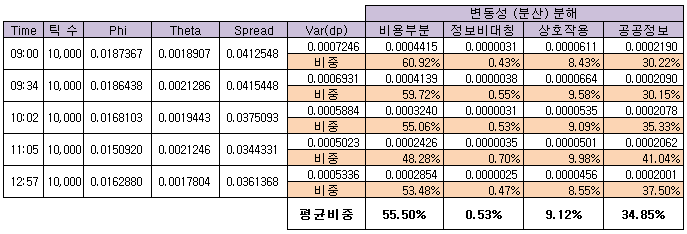
시장 데이터를 관찰하면 ρ, φ, Θ를 추정할 수 있고, 변동성을 각 요인별로 분해해 볼 수 있다. 아래 그림은 특정일의 코스피200 지수 선물에 대한 10,000 개의 체결 틱 데이터 (12:57 ~ 15:00)를 분석하여 약 2시간 동안의 변동성 (분산)을 분해해 본 그림이다.

첫 번째 틱은 12:57:44에 가격 (pt) 263.60에 시장가 매수 주문 +1개 발생한 것을 의미한다. 두 번째 틱은 3초 후에 가격 263.60에 시장가 매수 주문 +28개 발생하였고, 가격 변화 (dp = 0)는 없었다는 것을 의미한다. 두 틱 모두 시장가 매수 indicator (xt)는 +1 이다. 이 자료와 이전 시간의, Madhavan 모형 (2) – 모수추정, 논리를 적용하면 ρ, φ, Θ를 추정할 수 있다. 추정 결과 ρ=0.462, φ=0.0163, Θ=0.0018 이었다. 이 값을 이용하여 식 5)를 계산한다. 식 5)의 좌변은 dp의 분산이므로, Var[dp] = 0.000534 이다. 식 5)의 우변을 계산하면 첫 번째 항은 0.000285, 두 번째 항은 0.000002, 세 번째 항은 0.000046 이고, 마지막 항은 좌변과 우변이 같아야 하므로 0.0002 가 된다.

위의 추정 결과 식 5)의 첫 번째 항은 Var[dp] 중 53.48%를 차지한다. 이 의미는 거래비용이 주가 변동성에 미치는 영향은 약 53.48% 라는 것을 의미한다. 같은 논리로 정보의 비대칭 정도가 변동성에 미치는 영향은 약 0.47%, 이 둘의 상호작용 효과는 약 8.55%, 그리고 마지막 항인 잔차의 변동성은 기타 항목으로 공공정보의 효과로 보면 약 37.50% 가 된다. 추정 결과 거래 비용이 주가 변동성에 미치는 영향이 가장 크다는 것을 알 수 있다. 여기서 거래 비용은 Bid-Ask 스프레드를 포함한 마켓메이커의 요구 프리미엄 등으로 해석할 수 있다. 마켓메이커의 요구 프리미엄이 높을수록 단기간의 주가 변동성은 커지게 된다.

공공정보의 효과가 약 37.50% 이고, 나머지는 모두 거래 행위 자체로 인한 효과로 볼 수 있으므로 약 66.50% 가 된다. 아래 그림은 하루 데이터를 모두 계산하여 장 중의 변화를 살펴본 그림이다.

거래 비용이 변동성에 미치는 영향은 장 초반에 가장 높았고, 장 중반으로 갈수록 낮아지다가 장 후반에 약간 증가하였다. 그리고 (일일) 평균적으로 거래 행위 자체가 변동성에 미치는 영향은 약 65.15% 였고, 공공 정보의 발생이 변동성에 미치는 영향은 약 34.85% 정도였다. 이 결과는 시장미시구조론의 일반적인 결과와 잘 부합된다.

분석 결과 주가 변동성은 거래비용과 밀접한 관계가 있으므로, 변동성은 마켓메이커의 거래 행위와 밀접한 관계가 있다고 할 수 있다. 마켓메이커가 다수인 경쟁 시장에서는 마켓메이커 간의 유동성 공급 경쟁으로 인해 요구 프리미엄이 낮아지고 (완전 경쟁시장일 경우의 요구 프리미엄은 0 으로 수렴함), 변동성은 낮아진다 (유동성 증가). 반대로 마켓메이커가 적은 독점 시장의 경우 (유동성 공급량 담합으로 가정) 요구 프리미엄이 높아지고, 변동성은 증가한다 (유동성 감소). 마켓메이커가 많더라도 서로 전략적으로 공급량을 결정한다면 불완전 경쟁 (imperfect competition) 으로 볼 수 있다. 만약, 마켓메이커들이 각 주체의 합리성 보다 마켓메이커 전체의 합리성을 고려한 최적 공급량으로 경쟁한다면 (Cournot 모형 같은 게임이론을 적용하여…) 요구 프리미엄은 높아지고, 변동성도 증가한다.

여기까지 세 편의 포스트를 통해 Madhavan (1996) 모형에 대해 간략히 살펴보았다. 다음 시간부터는 시장 참여자들의 전략적 행위로 인해 주가의 변동을 설명할 수 있는 Kyle의 모형에 대해 다루어 보기로 한다.

(2015.10.28 update) Madhavan 논문의 결과보다 Θ비중이 대단히 낮게 측정되었음. Madhavan 논문 등에서는 동일 주체에 의해 분할 체결된 주문은 1개의 주문으로 간주해야 한다고 언급하고 있으나, 거래소에서 제공하는 데이터로는 이를 확인할 수 없음. 위의 결과는 직전 주문과 현재 주문의 주체가 서로 다르다는 가정하에 분석한 것임. (참고 : 지수 옵션에서 관측한 결과 : http://blog.naver.com/chunjein/220522580766)

[출처]10. Madhavan 모형 (3) – 변동성 분해|작성자아마퀀트