News & Events
[알고리즘 트레이딩/시장미시구조] 15. Market Factors의 추정 (주문의 유형별 분포)
HFT 전략 분석 (9)
Market Factors의 추정 (주문의 유형별 분포)
이번 시간에는 Market Factors 중 지정가 주문의 유입률 분포에 대해 알아본다. 지정가 주문의 유입률이란 특정 호가창 (i)에 지정가 매수/매도/취소 주문이 얼마나 빈번하게 발생하고 있는지를 분포의 형태로 표현한 것이다. 일반적으로 이 분포는 지수분포 (Exponential distribution)의 형태를 띠고 있으며, 연구 결과, 아래와 같이 표현할 수 있는 것으로 알려져 있다 (Power law). (2002, Bouchaud 외, Statistical properties of stock order books).
위 식에서 b는 지정가 주문 수량과 관계되는 추정치이고, i는 호가창의 순서 (i=1,2,3..), 그리고 a는 분포의 곡률과 관계되는 추정치이다. 이 식의 의미는 호가창이 Bid-ask spread에서 멀어질수록 (i 가 증가할수록), 지정가 주문 유입률이 낮아짐을 의미한다 (a > 1 일 때). 따라서 지정가 주문이 최우선 호가창에서 빈번하고, 이후의 호가창부터는 지수적으로 서서히 감소함을 의미한다.
시장의 종류에 따라 호가별로 지정가 주문 유입량을 측정해 보면 아래 그림과 같이 세 가지 유형으로 분류할 수 있다. A의 경우에는 최우선 호가에서 지정가 주문이 가장 높고, 호가가 시장에서 멀어질수록 지정가 주문이 서서히 감소하고 있는 모습이다. B의 경우는 최우선 호가에 지정가 주문이 밀집되어 있는 모습이고, 지정가 매수/매도 주문과 취소 주문이 매우 빈번한 시장의 유형이다. C의 경우는 지정가 주문이 전 호가에 걸쳐 비교적 균등하게 분포하고 있는 모습이다.
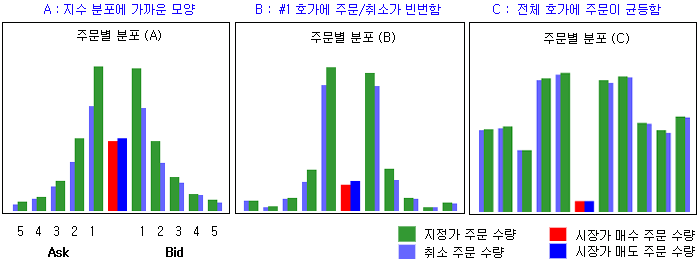
시장에 따라 주문의 분포가 다르게 나타나는 이유는 무엇인가? 당연히 투자자의 행위가 다르기 때문일 것이다. 따라서 주문의 분포를 이용하면 투자자의 행위를 파악하는 데 도움이 될 것이다. B의 경우는 가격대가 1.0 부근의 OTM 콜옵션 호가창의 모습인데, 최우선 호가창에서 투자자의 주문 경쟁이 매우 치열한 모습이다. 적은 시장가 주문을 놓고 서로 경쟁하는 모습이므로, 최우선 호가창을 대상으로 한 옵션 마켓메이커들이 많이 참여하고 있는 것으로 보인다. C의 경우는 가격대가 4.0 부근의 ATM (ATM에서 약간 ITM 쪽) 콜옵션 시장의 모습이다. #1, #2 호가에 지정가 주문이 약간 높긴 하지만 전 호가에 걸쳐 비교적 균등한 모습이다. 이것은 C시장에는 B시장에 참여한 옵션 마켓메이커들로 생각되는 세력들의 참여가 작은 것으로 생각된다.
이제, 위의 분포를 계량화하기위해 지정가 주문 유입률의 파라메터인 a, b를 추정해 보자. 분포의 모양으로 시장의 모습을 파악할 수도 있지만, 계량화 작업을 통해 수치화하면 분포의 변화를 측정하는데 매우 유용할 수 있다. 예를 들어, a, b의 변화를 관찰/기록해 두면 시간에 따라 시장이 어떤 형태로 변화하고 있는지를 쉽게 파악할 수 있고, 이에 따라 전략의 변화도 고려해 볼 수 있다.
아래 자료는 특정일의 KOSPI200 지수 선물의 주문별 수량 (09:00:00 ~ 15:00:00)을 파악한 것이다 (필자가 사용하는 HFT 시뮬레이터로 추출한 자료임).
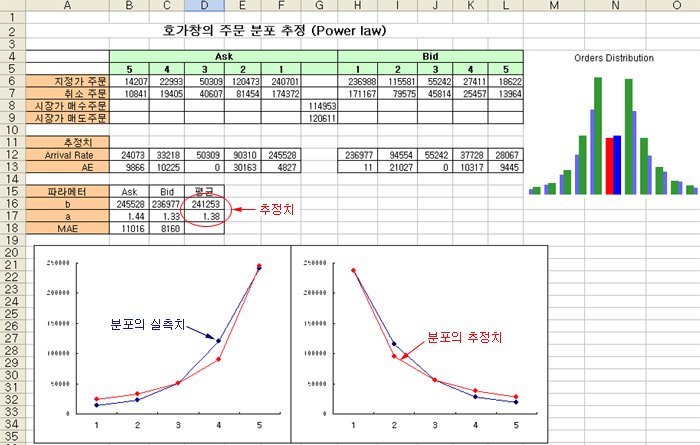
엑셀의 6번 라인의 수치는 Ask측의 호가창 별 지정가 매도주문 수량과, Bid측의 호가창 별 지정가 매수주문 수량을 측정한 것이다. 7번 라인은 각 호가창에 유입된 취소 주문 수량이고, 8번과 9번 라인은 시장가 주문 수량이다. Bid측 #1번 호가창의 경우 총 지정가 매수주문 수량은 236,988 이고, 이 중 171,167은 취소되었으며, 나머지는 주문이 체결된 것으로 보인다. 시장가 주문 수량이 큰 이유는 #2 번 이후 호가창의 체결량까지 포함된 것이기 때문이다. 지정가 주문의 취소율이 72.2% 이므로, 나머지 27.7% 만이 시장가 매도주문에 의해 체결되었을 것이다. 취소 주문율이 상당히 큰 편이다 (B와 C의 경우는 더 큼).
• 셀 B12 : = $B$16 / (B5 ^ $B$17)
•셀 B13 : = ABS(B6 – B12) — Square error는 수치가 커서, Absolute error를 사용함
•셀 B18 : = AVERAGE(B13:F13) — Absolute error의 평균 (MAE : Mean average error)
•셀 B16, B17 : 엑셀의 해찾기 (Solver)에서 MAE가 최소가 되는 k값
추정 결과 Bid/Ask의 평균 b = 241,253 과 a = 1.38 이 나왔다. b는 수량과 관계있는 수치이고, a는 지수분포 (Power law) 곡선의 곡률과 관계된 수치이다. a 값이 커질수록 곡률이 커지므로, 최우선 호가창에 주문이 집중되는 경향을 보이고, a 값이 작아질수록 곡률이 작아지므로, 주문이 호가창 별로 균등한 경향을 보이게 된다. 맨 위 그림의 B-유형의 시장은 a = 1.9 정도가 나왔다 (C-유형은 측정해보지 못함).
앞에서도 언급하였지만 각 시장 별로 주문 분포를 측정하여, 기간별로 그 변화를 관찰하여 기록해 두면, 시장 별로 전략의 변화를 고려하는데 유용할 것으로 생각된다. 이와 같이 여러 가지 Market Factor 들을 추정해보면 시장의 특성과 변화에 대해 유용한 정보를 얻을 수 있다.
