[알고리즘 트레이딩/시장미시구조] 18. 호가창과 포아송 분포

호가창 분석 (6)

호가창과 포아송 분포

주식시장의 호가창 (Limit Order Book)에서 일어나는 일련의 사건들은 (Quote Event, Order Flow 등) 통계학의 포아송 분포 (Poisson Distribution) 및 지수 분포 (Exponential Distribution)와 매우 밀접한 관계가 있다. 호가창의 사건들은 아주 짧은 시간에, 매우 복잡하게, 그리고 (거의) 연속적으로 발생하므로 통계적으로 분석할 필요가 있다.

포아송 분포는 단위 시간당 발생하는 사건의 횟수에 관심을 둔 확률분포인 반면, 지수 분포는 발생하는 사건들 사이의 시간 간격에 초점을 둔 확률분포이다. 포아송 분포와 지수 분포는 동일한 사건을 서로 다른 시각에서 관찰한 것으로 (횟수와 시간), 수학적으로는 서로 동치 관계에 있다.

포아송 분포가 적용되는 예로는, 은행 창구의 고객 대기라인, 공장의 생산라인 등이 있을 수 있고, 은행의 경우 고객들의 유입(률) 분포 등을 조사하여 창구의 최적 개수나, 은행원의 배치 문제 등을 결정하는데 활용될 수 있다.

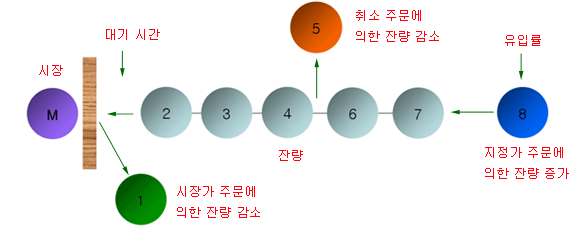
위 그림과 같이 주식시장의 호가창은 은행 창구의 대기라인과 동일한 것으로 포아송 분포를 활용하여 분석해 볼 수 있다. 고객들의 대기라인은 호가창의 잔량이 되고, 고객의 신규 유입은 지정가 주문의 유입, 은행원의 서비스는 시장가 주문으로 대입해 보면 동일한 과정이 된다. 즉, 지정가 주문, 취소 주문, 시장가 주문은 모두 포아송 분포를 따른다. 따라서 포아송 분포를 활용하면 호가창의 주문 흐름 (Order Flow)을 분석해 볼 수 있다.

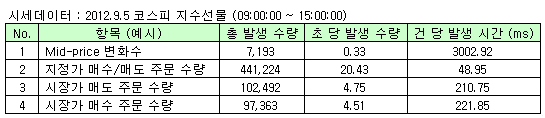
아래 그림과 같이 지수선물 호가창에서 발생한 몇몇 사건들을 이용하여 포아송 분포에 대입해 보자. 아래의 예시에서, 1일 동안 Mid-price는 총 7,193회 변화하여 평균적으로 3초당 1번씩 변하였고, 지정가 주문은 441,224 개로 초당 평균 20개 정도가 발생하였다.

포아송 분포는 아래 식과 같이 계산할 수 있다. 람다 (Lamda)는 평균 유입률 (단위 시간당 발생하는 횟수)이고, x는 확률변수, 그리고 f(x)는 발생 확률을 의미한다. 예를 들어, 평균 유입률이 초당 20회 일 때 (Lamda=20), 초당 30회가 (x=30) 발생할 확률은 f(x)가 된다 (평균이 20개라는 의미이며, 이보다 작을 때도 있고, 클 때도 있을 것이다). 엑셀에서 Lamda=4 일 때, x를 변화시켜가면서 확률을 계산하여 분포를 그려보면 아래 그림과 같이 된다.

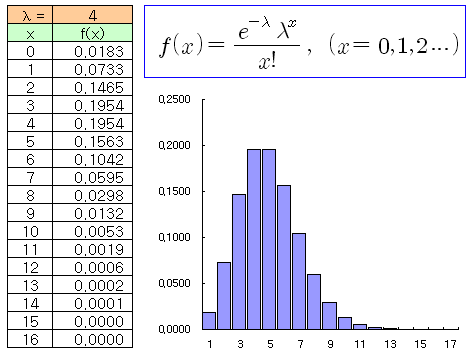
포아송 분포의 특징으로는, Lamda가 커질수록 분포의 모양이 오른쪽으로 이동하여 정규분포 같은 형태가 되며, 평균과 분산은 동일하다 (평균=분산=Lamda). 또한, 포아송 분포는 이산 확률분포이다.

이제, 호가창에 대해 포아송 분포를 적용하여 몇 가지 예제를 풀어보자.

* 2012년 9월 5일 (09:00:00~15:00:00) KOSPI200 지수선물의 호가창을 분석해 보니, 최우선 호가창에 지정가 매수 혹은 매도 주문이 총 441,224개 발생하였고, 시장가 매도 주문은 총 102,429개 발생 하였다.

Q1) 초 당 유입되는 평균 주문 수량은 얼마인가?

A1) 6시간 (21,600 초) 동안 발생한 총 개수 이므로, 지정가 주문은 초당 20개 (441,224/21,600 = 20)가 발생하였고 (유입률=20/sec), 시장가 매도 주문은 초당 4.7개 (102,429/21,600 = 4.7)가 발생하였다 (유입률=4.7/sec). 시간당 발생 횟수는 유입률 (Arrival rates) 혹은 발생강도 (Intensity)라고 한다.

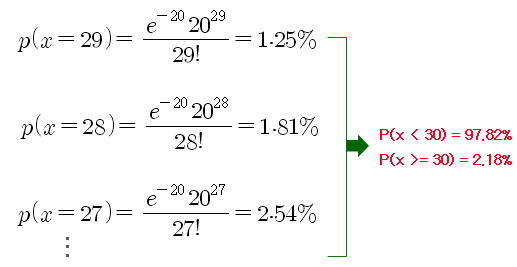
Q2) 초당 유입되는 지정가 주문 수량이 30건 이상이 될 확률은 얼마인가?

A2) 확률변수 x를 30 부터 무한히 증가시키면서 (x=30, 31, 32, …..) f(x)를 계산한 후 모두 합하면 된다 (이산 확률분포이므로 적분하지 않음). 반대로 (x=29, 28, 27, …, 0)일 때의 f(x)를 계산한 후, 100%에서 빼주면 결과는 동일하다. 결과는 아래와 같이 2.18%가 나왔다. 이 의미는 지정가 주문이 평균적으로 초당 20개가 발생하는 상황에서, 초당 30개 이상이 될 확률은 2.18% 정도가 된다는 의미이다 (확률이 희박해 보인다). 만약, 현재의 잔량이 50개라면 1초 후에 80개 이상 될 확률은 약 2.18% 정도 된다고 볼 수 있다.

Q3) 최우선 매수 호가창의 현재 잔량이 60개 이고, 내 주문이 60번째에 있다면, 내 주문이 10초 이내에 체결될 확률은 얼마인가? (단, 10초 동안 Mid-price의 변화와 취소 주문은 없다고 가정한다.)

A3) 평균적으로 10초 동안 47개의 시장가 매도 주문이 발생하는 상황에서, 10초 이내에 내 주문이 체결되려면, 10초 동안 60개 이상의 시장가 매도 주문이 발생해야 한다. 그러므로 10초 동안 60개 이상의 시장가 매도 주문이 발생할 확률을 계산하면 된다. 결과는 아래와 같이 3.81% 가 나왔다 (이것도 매우 희박한 확률이다).

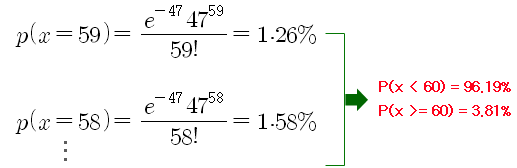
위의 예제와 같이 포아송 분포를 활용하면 호가창의 사건들을 통계적으로 계산해 볼 수 있다. 다음 시간에는 포아송 분포의 시뮬레이션을 디자인 해 보고, 시뮬레이션을 통해 위 예제의 결과를 다시 확인해 보기로 한다.

[출처]18. 호가창과 포아송 분포|작성자아마퀀트