[알고리즘 트레이딩/시장미시구조] 21. 호가창과 지수 분포

호가창 분석 (9)

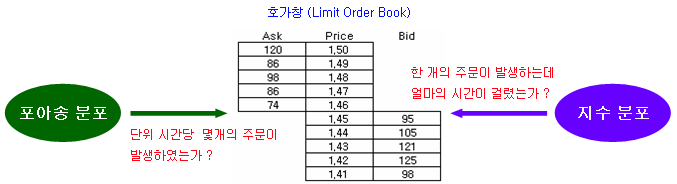
호가창과 지수분포

이전 시간에 살펴본 포아송 분포는 단위 시간당 발생하는 주문의 개수 (사건 발생 횟수)에 관심을 둔 분포이다. 반면에 한 개의 주문이 발생하는데 걸리는 시간에 관심을 두면 지수 분포 (Exponential Distribution)가 된다. 즉, 포아송 분포의 확률변수는 (확률분포의 x-축) 주문 발생 횟수가 되고, 지수 분포의 확률변수는 주문이 발생하는데 걸리는 시간이 된다. 따라서 포아송 분포와 지수 분포는 어떤 사건에 대해 바라보는 관점만 다를 뿐 동일한 것이다 (수학적으로 상호 동치의 관계에 있음). 그리고 포아송 분포의 확률변수는 양의 정수 (발생 개수)이므로 이산확률분포이고, 지수 분포의 확률변수는 양의 실수 (임의의 시간)이므로 연속확률분포이다.

아래 그림과 같이 예를 들어보자. 첫 번째 주문이 발생하고, 0.25초 후에 또 하나의 주문이 발생하였다. 0.15초 후에 또 다른 주문이 발생하였고, 이후에도 불규칙한 시간 간격으로 주문이 지속적으로 발생하고 있는 상황이다. 단위시간을 1초로 한 경우, 처음 1초 동안에 발생한 주문은 6건이 된다. 다음 1초 동안에 발생한 주문은 5건이 될 수도 있고, 6건이 될 수도 있고, 혹은 10건이 될 수도 있다. 이렇게 개수에 관심을 둔 분포가 포아송 분포이다.

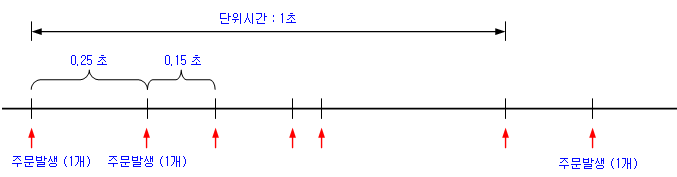
이번에는 주문발생 사이의 시간에 대해 살펴보자. 최초 주문 발생 후 다음 주문이 발생할 때 까지는 0.25초가 걸렸고, 그 다음은 0.15초가 걸렸다. 다음 주문은 0.2초가 걸릴 수도 있고, 0.5초가 걸릴 수도 있다. 이 시간들도 어떤 분포를 형성하게 되는데, 이것이 바로 지수 분포가 된다.

지수 분포는 아래의 식과 같이, 포아송 분포로부터 추출해 볼 수 있다. 식 1)은 단위 시간당 발생하는 사건의 포아송 분포이고, 식 2)는 t 시간 동안의 포아송 분포이다. 위 그림에서 사건 발생 사이의 t 시간 내에는 사건이 전혀 발생하지 않으므로 t 시간 이내의 사건발생의 개수 = 0 이다. 따라서 식 2)에 x = 0를 대입하면 식 3)을 얻을 수 있다. 그러면 (t를 포함하여) t 시간 이내에 1 개 이상의 사건이 발생할 확률은 식 4)로 표현할 수 있고, 이 식은 CDF가 된다. 식 4)를 PDF인 확률밀도함수로 나타내면 식 5)를 얻을 수 있는데, 이것이 바로 지수 분포의 확률밀도함수가 된다. 식 4)와 5)의 변환은 식 6)의 과정을 통해 확인해 볼 수 있다.

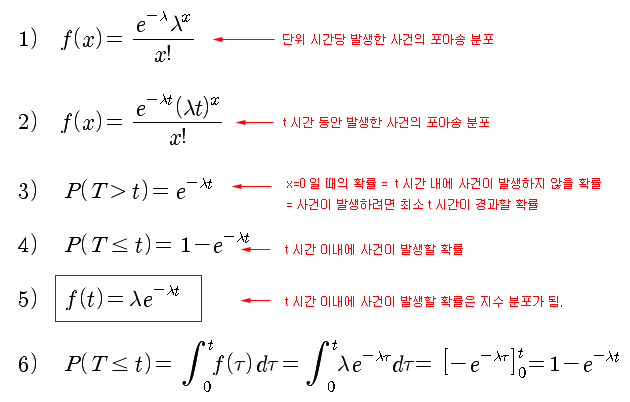
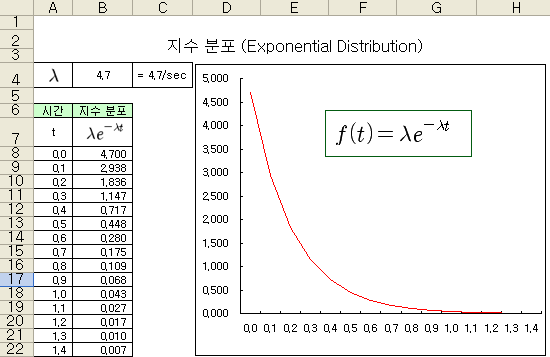
식 5) 지수 분포의 Lamda 도 포아송 분포와 마찬가지로, 사건의 발생율 (발생 강도, Intensity, Arrival rate 로도 쓰임)을 의미하고, 시간당 발생한 사건의 개수로 표현된다 (단위가 1/시간 임). 만약 시장가 주문이 초당 4.7개 유입된다면, Lamda = 4.7/sec 가 된다. 시간을 0 ~ 1.4 초로 변화 시켜가면서 Lamda = 4.7인 경우의 지수 분포를 그려보면 아래 그림과 같이 된다.

이제 실례를 통해 지수 분포를 이용한 확률을 계산해 보자.

예제) 어느 날 (09:00:00 ~ 15:00:00) KOSPI200 지수 선물의 시세 데이터를 이용하여 호가창을 분석해 보았더니, 1일 동안 Mid-price가 총 7,193번 변화 하였다.

Q1) Mid-price가 1번 변하는 데 걸린 평균 시간은 얼마인가?

– 6시간 (21,600 초) 동안 7,193번 변했으므로, 평균적으로 1번 변하는데 걸린 시간은  (21,600/7,193) 약 3초 이다. 평균 대기 시간 = 3 초

Q2) 단위 시간당 Mid-price의 변화율은 얼마인가?

– 3초에 1번 변화하였으므로, 초 당 1/3 번 변하였다. 변화율 = 0.33 / sec  (λ = 0.33 /sec)

Q3) 특정 시점에 최우선 호가창에 지정가 주문을 넣었다. 지금부터 5초 이내에 Mid-price가 바뀔 확률은 얼마인가?

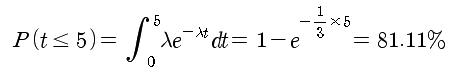
평균적으로 Mid-price가 3초에 1번 변하는데, 5초 이내에 변할 확률은 81.11%로 비교적 높게 나왔다. 평균적으로 3초에 1번 변한다는 의미는, 실제로는 1초에 1번 변할 수도 있고, 10초에 1번 변할 수도 있는데, 이것을 전부 평균하면 3초에 1번이라는 의미이다. 이런 상황에서 5초 이내에 변할 확률이 약 81%이고, 5초 이상일 확률은 19% 라는 의미가 된다.

위 예제에서 보듯이 지수 분포는 연속확률분포이므로 적분식을 사용하여 쉽게 확률을 계산할 수 있다 (포아송 분포에 비해). 또한, 지수 분포는 t에 대한 식으로 쉽게 표현할 수 있으므로 포아송 분포보다 훨씬 쉽게 시뮬레이션을 만들 수 있다. 다음 시간에는 지수 분포의 시뮬레이션 방법에 대해 알아보기로 한다.

[출처]21. 호가창과 지수 분포|작성자아마퀀트