[알고리즘 트레이딩/시장미시구조] 25. PIN 모형 (1) – 모형의 설정

시장미시구조론 (Market Microstructure) – (25)

PIN 모형 (1) – 모형의 설정

그 동안 여러 편의 포스트를 통해 Kyle의 모형에 대해 살펴보았다. Kyle의 모형에는 정보기반 거래자 (Informed Trader), 유동성 거래자 (Noise Trader), 그리고 시장조성자 (Market Maker)가 시장에 참여한다. 그리고 각각이 추구하는 최적의 전략들이 경쟁 (충돌)하면서 시장은 균형 상태에 이른다. Kyle의 모형은 추상적이긴 하지만 몇 가지 가정을 통해 시장의 모습을 잘 그려내고 있다.

시장미시구조론 (Market Microstructure)의 대다수 이론들은 정보기반 거래자에 관심을 많이 갖는다. 이것은 주가가 정보와 매우 밀접한 관계가 있기 때문이다. 그럼 시장에서 실제 데이터를 관측하여 얼마나 많은 정보기반 거래자가 참여하고 있는지 추정할 방법은 없을까?

David Easley (외 3명)는 1996년 정보기반 거래자의 시장 참여율을 추정할 수 있는 PIN (Probability of Informed Trading) 모형을 발표하였다 [1]. PIN 모형은 단위 시간당 발생한 거래 (매수 수량, 매도 수량) 데이터를 이용하여 얼마나 많은 정보가 시장으로 유입되고 있는가를 추정하여 정보기반 거래자의 참여 정도를 계량화한다. 정보기반 거래자가 보유한 정보는 그들의 거래 행위에 의해 시장에 노출된다. 거래 행위로 거래량이 발생하고 매수와 매도 거래량의 불균형 정도에 따라 변동성이 발생하고 주가는 변화한다. 따라서 매수, 매도 거래량의 불균형 정도를 측정하면 정보기반 거래자의 참여 비중을 추정해 볼 수 있다.

PIN 모형의 설정

PIN 모형은 아래 그림과 같이 설정한다. 현재 시장에는 정보기반 거래자의 정보가 있을 가능성도 있고, 없을 가능성도 있다. 여기서 정보는 News와 같이 모든 거래자가 알고 있는 정보가 아니라, 정보기반 거래자만 알고 있는 것을 의미한다. 정보가 있을 확률은 α 로 표시한다. 정보가 없을 확률은 1-α 가 된다. 만약, 정보가 없다면 (α = 0), 시장에는 노이즈 거래자들만 거래하는 상태가 된다. 시장에 정보는 존재하지 않고 주가는 단순 랜덤 워크 (Random walk)를 따라 움직인다 (주가가 횡보 상태가 되는 것이 아님). 시장에 정보가 없으므로 노이즈 거래자들에 의해 발생한 거래 변동성만 존재한다. 이 변동성은 비교적 일정하므로 (constant) 주가는 랜덤 워크를 따른다 (주가 수익률 시계열에 이분산성이 나타나지 않음).

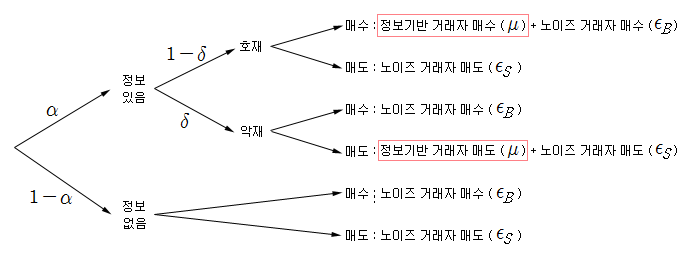
만약, 정보기반 거래자의 정보가 존재한다면 (α > 0), 이 정보가 호재성 정보일 수도 있고, 악재성 정보일 수도 있다. 호재성 정보일 확률은 1-δ, 악재성 정보일 확률은 δ 로 표시한다. 호재성 정보라면 정보기반 거래자는 매수 주문을 쏟아낼 것이고, 악재성 정보라면 매도 주문을 퍼부을 것이다. 정보가 호재성이든, 악재성이든 노이즈 거래자 (비정보 기반 거래자) 들은 매수와 매도를 꾸준히 할 것이다 (정보를 모르므로…).

정보기반 거래자가 정보를 가지고 있으면 (특정 기업에 대한 정보나, 시장 전반에 관한 정보 등), 주가는 단순 랜덤워크를 따르지 않는다. 이것은 거래로 인한 변동성 이외에 정보로 인한 변동성이 추가로 발생하기 때문이다 (Madhavan 모형 참조). 즉, 주가는 이분산성을 갖는 랜덤워크 모형을 따르게 된다.

정보기반 거래자의 거래 강도 (Intensity)는 μ 로 표시한다 (매수든 매도든 상관없음). 그리고 노이즈 거래자의 매수 (Buy) 강도와 매도 (Sell) 강도는 각각 εB 와 εS 로 표시한다. 여기서 강도는 단위 시간당 발생하는 매수, 혹은 매도 거래량을 의미한다. 예를 들어 εB 는 1시간 당 발생하는 노이즈 거래자의 매수 수량을 의미한다. 단위 시간은 시간 (Hourly) 단위가 될 수도 있고, 일 (Daily) 단위가 될 수도 있다. 혹은 더 짧게 분 단위가 될 수도 있다. 각 거래자들의 주문 수량은 포아송 분포를 따르기 때문에 거래 수량 대신 거래 강도로 표시한다 (포아송 분포 참조).

이 모형을 이용하면 시장에 발생한 총 매수 강도와 총 매도 강도를 추정할 수 있고, 총 거래 강도 대비 정보기반 거래자의 거래 강도를 이용하면 정보기반 거래자의 참여 정도를 추정할 수 있다. 식 1)은 시장에서 관측되는 총 매수 강도를 조건부 확률을 이용하여 표현한 것이다. 위 그림에서 매수가 발생하는 경우는 총 3가지이므로, 이들을 모두 더하면 총 매수 강도가 된다. 동일한 방법으로 총 매도 강도는 식 2)로 표현할 수 있고, 식 3)의 총 거래 강도는 매수 강도와 매도 강도를 합친 것이다. 시장에서 단위 시간당 총 매수 수량과 매도 수량을 관찰할 수 있으므로, 매수/매도 강도를 측정할 수 있다. 측정된 매수/매도 강도를 이용하면 우변의 각 파라메터 (α, δ, μ, ε) 들을 추정할 수 있다.

식 4)는 정보기반 거래자의 거래 강도를 표현한 것이다. 정보기반 거래자는 정보가 존재하는 경우에만 거래하므로 식 4)로 표현할 수 있다. 식 3)과 식 4)를 이용하면 정보기반 거래자의 참여 비중인 PIN은 식 5)로 표현할 수 있다. 간단히 총 거래 강도 중 정보기반 거래자의 거래 강도를 비율로 나타내면 된다. 원 논문 [1]에서는 조건부 확률을 이용하여 체계적으로 식 5)를 도출하였으나, 여기서는 직관적으로 식 5)를 이해하기로 한다.

위 식에서 α = 0 이라면, 즉, 정보가 없다면, 매수 강도 = εB, 매도 강도 = εS 가 되고, 두 강도가 정규분포를 따른다면 주가는 단순 랜덤워크를 따른다. α = δ = 1/2 이라면, 즉, 모든 확률이 50:50 이라면, 매수 강도 = μ/4 + εB, 매도 강도 = μ/4 + εS 가 된다. εB와 εS가 대칭이라면 매수/매도 강도도 대칭이 되어, 이 경우도 단순 랜덤워크를 따르게 된다. 만약, α = 1, δ = 0 이라면, 정보가 존재하고 호재성 정보라면, 매수 강도 = αμ + εB, 매도 강도 = εS 가 되어 매수/매도 강도가 비대칭이 되어 시장에 불균형이 발생하고, 변동성 (이분산성)이 발생한다.

여기까지 간단히 PIN 모형을 설정해 보았다. 이 모형을 완성하려면 시장에서 관측한 매수/매도 강도를 가지고 각 파라메터를 구하여, PIN을 추정해야 하는데, 식은 2개이고 파라메터는 5개 이므로 직접 계산은 불가하다. 따라서 가장 그럴듯한 확률이 되도록 5개의 파라메터를 추정해야 한다. 다음 시간에는 5개의 파라메터를 추정하기 위한 우도 함수 (Likelihood)를 설정해 보기로 한다.

참고자료:

[1] David Easley, Nicholas M. Keifer, Maureen O’Hara, Joseph B. Paperman, 1996, Liquidity, Information, and Infrequently Traded Stocks.

[출처]25. PIN 모형 (1) – 모형의 설정|작성자아마퀀트