[알고리즘 트레이딩/시장미시구조] 27. PIN 모형 (3) – 우도 함수의 변형

시장미시구조론 (Market Microstructure) – (27)

PIN 모형 (3) – 우도 함수의 변형

이전 포스트에서 설정한 PIN 모형의 우도 함수 (Likelihood)를 실제로 계산하려면 컴퓨터에서 연산이 가능한 형태로 변환해야 한다. 식 1)에서 B와 S 는 단위 시간당 발생한 매수/매도 거래량으로, 거래량이 수만, 혹은 수십만 정도가 되면 연산이 곤란하다 (단위 시간은 일일 단위가 될 수도 있음). 물론, 컴퓨터 프로그래밍 기법에도 대단히 큰 수나, 대단히 작은 수를 처리하는 방법이 있겠지만, 그 것 보다는 수학적으로 변형하는 것이 훨씬 유용할 것이다.

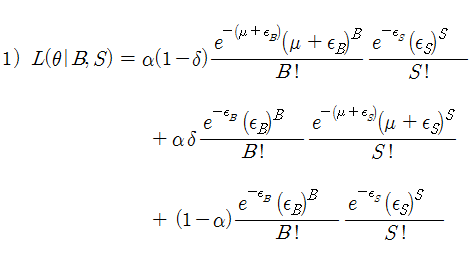
2005년 Easley, Hvidkjaer 그리고 O’Hara 는 식 1)을 다음과 같이 변형하였다 (EHO 방식이라 하자). 우선, 식 1)을 아래와 같이 변형한다.

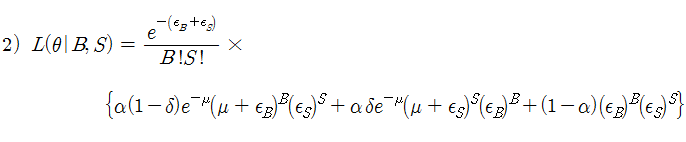
식 2)는 특정 구간의 우도 함수이므로, 전 구간의 우도 함수를 계산하려면 식 2)를 모두 곱해주어야 한다 (결합확률분포). 식 2)를 모두 곱한 수식은 매우 복잡하므로, 식2)를 모두 곱한 식에 로그를 취하여 로그 우도 함수를 만든다. 로그 우도 함수가 최대가 되면, 우도 함수도 최대가 되므로, 편의상 식 3)과 같이 로그 우도 함수를 만들어 사용한다. 즉, 식 2)를 모두 곱한 후, 양변에 로그를 취한다. 그리고 1/B!S! 은 파라메터와 무관한 상수이므로 제거해도 된다 (제거해도 우도 함수가 최대가 되는 조건은 불변임).

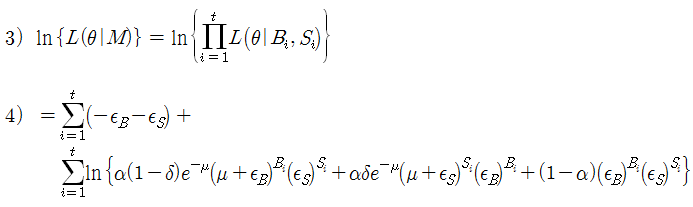
식 5)와 같이 xB, xS 변수를 치환하여, xB와 xS를 식 4)에 대입하면 식 6)을 얻을 수 있다. 그리고 임의의 Mi를 도입하여 식 6)에다 한번 더하고 한번 빼는 방식으로 Mi를 끼워 넣어 식 7)을 만든다. 이것은 승수인 B와 S의 규모를 줄이기 위해, 승수가 B-Mi, S-Mi 가 되도록 변형하기 위함이다. 여기서 Mi는 임의의 값으로, 승수가 되도록 작게 되는 값으로 설정한다.

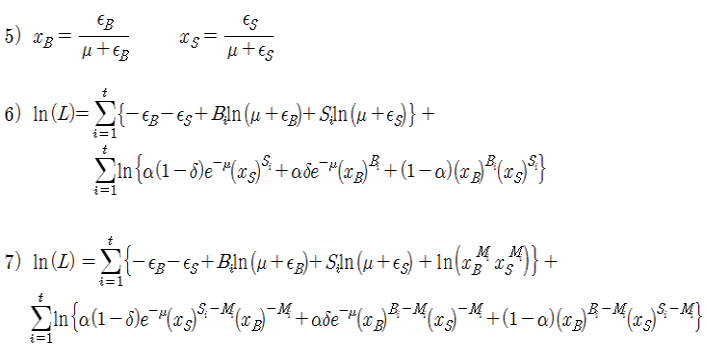
식 7)을 변형하면 최종적으로 식 8)을 얻을 수 있다. EHO 방식에서 Mi는 아래와 같이 정의한다.

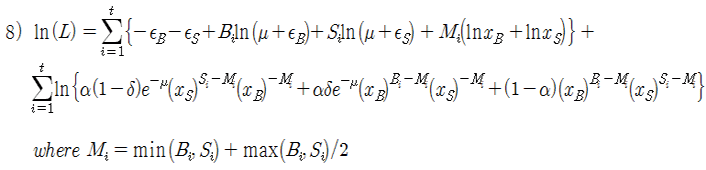
식 8)은 컴퓨터로 계산이 가능한 표현으로, 2002년 Easley, Hvidkjaer 와 O’Hara가 제안한 방식이다. 그러나 이 식도 B와 S가 커질수록 계산 결과가 부정확해질 수 있다. 이 식으로 여러 종목에 대해 PIN을 추정하다 보면, 거래량이 매우 컸던 날들은 우도 함수가 수렴하지 못하는 현상이 가끔 발생하곤 한다 (필자가 실제로 경험했음).

2011년 Lin, W.W 와 W.C Ke 는 EHO 방식의 부정확성을 개선하기 위해 우도 함수를 아래와 같이 변형하였다 (유도 과정은 생략. 이 방식을 LK 방식이라 하자).

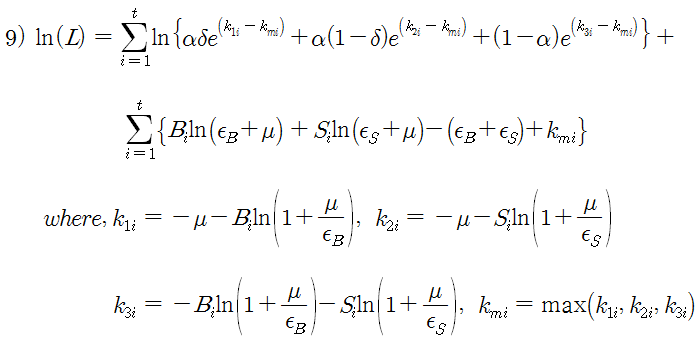
식 9)는 LK 방식의 우도 함수이다. B와 S가 아무리 커져도 안정된 계산 결과가 나온다. 향후 포스트에서 삼성전자 종목에 대해 실제 PIN을 추정해 볼 예정인데, 그 때 LK 방식을 적용하기로 한다. 우리의 목표를 다시 한번 정리해보면, 실제 시장 데이터를 관측해서 식 9)가 최대가 되는 파라메터 (α, δ, μ, ε)를 추정하고, 시장에 정보기반 거래자가 어느 정도 참여하고 있는가를 추정해 보는 것이다.

여기까지 PIN 모형을 설정하고, 우도 함수의 기본형을 만들고, 계산이 가능한 형태로 변형한 것까지 알아보았다. 그러나 최종 결과를 얻기 위해서는 아직 해결해야할 문제가 남아있다. 바로 파라메터의 초기값 설정 문제이다. 수치해석에서 초기값에 따라 추정 결과가 다르게 나타날 수 있으므로, 초기값을 합리적으로 설정하는 것은 매우 중요한 일이다. 이 부분에 대해서는 다음 포스트에서 자세히 살펴보기로 한다.

[출처]27. PIN 모형 (3) – 우도 함수의 변형|작성자아마퀀트