[알고리즘 트레이딩/시장미시구조] 28. PIN 모형 (4) – 우도 함수의 초깃값

시장미시구조론 (Market Microstructure) – (28)

PIN 모형 (4) – 우도 함수의 초깃값

이전 포스트에서 살펴본, Lin & Ke (2011)의 우도 함수를 최대로 만드는 파라메터 (α, δ, μ, ε)들은 수치해석으로 추정해야 하고, 수치해석을 위해서는 적절한 초깃값이 필요하다. 우도 함수의 극대점이 포물선처럼 한 군데만 있다면, 초깃값을 임의로 설정해도 되지만, 극대점이 여러 개 존재한다면 초깃값에 따라 수치해석의 결과가 달라질 수 있다.

아래 그림은 PIN 파라메터들과 우도함수의 관계를 임의로 그려본 것이다. 실제 관계는 6차원 공간에서 생각해야 하므로, 어떤 형태일지 상상할 수는 없다. 아래 그림은 실제 관계가 2차원 공간으로 투영된 것으로 생각하고, 여러 곳에 변곡점이 있다고 상상해 보자.

파라메터의 초깃값을 (1)로 설정한 후 우도함수의 극대점을 찾아가면, 지역적 극대점 (Local Max.)인 (A)를 찾아가고, 초깃값 (4)에서 시작하면 (D)를 찾아간다. 우리의 목표는 전역적 극대점 (Global Max.)인 (B)를 찾는 것이다.

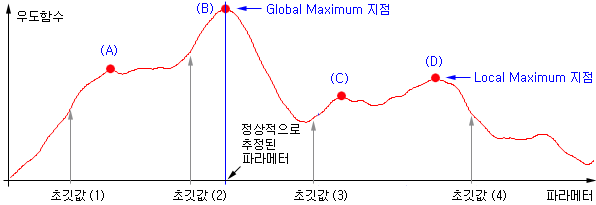
전역적 극대점을 찾으려면 서로 다른 여러 지점에서 (가능한 많은 지점에서) 시작해서 가장 큰 극대점을 찾아야 한다. 즉, 초깃값을 여러 개 설정하여, 가능한 모든 극대점들을 찾는 것이다. 전 구간에서 모든 극대점을 찾으려면, 각 파라메터의 가능한 모든 범위에 대해 계산해야 한다.

파라메터의 구간이 제한되어 있는 경우 (Bounded)는 전체 범위를 검색할 수 있다. α와 δ는 0 ~ 1 사이의 값이므로 이 범위 내에서 초깃값을 여러 개 설정하면 된다. 전체 구간을 설정하려면, α (or δ) = 0.1, 0.2, 0.3 … 0.9 정도로 설정하면 된다. 그러나 구간이 제한되지 않은 경우 (Unbounded)는 전체 범위를 적용하기 어렵다. μ와 ε의 범위는 0 ~ ∞ 이므로, 이 구간을 전부 커버하려면 초깃값을 무한히 설정해야 한다.

이 문제를 해결하기위해 Yan & Zhang (2012)은 아래와 같은 방법을 소개하였다. 파라메터들의 몇 가지 관계를 이용하면, 각 파라메터의 범위를 제한할 수 있다 (Bounded).

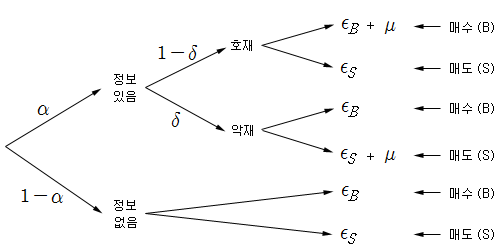
위 그림은 매수 주문 (B)과 매도 주문 (S)이 발생하는 경우를 그린 것이다. 이 그림을 이용하면 매수 주문의 기댓값 (E(B) : 평균 매수 수량)과 매도 주문의 기댓값 (E(S) : 평균 매도 수량)을 식 1)과 2)로 나타낼 수 있다. E(B)와 E(S)는 시장 데이터로부터 관측할 수 있는 값이다 (상수임).

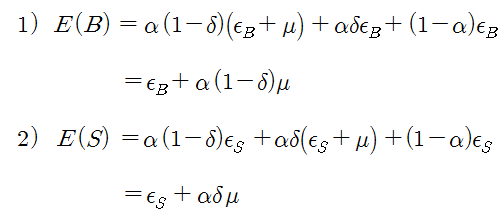
식 1)에서 우변의 값은 0보다 크고, α(1-δ)μ 도 0 보다 크므로, εB 는 E(B)보다 작거나 같아야 한다. 식 3). 그러면 εB 는 식 4)처럼 범위가 제한된 식으로 만들 수 있다. 즉, 가능한 εB의 범위는 εB = 0.1*E(B), 0.2*E(B), … 0.9*E(B)로 설정하면 된다.

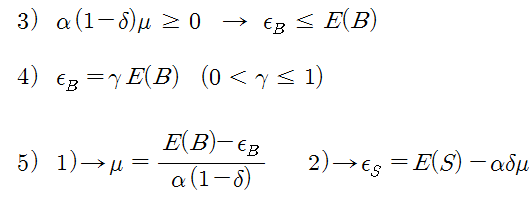
다음으로 식 1)과 2)를 이용하면 식 5)와 같이 μ와 εS를 계산할 수 있다. 식 5)의 우변의 각 변수들은 모두 범위가 제한된 변수들이므로 μ와 εS도 범위가 한정된다. 여기까지의 관계를 이용하면 각 파라메터들의 가능한 초깃값 조합은 식 6)처럼 설정해 볼 수 있다.

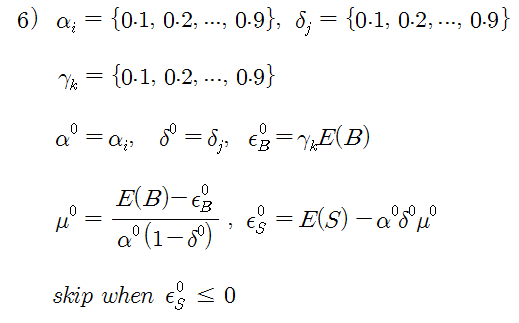
식 6)의 경우 초깃값 조합의 개수는 9 * 9 * 9 = 729개이다. 즉, 729개 지점에서 출발하여 가능한 모든 극대점을 찾아내고, 이 중 가장 큰 극대점을 찾는 것이다. 이 방법을 이용하면 꽤 정확히 Global Max. 지점을 찾을 수 있다 (α,δ,γ 값이 연속이 아니기 때문에 100% 확실한 것은 아님). 조합이 너무 많다고 생각되면, α,δ,γ의 범위를 0.1, 0.3, 0.5 … 0.9로 설정할 수도 있다. 그러면 조합의 개수는 125개로 줄어든다. 이 방법은 정확하긴 하지만  추정 시간이 오래 걸린다는 단점이 있다.

추정 시간을 단축하는 알고리즘은 나중에 논의하기로 하고, 우선, 여기까지의 내용만으로 실제 시장데이터를 분석해서 각 파라메터를 추정해 보기로 한다. 추정 방식을 다시 정리해 보면, Lin & Ke (2011)의 우도 함수와 Yan & Zhang (2012) 의 초깃값을 이용하여 Easley & Kiefer & O’Hara (1996)의 PIN 파라메터를 추정하는 것이다. 실제 추정 결과는 다음 포스트에서 살펴보기로 한다.

[출처]28. PIN 모형 (4) – 우도 함수의 초깃값 |작성자아마퀀트