News & Events
[알고리즘 트레이딩/시장미시구조] 35. PIN 모형 (11) – PIN과 CPIN의 결과 비교
시장미시구조론 (Market Microstructure) – (35)
PIN 모형 (11) – PIN과 CPIN의 결과 비교
이번 시간에는 PIN과 CPIN의 추정 결과를 비교해 보기로 한다. PIN은 Lin & Ke 우도함수를 이용하여 MLE로 추정한 결과이고, CPIN은 데이터 사이언스의 클러스터링 (Clustering) 기법을 이용하여 추정한 결과이다.
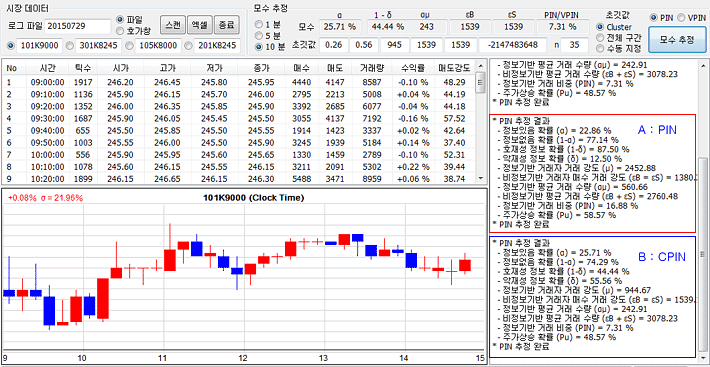
아래 그림은 2015.7.29.일 코스피200 선물 (9월물)의 10분봉 데이터이다 (틱 데이터는 XingAPI를 이용하여 수집하였음). PIN 추정 결과는 16.88% 이고, CPIN 추정 결과는 7.31% 이다 (과거 약 30% 정도에 비해 상당히 낮아진 것임). 두 결과가 2배 이상 차이가 났다. 사적 정보가 존재할 확률은 22.86% 와 25.71%로 비슷하게 측정되었으나, 호재성 정보일 가능성은 87.50% 와 44.44% 로 큰 차이가 났다.
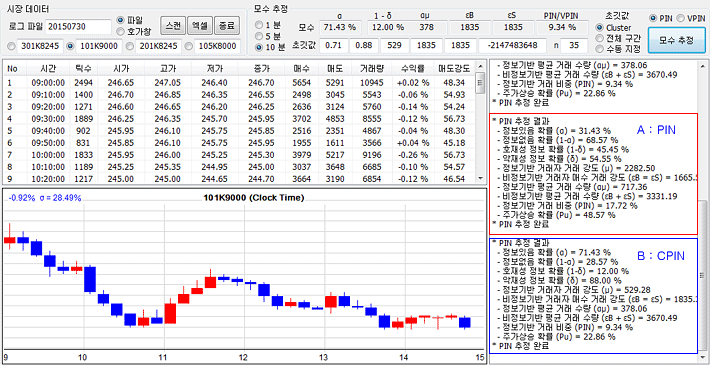
아래 그림은 2015.7.30. 일의 10분봉 데이터이다. PIN 추정 결과는 17.72% 이고, CPIN 추정 결과는 7.31% 이다. 이 결과에도 큰 차이가 있다. 사적 정보가 존재할 확률도 31.43% 와 71.43%로 차이가 크게 나타났으며, 호재성 정보일 가능성도 45.45% 와 12.00% 로 큰 차이가 났다.
이틀간의 결과를 요약하면 아래와 같다.
왜 이런 차이가 발생하는 것이고, 어느 결과를 신뢰할 것인가? PIN 모형은 매수와 매도 사건의 거래 메카니즘을 합리적으로 해석하여 (포아송 분포 및 우도함수) 추정한 결과이다. 그러나 CPIN은 일반적인 데이터 분류 기법을 사용했기 때문에 PIN 이라는 특수한 상황에 대한 고려가 부족한 면이 있다. 만약, PIN모형에 적합한 분류기를 새로 고안해서 추정한다면 PIN과 유사한 결과를 얻을 수도 있을 것이다. 직관적으로 해석해 보아도 PIN 결과가 더 타당해 보인다.
그런데, CPIN은 자체적으로는 큰 의미가 없을지 몰라도, PIN과 결합해서 사용하면 매우 유용하다. CPIN의 저자도 논문에 언급했듯이, CPIN의 추정치를 PIN의 초깃값으로 사용할 수 있다. PIN 모형은 전 구간을 검색하여 MLE를 추정하기 때문에 계산 속도가 매우 늦다. 그러나 CPIN의 결과를 초깃값으로 사용하면 MLE를 한 번만 계산하면 되기 때문에 MLE 추정 속도를 상당히 높일 수 있다. 실제 위의 데이터로 CPIN의 결과를 초깃값으로 MLE를 추정하면, PIN의 결과와 동일하게 나오면서, 추정 속도는 대단히 빨라진다.
그동안 PIN 모형에 대해 언급해 왔다. PIN 모형에서 가장 중요한 자료는 매수 체결량과 매도 체결량이다. 따라서 매수, 매도 체결량의 정의는 무엇이고, 어떻게 측정할 것인가? 가가 중요한 이슈가 될 수 있다. 이 부분에 대해서는 다음 시간에 알아보기로 한다.
