[알고리즘 트레이딩/시장미시구조] 38. VPIN 모형

시장미시구조론 (Market Microstructure) – (38)
VPIN 모형

지난 시간에 살펴 본 바와 같이 동일한 거래량을 갖는 캔들을 만들면 근사적으로 PIN을 추정해 볼 수 있다. 이렇게 추정된 PIN을 Volume-Synchronized PIN (VPIN)이라 한다. VPIN 모형은 David Easley (외 2명)의 2012년 논문인 “Flow Toxicity and Liquidity in a High Frequency World”에 자세히 소개되어 있다.

​

PIN 모형은 포아송 분포로 우도함수를 만들고 수치해석으로 MLE를 찾아 모형의 모수들을 추정한 후 PIN 값을 계산한다. 말도 어렵고 과정도 대단히 복잡하다. 그러나 VPIN 모형은 거래량이 동일한 캔들만 만들면 아주 쉽게 PIN을 추정할 수 있다. 우도함수도 필요 없고, 수치해석도 필요 없다. 따라서 추정 속도가 대단히 빠르다.

​

거래량이 동일한 캔들은 아래 그림과 같이 만들면 된다. 동일한 크기의 비어있는 Bucket을 만들어 놓고 (Volume bucket 이라 함), 체결 틱이 발생할 때 마다 체결 수량 (거래량)을 왼쪽 Bucket부터 채워 나가면 된다. 한 Bucket에 채우고 남은 체결 수량은 다음 Bucket에 넣는다. 체결 수량을 쪼갤 수 있는 것은, 한 번에 +8개의 매수 체결이 발생한 사건과,  +1개의 매수 체결이 동시에 8번 발생한 것과 동일하다는 것을 전제로 한다.

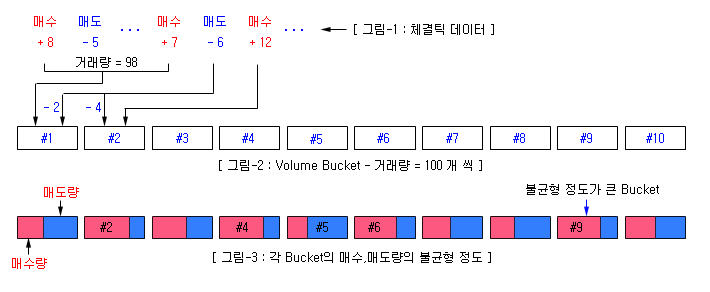
위 그림은 거래량을 100개씩 갖는 Volume Bucket을 만드는 과정이다. 처음에 8개의 매수 체결이 발생하면 8개를 첫 번째 Bucket에 넣고, 두 번째 5개의 매도 체결도 첫 번째 Bucket에 넣는다. 이런 식으로 첫 번째 Bucket을 채워나가다가 첫 번째 Bucket의 거래량이 98개가 되었을 때 6개의 매도 체결이 발생했다면 거래량 6개는 첫 번째 Bucket에 넣을 수 없으므로, 이 중 2개만 첫 번째 Bucket에 넣고 (거래량 = 100), 나머지 4개는 두 번째 Bucket에 넣는다. 이런 식으로 각 Bucket이 채워지면 [그림-3]과 같이 각 Bucket에는 매수 수량과, 매도 수량이 쌓이게 된다 (매수 수량 + 매도 수량 = 100).

[그림-3]의 각 Bucket에는 매수 수량과 매도 수량이 분포를 이루고 있는데, 어떤 Bucket들은 매수와 매도가 균형을 이루고 있고, 어떤 Bucket들은 균형을 이루지 못하고 한 쪽으로 치우쳐 있다 (#2, #4, #5, #6, #9). 매수와 매도가 균형을 이룬 Bucket들은 정보기반 거래자의 사적 정보가 포함되지 않은 것들이고, 불균형을 이룬 것은 정보기반 거래자의 사적 정보가 포함된 것으로 볼 수 있다. 약간의 불균형은 비정보기반 거래자의 랜덤한 거래 행위로도 발생할 수 있으나, 불균형 정도가 크다면 정보기반 거래자에 의한 것일 가능성이 높다. 따라서 각 Bucket의 불균형 정도는 PIN 모형의 α와 δ를 추정할 근거가 될 수 있다.

Volume Bucket을 이용하면 위와 같이 VPIN을 추정할 수 있다. 식 1)의 분자는 정보기반 거래자의 거래 강도를 의미하고, 분모는 전체 거래자의 거래 강도를 의미한다. PIN의 정의는 전체 거래 강도 중에 정보기반 거래자의 강도가 얼마나 되는지를 추정하는 것이다.

식 1)의 분자인 αμ는 근사적으로 식 2)로 나타낼 수 있다. 각 Bucket의 매도 수량 (S)과 매도 수량 (B)의 차이가 클수록 (불균형 정도가 클수록) 정보기반 거래자의 거래 강도 (αμ)가 큰 것이다. α = 0 이라면 S = B 이고 각 Bucket은 균형 상태에 있는 것이다. 물론, 이 식은 직관적으로 만든 근사식이다.

식 1)의 분모는 식 3)으로 나타낼 수 있다. 전체 거래자의 거래 강도는 각 Bucket의 평균  거래 강도 (거래량)이다. 모든 Volume Bucket의 거래량은 동일하므로 식 3)은 상수가 된다. 이 상수를 V라 하면, V는 각 Bucket의 거래량을 의미한다. 이 논리를 사용하면 VPIN을 식 5)로 계산할 수 있다. 시장에서 n, V, S, B를 실시간으로 측정할 수 있으므로, 쉽게 VPIN을 측정할 수 있다.

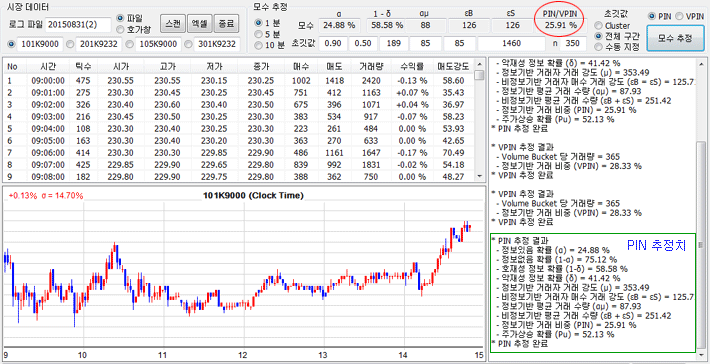
아래 그림은 2015.8.31. (09:00 ~ 15:00) 코스피200 지수 선물의 PIN을 추정한 결과이다. PIN은 단위 시간 당 발생하는 사건의 횟수 (포아송 분포)를 이용한 것이므로 Clock-time based 캔들을 이용한다. 이전 시간에 살펴 본 PIN 추정 방법을 이용하여 PIN을 추정한 결과 25.91% 가 나왔다. 즉 이 날 정보기반 거래자의 참여 비중이 25.91%라는 의미이다.

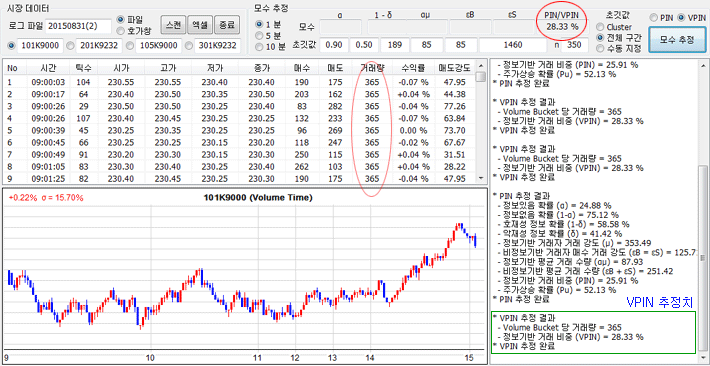
아래 그림은 위와 동일한 데이터를 사용하여 VPIN을 추정한 결과이다. Volume Bucket을 위와 동일한 개수로 표현하기위해 각 Bucket에는 거래량 365개를 부여하였다. 이 Bucket으로 식 5)의 VPIN을 계산한 결과 28.33%가 나왔다. PIN으로 추정한 25.91%와 유사한 결과를 얻었다.

이상으로 VPIN에 대해 살펴보았다. VPIN은 PIN의 대용치 (proxy)로 사용할 수 있고, 변동성의 대용치로 사용할 수도 있다. PIN이나 VPIN이 높다는 것은 결국 변동성이 크다는 것을 의미하므로 VPIN을 변동성의 대용치로 사용할 수 있는 것이다. 위에 소개한 논문에서는 마켓메이커가 VPIN을 이용하여 변동성 위험을 관리할 수도 있다는 것을 언급하고 있다. 이에 대해서는 다음 시간에 살펴보기로 한다.

[출처]38. VPIN 모형|작성자아마퀀트