News & Events
[알고리즘 트레이딩/시장미시구조] 41. 주문 집행 알고리즘 (2) – Almgren의 최적 집행 알고리즘(1)
- 2019년 1월 11일
- Posted by: 인사이트캠퍼스
- Category: 금융/AI/IT 기사

시장미시구조론 (Market Microstructure) – (41)
주문 집행 알고리즘 (2) – Almgren의 최적 집행 알고리즘(1)
이번 시간에는 2000년 Robert Almgren과 Neil Chriss가 “Optimal Execution of Portfolio Transactions”에서 제안한 최적 집행 알고리즘에 대해 살펴본다. 이 알고리즘은 정적 모형 (Static Model)으로 집행 계획을 사전에 미리 설정해 놓고 계획에 따라 집행하는 모형이다. 참고로, 동적 모형 (Dynamic 혹은 Adaptive Model)은 도중에 시장 상황에 맞게 대응하면서 집행하는 모형이다.
Almgren은 총 집행 수량 X를 T 기간 동안 집행할 때 각 구간 별 남은 물량 (잔여 물량)과 집행 물량의 분포를 최적화 하였다. GBM을 따르는 주가 (S)에 영구적 충격을 고려하였고, 실제 체결되는 가격에는 일시적 충격을 고려하였다. 그리고 평가가격 (Benchmark Price)과 실체 체결된 가격으로 거래비용을 계산하고, 거래비용의 기댓값과 분산이 최적 상태가 되도록 각 구간 별 집행 물량을 산정하였다. 평가가격은 집행 시작 시의 주가 (S0)로 설정하고, 각 구간 별 실제 체결 가격들과의 차이를 총 거래비용 (Implementation Shortfall)으로 설정하였다.
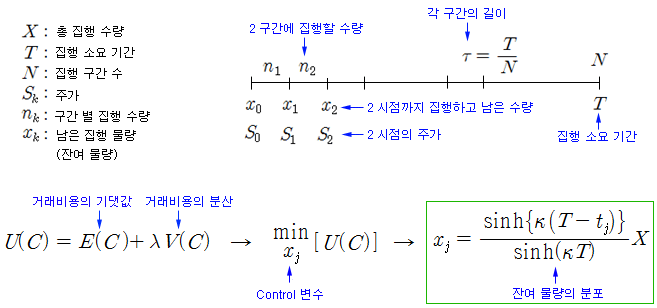
최적화의 원리는 총 비용 (C)에 대한 기댓값 E(C)와 분산 V(C)를 모델링하고, 주어진 분산 수준에서 기댓값을 최소로 하는 잔여 물량 (컨트롤 변수임)의 조건을 찾는 것이다. 이 조건을 찾은 해가 바로 위의 xj 식이다. xj는 잔여 물량으로 j-시점에 집행하고 남은 물량이다 (잔여 물량을 알면 집행 물량을 알 수 있다). 여기서 k (kappa)는 시장 충격계수 (일시적, 영구적), 주가 변동성, 집행자의 위험회피 정도에 의해 결정되는 값이다. k가 클수록 초반에 많은 양의 주문을 집행하고 후반으로 갈수록 적은 양을 집행한다. k가 작을수록 초반부와 후반부에 균등하게 주문을 집행한다.
위의 결과를 엑셀에서 간단히 계산해 보면 아래 그림과 같다. X = 1, T = 10, tj = 0, 1, .., 10 으로 설정하였고, k=0.5와 k=0.2에 대해 계산해 보았다. [그림-1]은 k=0.5일 때 잔여 물량의 분포이다. 집행 초반에 잔여 물량이 큰 폭으로 감소하고, 집행 후반으로 갈수록 감소 폭이 작아진다. 이것은 초반에 집행하는 물량이 많고 후반으로 갈수록 집행 물량이 작아지기 때문이다. [그림-3]은 k=0.2 일 때의 분포이다. k가 작아질수록 초반 집행 비중이 작아지고 구간 별 집행 물량이 점차 균등해 진다. 집행 주체의 변동성에 대한 위험회피 정도가 크면 k도 커진다. 따라서 위험회피 성향이 클수록 초반 집행 물량이 많아진다. 이것은 어느 정도의 시장 충격 비용을 감수하고라도 변동성 위험을 회피하려는 성향 때문이다.
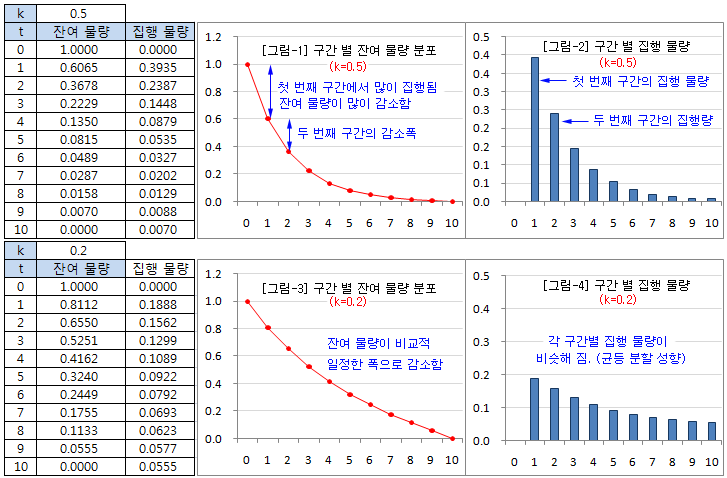
이 모형에서는 S0 (Arrival Price)를 평가가격 (Benchmark Price)으로 설정하였기 때문에 실제 체결 가격이 S0에 가까울수록 거래비용은 감소한다. 따라서 S0에 가까운 집행 초반에 되도록 많은 양을 집행하려는 성향이 있다 (전체를 S0에 체결 시킬 수는 없다). 만약 마지막 종가인 ST를 평가가격으로 설정한다면 (계획 수립 시에는 ST를 알 수 없음), 오히려 후반에 많이 집행하려는 성향이 나타날 것이다. 그리고 0 ~ T 기간 동안의 (일종의) 평균주가 (VWAP이나 TWAP)를 평가가격으로 사용한다면 구간별로 균등하게 집행하려는 성향이 나타날 것이다. 사실, 집행 알고리즘은 평가가격을 어느 수준으로 설정하느냐에 따라 최적 행위가 다르게 나타난다. 평가가격을 어느 가격으로 할 것인가는 기술적 사항이라기보다는 집행 주체의 정책적 사항 (Management 사항)이라 할 수 있다. 즉, 평가가격 설정 정책에 따라 최적 행위는 달라진다.
이제 위의 최적 알고리즘의 해를 얻는 과정에 대해 살펴본다. 식 1)은 잔여 물량으로 앞으로 집행해야 할 수량이다. 식 2)는 주가 모형으로 GBM 과정에 영구적 충격을 포함시켰다 (매도 집행임. 하락 충격을 받음). 일시적 충격은 집행 시 일시적으로 나타났다 사라지는 것이므로 다음 구간의 주가에는 영향을 미치지 않는다. z는 GBM 모형의 확률변수로 평균=0, 분산=1인 표준정규분포를 따른다. 식 3)은 k 구간에서 집행 물량이 일시적 충격을 받은 상태에서 실제 체결되는 가격이다.

식 4) ~ 6)은 각 구간 별로 집행되는 수량과 실제 체결되는 가격을 곱한 것으로 실제 집행한 총 금액 (W)이고, 식 7)은 거래비용인 Implementation Shortfall 이다. 거래비용을 구했으므로 식 8), 9)와 같이 거래비용에 대한 기댓값과 분산을 구할 수 있다.
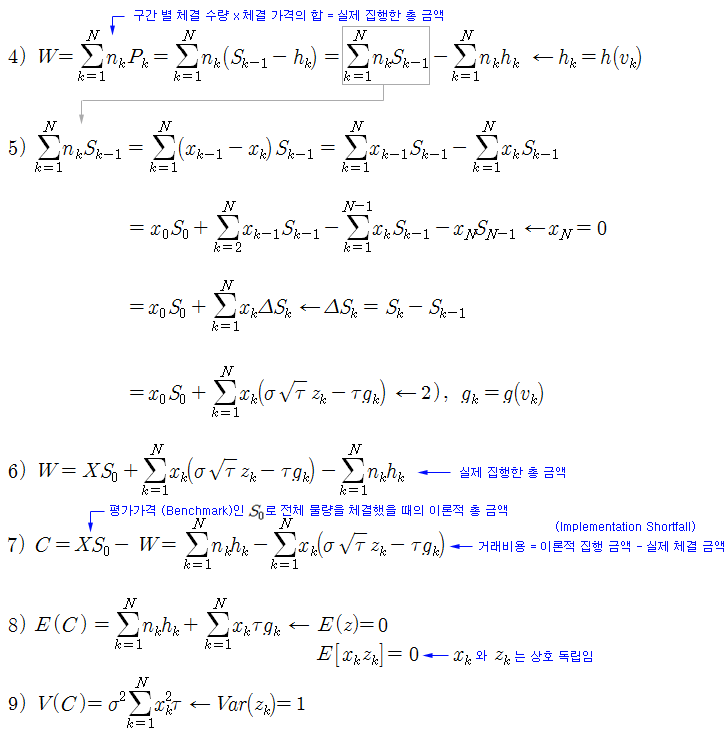
식 8)에서 g와 h를 선형 함수로 가정하여 E(C)를 완성해 보면 식 10) ~ 식 17)의 과정이 된다. 그러면 최종적으로 거래비용에 대한 기댓값과 분산을 식 17)과 18)로 표현할 수 있다.
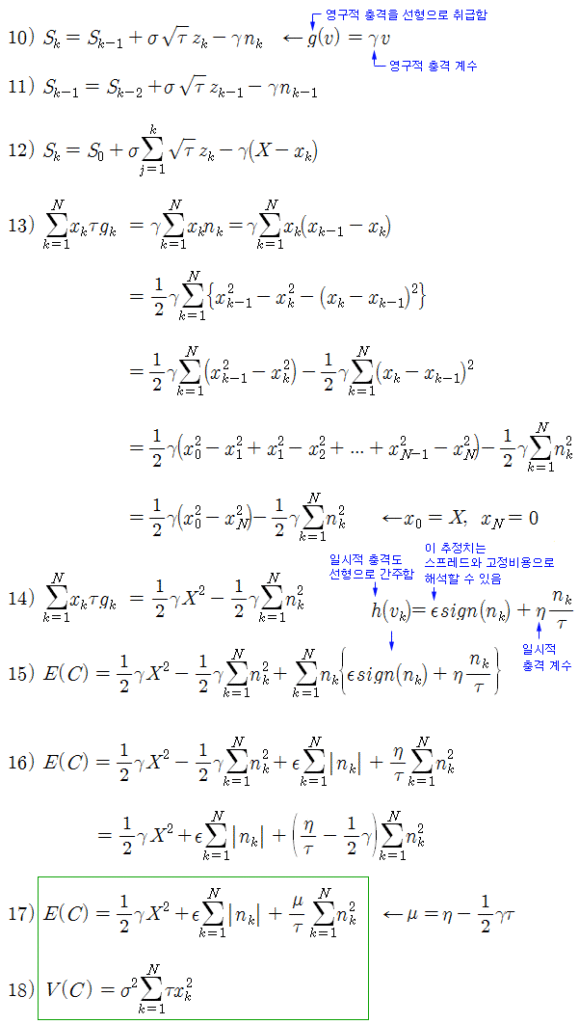
계산이 가능한 형태로 기대비용의 기댓값과 분산을 구했으므로, 라그랑지 승수법에 의해 최적의 해를 구할 수 있다. 식 20)은 잔여 물량에 대한 최적 분포이며, 잔여 물량이 이 분포를 따르도록 구간 별로 집행 계획을 수립할 수 있다. (식 19)에서 20)으로 넘어가는 과정은 생략)
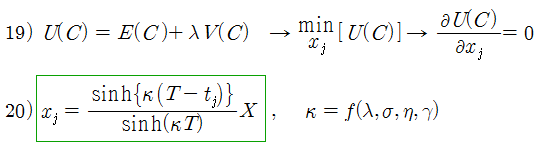
만약 각 구간 별로 균등 분할하여 집행한다면 E(C)는 최소가 되지만 T가 긴 경우 V(C)는 증가할 것이다. 이것은 Timing Risk와 Opportunity Cost가 증가하기 때문이다. 반대로 초기에 전체 물량을 한꺼번에 집행한다면 V(C) = 0 으로 최소가 되지만 시장 충격 비용은 증가할 것이다. 따라서 최적 집행 알고리즘은 이 두 경우의 사이에서 결정될 것이다. 식 20) 이 바로 두 경우의 사이에서 결정된 최적 알고리즘이다.
여기까지가 논문을 이해하기 위한 첫 번째 단계이다. 다음 시간에는 논문의 내용을 조금 더 살펴보기로 한다.

