News & Events
[알고리즘 트레이딩/시장미시구조] 42. 주문 집행 알고리즘 (3) – Almgren의 최적 집행 알고리즘(2)
시장미시구조론 (Market Microstructure) – (42)
주문 집행 알고리즘 (3) – Almgren의 최적 집행 알고리즘(2)
이전 시간에 살펴본 Almgren 모형에 대해 몇 가지 중요한 의미를 살펴본다. Almgren은 집행 시 발생하는 총 비용인 Implementation Shortfall (C)의 기댓값 E(C)와 분산 V(C)를 계산한 후 잔여 물량 (xj)의 최적 분포를 계산해냈다. 최적화 방법은 감내할 수 있는 수준의 변동성 위험을 V(C)* 로 제한해 놓고 비용의 기댓값 E(C)를 최소화 한다 (식 1)의 좌변). 이 방법은 식 1)의 우변을 푸는 문제와 동일하다. λ가 클수록 V(C) 항에 더 큰 penalty가 부여되므로 감내할 수 있는 위험 수준이 높게 잡힌다. 따라서 λ는 위험회피 성향의 크기가 된다. 즉, λ > 0 이면 위험회피 집행자이고, λ = 0 이면 위험중립 집행자가 된다. 그리고 λ < 0 이면 위험선호 집행자가 된다 (최적해가 존재하지 않음).
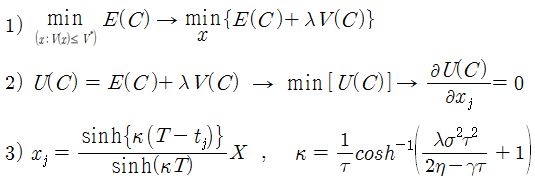
위험중립 집행자 (λ = 0)의 경우 잔여 물량의 최적 분포 (xj)가 어떻게 되는지 살펴보자. λ = 0 이면 식 3)에서 k = 0 이 된다 (식 4). k=0 이면 최적 xj는 X*(T-t)/T 가 된다 (식 5). 즉 xj는 tj에 대한 직선의 방정식이 된다 (식 6). tj 와 xj의 관계를 그려보면 아래 그림의 빨간색 직선이 된다. 따라서 위험중립 집행자의 잔여 물량은 선형으로 감소한다. 이것은 구간별 집행 물량이 균등하다는 것을 의미한다 (식 7). λ = 0 은 식 1)에서 위험에 대한 penalty를 부여하지 않으므로, 시장 변동성은 고려하지 않고 오직 E(C)만 최소로 하겠다는 의미이며, 구간 별로 X/N 씩 분할하여 집행하면 위험중립자의 최적 행위가 되는 것이다.
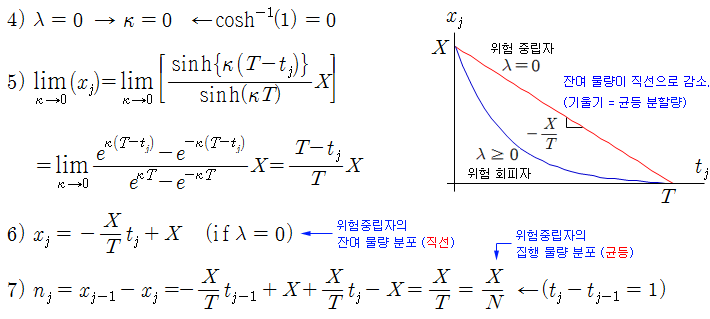
반면에 위험회피자 (λ > 0)의 잔여 물량은 파란색 곡선으로 감소한다. 향후 발생할 위험에 대비해서 초반에 많은 물량을 집행하고, 시간이 지날수록 조금씩 집행한다. 위험회피 성향이 강할수록 더 공격적으로 집행한다. λ는 위험회피 성향의 의미도 있고, 공격성향 (Aggressiveness)의 의미도 갖는다.
이번에는 k (kappa)의 의미를 살펴보자. 식 8)에서 xj 는 j-시점 이후에 집행해야할 수량 (잔여 물량) 이고 X는 총 집행 물량이므로 단위는 모두 수량이다. 따라서 kT 와 ktj 는 단위가 없는 수치이므로 k의 단위는 시간의 역수가 된다. k의 역수를 식 9)로 정의하면 θ의 단위는 시간이 된다. 여기서 θ는 잔여 물량이 소진되는 시간 (Half-life, 반감기 같은 개념임)을 의미한다.
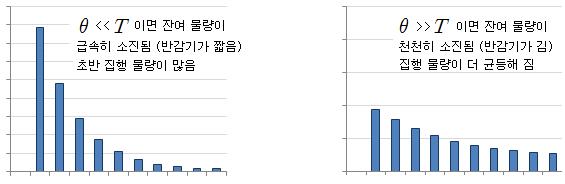
θ가 총 집행 시간인 T에 비해 작다면 잔여 물량은 급속히 감소할 것이다. 즉, 초반에 집행되는 물량이 많아진다. 반면에 θ가 T에 비해 길면 잔여 물량이 천천히 소진된다. 즉, 구간 별로 집행되는 물량이 더 균등해 진다.
Almgren 논문에 의하면 k는 주가 변동성 (σ), 시장 충격계수 (η, γ), 집행자의 위험회피 성향 (λ)의 함수이다 (식 3)의 k). σ, η, γ 는 모두 시장 데이터로부터 추정해야할 값들이다. 즉, 주어진 값들이다. 따라서 k는 집행자의 위험회피 성향 (λ)에 따라 달라진다.
또한 이 식에서 주목할 것은 k는 T와는 무관하다는 것이다. 즉, 집행자는 집행 기간과는 상관없이 오직 위험회피 성향에 따라 집행 물량을 결정한다는 것이다. 집행 기간이 아무리 길더라도, 집행 초기 주가 (Arrival Price)를 Benchmark로 설정하였다면, 위험회피 성향을 가진 집행자는 (λ > 0) 초반에 많은 물량을 집행하려 한다는 것을 의미한다.
k는 위험회피 성향에 따라 달라지고, 두 관계를 그려보면 [그림-1]과 같다. 위험회피 성향이 커질수록 k는 증가한다. 위험회피 성향이 커질수록 k는 증가하고, θ는 감소하므로 잔여 물량의 소진 속도가 빨라진다.
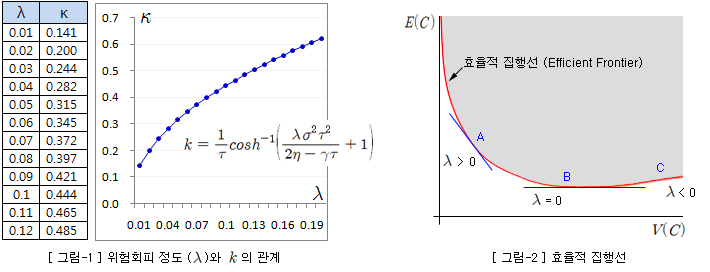
[그림-2]는 위험회피 성향에 따른 효율적 집행선을 그린 것이다. 이 그림은 시장에서 추정된 σ, η, γ를 고정하고, 위험회피 성향을 변경해 가면서 E(C)* 와 V(C)* 를 계산하면 그릴 수 있다. 그림의 빨간색 곡선은 모두 최적한 지점이다. 그리고 λ는 효율적 집행선의 (음의) 기울기에 해당한다.
위험회피 집행자 (λ > 0)는 A-지점을 최적점으로 판단할 것이고, 위험중립 성향을 가진 집행자는 (λ = 0) B-지점을 선택할 것이다. 그리고 위험선호자는 (λ < 0) C-지점을 선택할 것이다. 초기 주가를 Benchmark로 설정한다면, 위험회피자는 초기에 많은 물량을 집행할 것이고, 위험중립자는 균등하게 분할 (X/N 씩)하여 집행할 것이다. 그리고 위험선호자는 초반에 조금 집행하고, 후반으로 갈수록 집행 물량을 늘릴 것이다 (향후 변동성을 즐김).
여기까지 Almgren 논문의 Section 2까지 내용을 살펴보았다. 논문의 나머지 Section에도 유익한 정보가 많이 있지만, 본 블로그에서는 여기까지만 다루어 보기로 한다. 다음 시간에는 VWAP을 Benchmark로 설정하였을 때의 최적 알고리즘에 대해 살펴보기로 한다.
